Если обозначим Vm ρ – плотность газа, то
|
|
|
P |
m |
RT RT. |
|
|||
|
|
|
|
|
|||||
|
|
|
|
V |
|
|
|
|
|
|
Если |
|
рассматривать |
|
смесь |
газов, |
|||
заполняющих объём V при температуре Т, тогда, |
|||||||||
парциальные |
давления, |
можно найти, |
как: |
||||||
P m1RT |
, |
P m2 RT , ….. |
P mn RT |
|
|||||
1 |
1V |
|
2 |
2V |
|
n |
nV |
|
|
|
|
|
|
|
|
||||
31
Согласно закону Дальтона: полное давление смеси газа равно сумме парциальных давлений всех газов, входящих в смесь
P = P1 + P2 + … + Pn
Отсюда, с учетом вышеизложенного, можно
записать |
|
|
|
m2 |
|
mn |
|
|
|
|
|
|
|
||||
|
m1 |
|
... |
|
RT |
|||
|
|
|
||||||
|
PV |
|
|
|
|
|||
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
n |
|
|||
– это уравнение Менделеева-Клапейрона для
смеси газов.
32
33
Пример1.
Баллон содержит газ при 27°С и давлении 200 кПа. Каково будет давление (в кПа), если из баллона выпустить 80% газа и охладить его до 12°С?
Дано: t1 = 27°С, Т1 = 300К; р1= 200 кПа = 2 105Па; t2 = 12°С, Т1=285К; =0,8; m2 = 0,2m1.
Найти: р2.
34
Так как масса газа в баллоне меняется, то начальное и конечное состояния газа в баллоне нельзя связывать объединенным газовым законом (или уравнением изохорного процесса). Нужно для каждого состояния
записать |
уравнение |
|
Клапейрона-Менделеева |
||||
|
p1V |
m1 |
|
, |
p2V |
m2 |
|
|
|
||||||
|
|
M |
|
|
|
M |
|
и, поделив эти уравнения друг на друга, найти конечное |
|||||||
давление |
|
|
|
|
|
|
|
и, поделив эти уравнения друг на друга, найти конечное давление
35
p1V |
|
|
|
|
M |
|
|
||
m1RT1 |
|
|
, |
||||||
p2V |
|
||||||||
|
M |
|
0,2m1RT2 |
||||||
|
|
p1 |
|
|
|
|
|
|
|
|
|
|
|
T1 |
, |
|
|
||
|
|
p2 |
|
|
|
|
|||
|
|
|
0,2T2 |
|
|
|
|||
p2 0,2 p1 T2 , T1
p2 0,2 2 105 300285 38 103 Па 38 кПа .
Ответ: p2 = 38 кПа
36
Пример 2.
Определите минимальный объем наполненного водородом шара, который может поднять человека массой 70 кг на высоту 100 м за время 30 с. Общая масса оболочки шара и корзины 20 кг. Принять g = 10 м с2, плотность воздуха и водорода соответственно равными 1,3 кг м3 и 0,1 кг м3. Сопротивлением воздуха пренебречь. Ответ представьте в единицах СИ и округлите до целого числа.
Дано: 0 = 0, m1 = 70 кг, h = 100 м, t = 30 с, m2 = 20 кг, g = 10 м с2, возд = 1,3 кг м3, вод = 0,1 кг м3
Найти:
Vmin.
37
mчa mш a mH a FA mч g mш g mH g
Полученное выражение запишем в проекции на ось y:
mчa + mшa + mНa = FA – mчg – mшg - mНg.
38
(mч + mш)a + mНa = вgV – (mч + mш)g - mНg.
(mч + mш)a + НVa = вgV – (mч + mш)g - НVg.
НVa - вgV + НVg = - (mч + mш)a - (mч + mш)g.
V( вg - Нa - Нg) = (mч + mш)a + (mч + mш)g.
V( вg - Нa - Нg) = (mч + mш)(a + g).
(mч mш )(a g) V = g(ρв ρН ) ρН a .
В полученном выражении остается неизвестным ускорение, с которым шар поднимается вверх. Найти ускорение можно из уравнения движения шара.
39
|
h 0t |
|
at2 |
|
at |
2 |
. |
|
||||||||||||
|
|
2 |
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Тогда ускорение шара |
|
|
|
|
|
2h |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
a t2 . |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
(m m )( |
2h |
g) |
|
|
|
||||||||||||
|
|
|
|
|
|
|||||||||||||||
Vmin |
ч |
|
|
|
ш |
|
|
t2 |
|
|
|
|
|
|
|
|
||||
g(ρ |
в |
ρ |
Н |
) ρ |
Н |
2h |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
|
|
|
|||||
|
|
|
|
2 100 |
|
|
|
|
|
|
|
|
|
|
. |
|
||||
|
|
90 ( |
|
10) |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
900 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
||
Vmin |
|
|
|
|
|
|
|
|
|
|
|
77 (м |
) |
|||||||
|
|
|
|
|
|
|
|
|
|
2 100 |
||||||||||
10(1,3 0,1) 0,1 |
900 |
|
|
|
|
|||||||||||||||
Ответ: Vmin = 77м3
40
Пример 3.
Два сосуда наполнены одним и тем же газом под давлением 4 105 Па и 9 105 Па массой 0,2 кг и 0,3 кг соответственно. Сосуды соединяют трубкой, объемом которой можно пренебречь по сравнению с объемами сосудов. Найдите установившееся давление в сосудах, если температура газа в них была одинакова и после установления равновесия увеличилась на 20%. Ответ представьте в атмосферах (1 атм = 105 Па) и округлите до десятых.
Дано: p1 = 4 105 Па, p2 = 9 105 Па, m1 = 0,2 кг, m2 = 0,3 кг, T = 1,2 T, 1 атм = 105 Па
Найти: p.
41
Установившееся давление в сосудах можно определить из закона Дальтона:
р = р 1 + р 2, где р 1, р 2 – парциальные давления газа. Эти давления
определяем из уравнения Клапейрона – Менделеева: p (V1 V2) Mm RT
p mRT , M V1 V2
где Т - температура газа после соединения сосудов трубкой, p - парциальное давление, т.е. давление, которое создается газом, если бы он один занимал весь объем.
42
Подставим выражение в закон Дальтона:
|
m1RT |
|
m2 RT |
|
p |
|
|
|
. |
M V1 V2 |
M V1 V2 |
|||
Учитывая условие задачи, согласно которому T = 1,2 T,
уравнение для давления примет вид:
p |
1,2m1RT |
|
1,2m2 RT |
|
1,2RT |
(m1 m2). |
M V1 V2 |
M V1 V2 |
M V1 V2 |
Объемы V1, V2 выразим также из уравнения Клапейрона –
Менделеева, которое записано для случая, когда сосуды еще не соединены трубкой.
43
V mRTpM ,
Тогда
p |
1,2RT |
(m m ) |
|
|
|
1,2RT(m1 |
m2) |
1,2(m1 m2) . |
|||||||||
M V1 V2 |
|
|
|
|
m RT |
||||||||||||
|
1 |
|
2 |
|
|
|
m RT |
|
m1 |
|
m2 |
||||||
|
|
|
|
|
|
|
|
M |
1 |
2 |
|
p1 |
p2 |
||||
|
|
|
|
|
|
|
|
|
|
|
p M |
|
p |
M |
|
||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
p |
1,2(0,2 0,3) |
|
|
7,2 105 |
Па 7,2 атм . |
|
|
|||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
0,2 |
|
0,3 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
105 |
9 105 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||
Ответ: р = 7,2 атм
44
Пример 4. Идеальный одноатомный газ массой 1 кг с молярной массой 4 г/моль нагревают так, что его температура, пропорциональная квадрату давления, возрастает от 300 К до
600 К. |
Определите |
работу, |
совершенную |
газом. |
Универсальная газовая постоянная |
8,31 Дж/(моль К). Ответ |
|||
представьте в килоджоулях и округлите до целого числа.
Дано: m = 1 кг, M = 4 г/моль = 4 10-3 кг/моль, Т = k p2, T1 = 300 К, T2 = 600 К, R = 8,31 Дж/(моль К), i = 3.
Найти: А.
45
Работу, совершенную газом удобнее найти графически. Известно геометрический смысл работы. Она представляет собой площадь фигуры под графиком в pV – координатах. Для этого нужно построить этот график, то есть определить зависимость p = f(V). Для этого запишем уравнение Клапейрона – Менделеева:
pV = RT.
По условию задачи
Т = k p2,
следовательно,
pV = Rkp2 |
|
V = Rkp, |
где , R и k – постоянные величины, т.е. V p. Тогда график зависимости p = f(V) будет выглядеть следующим образом:
46
При t 0, т.е. на бесконечно малом участке траектории перемещение совпадает с траекторией ( s = r).
В этом случае мгновенную скорость можно выразить через
Фигура между графиком и осью х представляет собой трапецию. Значит, работа численно равна площади трапеции.
Sтрап a 2 b h,
47
то есть |
|
|
|
|
|
А |
p1 p2 |
|
(V V ), |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|||||||
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
p |
|
k , |
|
|
|
V Rkp |
Rk |
|
|
k . |
|
||||||||||||
|
|
|
T1 |
|
|
|
T2 |
|
|
|
|
|
|
|
|
|
|
|
νRk |
|
|
|
|
|
|
|||
|
|
|
|
|
|
(νRk T2 |
|
|
|
T1 ) |
( T2 |
T1 |
|
|||||||||||||||
A |
k |
|
|
|
k |
νRk |
) |
|||||||||||||||||||||
|
|
2 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
k |
2 |
|
k |
|
k |
|
|||||
|
mR |
|
(T2 |
T1) |
|
1 8,31 |
|
(600 300) 312 кДж . |
||||||||||||||||||||
2M |
2 4 10 3 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Ответ: А = 312 кДж
48
Пример 5.
По газопроводной трубе идет углекислый газ CO2 под
давлением 3,92 105 Па при температуре 280 К. Какова средняя скорость движения газа в трубе, если через поперечное сечение трубы, равное 5 см2, за время 10 мин протекает газ массой 20 кг? Универсальная газовая постоянная 8,31 Дж/(моль К), молярная масса углекислого газа 44 г/моль. Ответ представьте в единицах СИ и округлите до целого числа.
Дано: CO2, p = 3,92 105 Па, T = 280 К, s = 5 см2 = 5 10-4 м2, t = 10 мин = 600 c, m = 20 кг, R = 8,31 Дж/(моль К),
M = 44 г/моль = 44 10-3кг/ моль
Найти: ср.
49
Средняя скорость - это весь путь нужно разделить на все
время. |
|
|
|
l |
|
||
|
|
|
|
ср t . |
|
||
Путь – это то расстояние, которое газ проходит по трубе. |
|||||||
|
|
|
V = sl |
|
V |
|
|
|
|
|
|
|
|
l s . |
|
Запишем для газа уравнение Клапейрона – Менделеева. |
|||||||
pV |
m |
|
RT |
|
mRT |
|
|
|
|
V Mp . |
|
||||
M |
|
|
|||||
Теперь найдем среднюю скорость движения газа в трубе: |
|||||||
|
|
|
ср l |
V |
mRT . |
|
|
|
|
|
|
t |
tS |
tSMp |
|
ср |
|
|
|
20 8,31 280 |
9 м / с . |
||
|
|
||||||
600 5 105 |
44 10 3 3,92 105 |
||||||
Ответ: ср = 9 м/с
50
Пример 6.
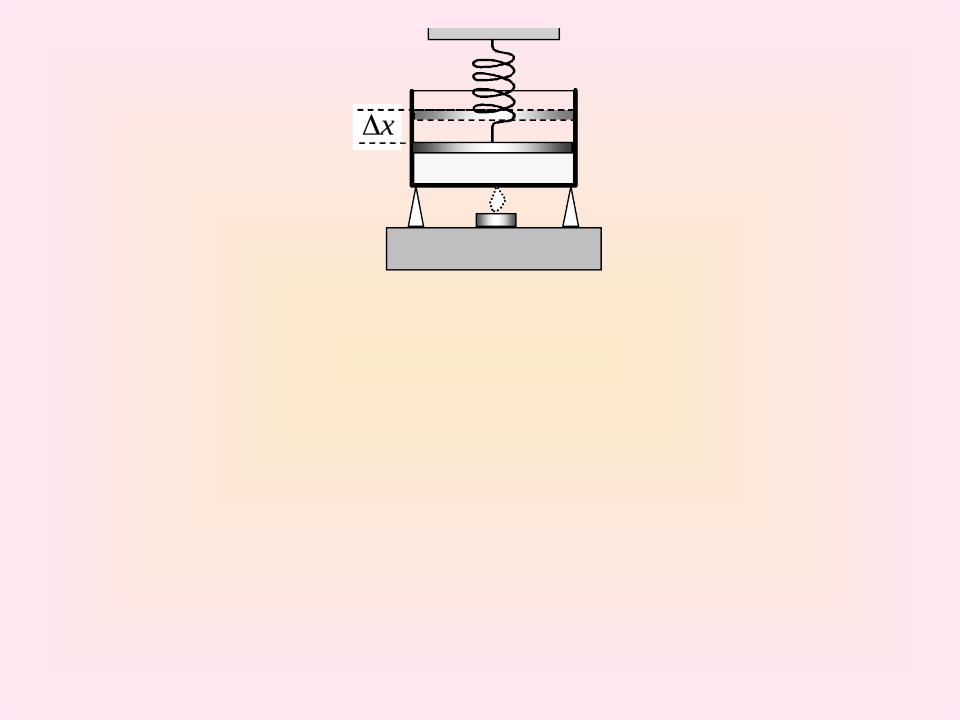
Цилиндр с поршнем содержит газ. Сверху поршень прижат идеальной пружиной. Цилиндр начинают нагревать (см. рисунок). Объем газа изменяется от V1 до V2, а давление от р1 до р2. Определите совершаемую при этом работу газа. Вычисления провести при следующих параметрах:
р1 = 1 105 Па; р2 = 2 105 Па; V1 = 1 л; V2 = 3 л. Ответ
представьте в единицах СИ.
Дано: р1 = 1 105 Па, р2 = 2 105 Па, V1 = 1 л = 10-3 м3, V2 = 3 л = 2 10-3 м3
Найти: А.
51
Так как в системе меняются все параметры: p, V и Т, то работу газа удобнее рассчитать графически (см. предыдущую задачу). По определению давление определяется формулой:
p Fs Fупр = ps.
Но по закону Гука сила упругости определяется следующим выражением:
Fупр = k x.
52
|
|
|
ps = k x |
p |
k x |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
где x – перемещение поршня, которое можно определить через |
|||||||||||||||||||||||||||||||||||||||||||||||
объем. |
|
|
V = s x |
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
x s . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
p k x |
k V |
const V, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
s |
|
s2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то есть давление газа в цилиндре |
|
p |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||||||||||
изменяется |
пропорционально |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
объему: p V. |
|
|
|
p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда в pV – координатах график |
|
p1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
будет |
выглядеть |
аналогично |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sтр |
|
V |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
графику, |
|
представленному |
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
предыдущей |
задаче. Тогда работу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V1 |
|
|
|
|
|
|
|
|
|
V 2 |
||||||||||||||||||
определим через площадь трапеции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
53
A sтр a b h,
2
A p1 p2 V2 V1 .
2
A 105 2 105 3 10 3 10 3 300 Дж . 2
Ответ
54
Пример 7. Найдите число молекул водорода в 1 см3, если давление равно 200 мм.рт.ст., а средняя квадратичная скорость молекул при данных условиях 2400 м/с.
Дано:
V = 1 м3 
p= 200 мм.рт.ст. = 200 133.3 Па
< кв> = 2400 м/с
k = 1,38 10-23Дж/К R = 8,31 Дж/моль К
Найти: n.
55
Решение: Искомая величина может быть найдена из соотношения
р = nkT.
n kTp .
Средняя квадратичная скорость равна
кв 3RT . M
Отсюда температура
T кв 2 M .
3R
56
Окончательно получаем выражение для п
n p 3R .
кв 2 M k
n |
200 133 3 8,31 |
|
4 1024 м 3 . |
||||||
|
|
|
|
|
|
|
|
||
2400 |
2 |
2 |
10 |
3 |
1,38 |
10 |
23 |
||
|
|
|
|
|
|||||
Ответ: n = 4 1024 м-3
57
Пример 8. Средняя квадратичная скорость молекулы углекислого газа при давлении р = 105 Па равна 628 м/с. Определите среднюю длину свободного пробега молекул < >.
Дано:
М = 44 10-3 кг/моль
< кв> = 628 м/с р = 105 Па
NA = 6,03 1023 моль-1 d = 4 10-10 м
Найти: < >.
58
Решение. Средняя длина свободного пробега |
||||
молекул |
1 |
, |
||
|
|
|||
|
|
|
||
|
|
d 2n |
||
2 |
||||
где d - эффективный диаметр молекул; п –
концентрация.
n kTp .
Средняя квадратичная скорость
|
|
|
|
кв |
2 M |
|
|
кв |
3RT |
. |
T |
. |
|||
M |
3R |
||||||
|
|
|
|
||||
Учтем, что
59
|
|
|
|
|
k |
|
R |
, |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
NA |
|
|
|
||||
Тогда |
|
|
|
|
кв 2 M |
|
|||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
. |
|
|||||
|
|
3 |
|
|
d 2pNA |
|
|||||||||
|
|
2 |
|
||||||||||||
|
|
6282 |
44 10 3 |
|
|
|
|
82,2 10 12 |
м 82,2 пм . |
||||||
|
|
|
|
16 10 20 |
105 |
||||||||||
3 2 3,14 |
|||||||||||||||
|
|
|
|
|
|||||||||||
Ответ: < > = 82,2 пм
60
Пример 9. Найдите наиболее вероятную скорость молекул идеального газа.
Дано: m
T
K
Найти: в.
61
Решение. Распределение молекул по абсолютным значениям скорости (распределение Максвелла) выражается формулой
|
m |
|
dN N f d 4 N |
|
|
2 kT |
||
|
||
Введем обозначение: |
|
m a. 2kT
3/ 2 |
e |
|
m 2 2 |
d . |
|
|
2kT |
||
|
|
|
|
|
N = 1
Тогда функция распределения молекул по абсолютным значениям скорости будет иметь вид:
f4 a 3 / 2 e a 2 2 .
62
Чтобы найти наиболее вероятную скорость, нужно взять производную этой функции по скорости и приравнять ее к нулю.
|
|
f |
a 3 / 2 |
- 2a |
3 |
2 . |
|
|
|
|
||||||
|
|
4 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- 2a 3 |
2 0. |
||||||||||||
|
|
|
||||||||||||||
f'( в) = 0; это возможно при |
||||||||||||||||
2 1 |
|
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
2kT |
||||||||
- a в |
1- a в2 0. |
в |
|
a |
|
|
m . |
|||||||||
|
|
|
|
|
Ответ: |
|
|
в |
|
|
2kT |
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
||
63
Пример 10. Внутренняя энергия некоторой массы кислорода равна 3500 Дж. Определите суммарную кинетическую энергию W поступательного движения молекул газа.
Дано:
U = 3500 Дж i = 5
Найти: W.
64
Решение: Внутренняя энергия молекул идеального газа выражается следующим образом:
|
i |
|
m |
(1) |
|
|
|
|
|
|
|
U 2 |
|
M RT, |
|||
|
|
||||
где i - число степеней свободы.
Суммарная кинетическая энергия поступательного движения для N молекул определяется как
W 32 kT N 32 kT Mm NA 32 Mm RT,
где kNA = R.
Из уравнения ( 1 ) находим
65
Mm RT 2Ui .
Тогда
W |
3 |
2U |
3U |
|
3 3500 |
2100 Дж . |
2 |
i |
i |
|
5 |
Ответ: W = 2100 Дж