Сегодня: Thursday, July 4, 2019
Лекции 19, 20
Элементы квантовой механики
Содержание лекции:
•Гипотеза де Бройля
•Свойства микрочастиц
•Соотношение неопределенностей
•Волновая функция
•Уравнение Шредингера
•Квантование физических величин
1. Гипотеза де Бройля
Свет ведет себя двойственным образом – корпускулярно- волновой дуализм.
В 1924 г. Луи де Бройль выдвинул гипотезу об
универсальности дуализма – волновые и одновременно
корпускулярные свойства присущи не только свету, но и веществу:
с любой движущейся частицей связана плоская
монохроматическая волна, распространяющаяся в направлении скорости частицы – волна де Бройля (фазовая волна, волна вещества).
Длина волны де Бройля: |
Частота: |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
v |
E |
|
|
|
p |
|
|
|
|
|
|||
|
|
|
h |
|
|||||
|
|
|
|
|
|
|
|
|
|
р – импульс частицы; Е – ее энергия.
2. Свойства микрочастиц
Микрочастицами называются
•элементарные частицы (как заряженные, так и нейтральные – электроны, нейтроны, фотоны…)
•сложные частицы, состоящие из сравнительно небольшого числа элементарных частиц (ядра, атомы…).
Это особые образования, обнаруживающие как волновые, так и корпускулярные свойства:
-отличие микрочастицы от волны заключается в том, что она всегда обнаруживается как неделимое целое.
-отличие микрочастицы от макрочастицы заключается в том, что к ней не применимо понятие траектории.
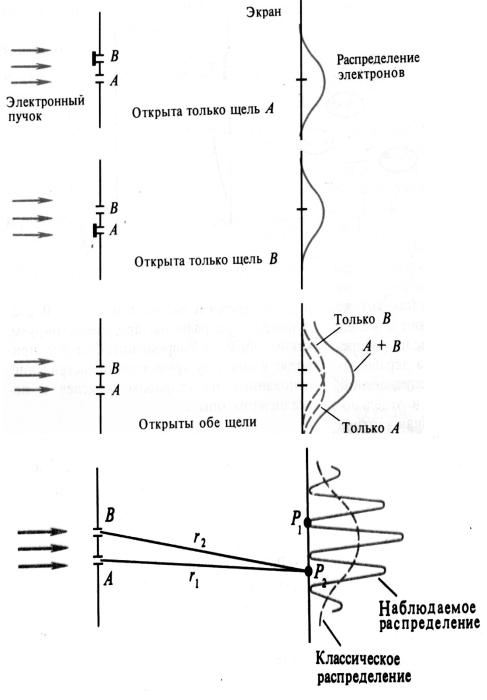
Рассмотрим следующий эксперимент:
узкий пучок моноэнергетических электронов проходит через преграду с двумя узкими щелями:
При поочередном открывании щелей получаются классические кривые распределения электронов;
Если открыть обе щели, распределение электронов не будет наложением двух первых распределений, а будет
аналогична картине, получающейся при наложении двух когерентных световых волн.
На движение электрона влияют оба отверстия, что несовместимо с понятием траектории (электрон должен был бы пройти либо через одну щель, либо через вторую).
Дифракция электронов на щелях
Законы интерференции и дифракции действуют для пучков элементарных частиц также, как для световых волн.
Ни одна макрочастица не может служить прообразом микрочастицы, т.к. с уменьшением размеров начинают проявляться принципиально новые свойства, не обнаруживающиеся у макрочастиц (через отверстие не может пройти полэлектрона).
3.Соотношение неопределенностей
Вклассической механике состояние материальной точки (классической частицы) определяется заданием значений координат импульса, энергии и т.д.
-динамических переменных. Основное соотношение – II закон Ньютона,
при решении которого определяется траектория частицы (координата и импульс определены для каждого момента времени).
Микрообъекту не могут быть приписаны указанные динамические переменные, но:
•информация о микрочастицах получается при наблюдении их взаимодействия с приборами (макроскопическими телами).
•по этой причине результаты измерений выражаются в терминах, разработанных для характеристики макротел, т.е. через значения динамических характеристик. В соответствии с этим измеренные значения динамических переменных приписываются микрочастицам. Например,
говорят о состоянии электрона, в котором он имеет такое-то значение энергии, и т.д.
Для микрочастиц в силу корпускулярно- волновой двойственности их свойств одновременно задать координату и импульс невозможно
Для канонически-сопряженных величин справедливо соотношение неопределенностей Гейзенберга:
A B h2
Произведение неопределенностей значений двух сопряженных переменных не может быть по порядку величины меньше приведенной постоянной Планка – принцип неопределенности Гейзенберга.
Чем меньше неопределенность одной сопряженной величины, тем больше неопределенность другой.
Канонически сопряженными величинами являются:
• Координата и проекция импульса на соответствующую ось:
x px h2
• Энергия и время: |
|
|
|
- определение энергии с точностью E |
E t |
|
h |
||
|
2 |
должно занять интервал времени, |
||
|
|
|
равный, по меньшей мере, t : h/ E |
Дифракция частицы на щели:
Уменьшение неопределенности координаты х сопровождается возрастанием неопределенности компоненты импульса рх
Соотношение неопределенностей указывает, в какой мере возможно пользоваться понятиями классической механики применительно к микрочастицам, в частности, с какой
степенью точности можно говорить о траекториях микрочастиц:
Распишем импульс как произведение массы частицы на ее скорость: h
x vx 2m
- чем больше масса частицы, тем меньше неопределенность ее
координаты и скорости, т.е. с тем большей точностью можно применять к этой частице понятие траектории.
для макроскопических тел их волновые свойства не играют никакой роли; для описания их движения с абсолютной достоверностью можно пользоваться законами классической механики.