Сегодня: четверг 4 Июль, 2019 |
Лекция 6 |
Электромагнитные волны
Содержание лекции:
•Образование свободных электромагнитных волн
•Плоские электромагнитные волны
•Свойства электромагнитных волн
•Стоячие электромагнитные волны
•Энергия электромагнитных волн
1. Образование свободных электромагнитных волн
Пусть в некоторой точке О безграничной проводящей среды создается электрическое поле E
Вотсутствие поддерживающих электрических зарядов
электрическое поле уменьшается, порождая магнитное поле H
Вотсутствие поддерживающих токов магнитное поле r уменьшается, порождая вихревое электрическое поле E1; в точке О электрическое поле обратится в нуль, но возникнет в точке 1 и т.д...
Итак, вместо первоначального электрического поля будут электрические, магнитные поля, взаимно связанные друг с другом и распространяющиеся в пространстве с образованием свободных электромагнитных волн.
Свободные электромагнитные волны |
3 |
2. Плоские электромагнитные волны
Покажем, что существование электромагнитных волн вытекает из уравнений Максвелла:
Запишем их для случая однородной нейтральной (ρ = 0) |
|||||
|
|
r |
0 среды: |
|
|
непроводящей j |
|
||||
r |
r |
D |
|
D |
div D 0 |
rot H j |
t |
t |
|||
|
r |
|
r |
||
|
B |
|
|||
|
|
div B 0 |
|||
rot E |
t |
|
|
|
|
r r |
f x,t |
Рассмотрим случай плоской волны: E, H |
Распишем первую пару уравнений в координатной форме:
r |
|
|
H |
z |
|
|
H y |
|
|
|
D |
|
||
rotx H |
|
|
|
|
|
|
|
0 |
x |
- Dx, Вx не |
||||
|
y |
|
z |
|
||||||||||
|
|
|
|
|
|
|
|
|
t |
зависят от |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
E |
|
|
Ey |
0 |
B |
времени. |
||||||
|
|
|||||||||||||
rotx E |
|
|
z |
|
|
|
|
x |
|
|||||
|
|
|
z |
|
|
|||||||||
|
|
|
y |
|
|
|
|
|
|
t |
|
|||
Расписав вторую пару уравнений в координатной форме, получаем:
Dx |
0 |
|
|
x |
|
- Dx, Вx не |
|
Bx |
0 |
зависят от х. |
|
|
|
||
x |
|
Dx = const |
- обусловлены постоянными |
Следовательно, |
однородными полями, |
||
|
|
Вx = const |
накладывающимися на |
|
|
электромагнитное поле волны |
|
r r
Само поле волны не имеет составляющих вдоль Ох, т.е. E, H Ox
- электромагнитная волна – поперечная.
Будем полагать постоянные поля отсутствующими: Ех = Нх = 0. Остальные компоненты:
Dy Hzt x
Bz Eyt x
Пусть Ey = E, |
Ez = 0 |
Hy = 0, |
Hz = H |
Dz H yt x
By Ezt x
D Ht x
B Et x
- уравнения
Максвелла для одномерного случая
3. Свойства электромагнитных волн
Волновое уравнение для электромагнитной волны:
2 E |
|
1 |
2 E |
|
t2 |
0 0 |
x2 |
||
|
Скорость электромагнитной волны:
v |
1 |
|
1 |
|
1 |
|
c |
|
0 0 |
0 0 |
|
|
|
||||
|
|
|
|
|||||
c |
1 |
|
- скорость электромагнитных волн |
|
0 0 |
||||
|
в вакууме |
|||
|
|
|
|
|
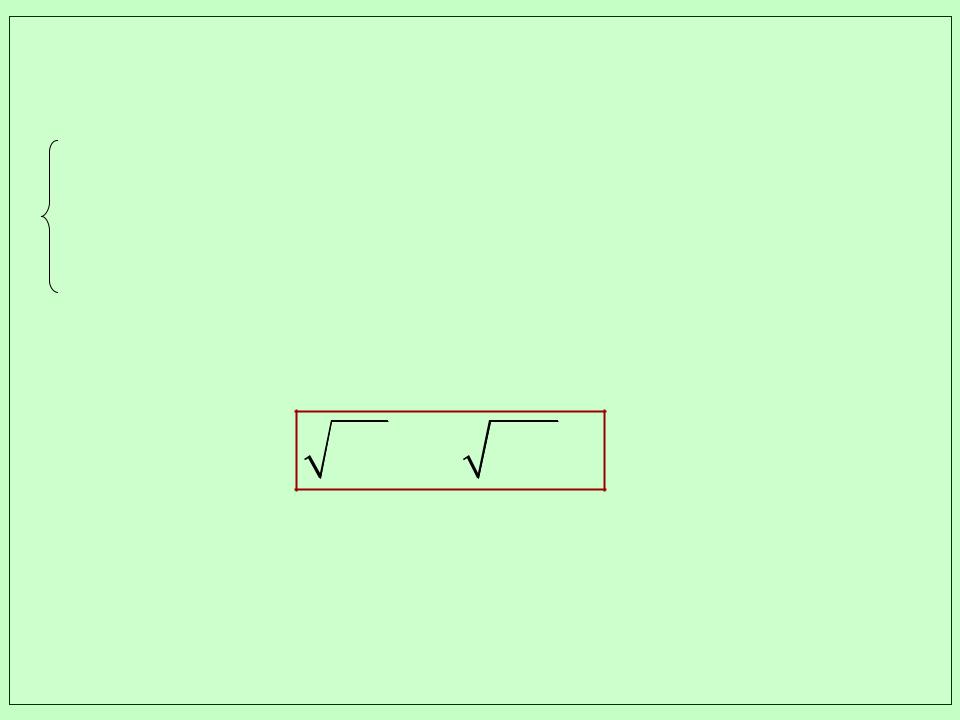
Простейшим решением волнового уравнения являются
монохроматические (синусоидальные) волны:
r |
r |
cos t kx |
Е0, Н0 – амплитуды |
E |
E0 |
||
r |
r |
0 cos t kx |
волны. |
H H |
|
||
Связь между мгновенными значениями напряженностей:
0 E 0 H
Колебания электрического и магнитногоr r векторов происходят синфазно, причем векторы E, H образуют с направлением распространения волны правовинтовую систему.
Распределение электрического и магнитного полей в распространяющейся волне
Изменение поля во времени
10