
Информатика_140800 / 2011-2012-учебный год / 1_семестр / Сам_изуч / Тема_1_2
.pdf
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Государственное образовательное учреждение высшего профессионального образования
«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Представление информации в ЭВМ
(лекции по курсу Информатика для бакалавров направления 140800 )
Преподаватель каф. ЭАФУ
Нагайцева Ольга Викторовна
Томск 2011

системы счисления;
преобразование чисел из одной системы счисления в другую;
основные арифметические операции над двоичными числами;
представление числовой, символьной, звуковой и графической информации в ЭВМ.
2

СИСТЕМА СЧИСЛЕНИЯ |
|
совокупность приемов записи |
|
и наименования чисел |
|
|
|
Непозиционная |
|
Позиционная |
система, в которой цифры не меняют своего |
|
величина числа зависит не только от набора цифр, но и от |
количественного значения при смене позиции в числе |
|
того, в какой последовательности записаны символы, т.е. от |
|
|
позиции, занимаемой цифрой |
|
|
|
3

Число в позиционной системе счисления (CC) с основанием P:
X(p) Xn1Pn1 Xn 2Pn 2 ... X1P1 X0P 0 X 1 P1 X2P2 ... X mP m (1)
где X(p) – запись числа в системе счисления с основанием P; |
n – число разрядов целой части; |
Xi – числа в пределах от 0 до P-1; |
m –число разрядов дробной части. |
Основанием системы счисления (P) называется количество цифр, используемых для записи числа. При этом
сами значащие цифры лежат в пределах от 0 до P–1.
Закодированная запись числа в P-ой CC:
|
|
|
|
|
X(P) Xn 1Xn 2 X1X0 , X 1X 2 X m |
|
|
|
(2) |
|||
Максимальное число целой части числа в |
Минимальное значащее (не равное 0) число |
|
||||||||||
P-ой СС : |
|
|
дробной части числа в P-ой СС: |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R max P n 1 |
|
(3) |
|
Rmin P m |
|
|
(4) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Характеристики широко используемых СС: |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||
|
|
Система счисления |
|
Основание |
Используемые символы |
|
|
|||||
|
|
десятичная |
|
10 |
0 - 9 |
|
|
|
|
|||
|
|
двоичная |
|
2 |
0 -1 |
|
|
|
|
|||
|
|
восьмеричная |
|
8 |
0 - 7 |
|
|
|
|
|||
|
|
шестнадцатеричная |
|
16 |
0 – 9, 10 – A, 11 – B, 12 – C, 13 – D, 14 – E, 15 - F |
|
|
|||||
4

5
Прямой перевод:
Целая часть числа:
1) целая часть числа делится на основание новой CC; |
в этом случае остаток всегда будет меньше |
|
2) делим до тех пор, пока результат не будет равен нулю |
|
основания новой CC, то есть 1 для 2-й СС, |
|
|
|
|
1-7 для 8-й СС и т.д. |
|
3) новое число составляется путем записи полученных |
||
|
|
||
|
остатков от деления в обратном порядке. |
|
|
|
|
|
|
Дробная часть числа:
1) дробная часть числа умножается на основание новой СС; |
|
на 2 (8 или 16) для 2, 8 и 16-й СС |
|
||
|
|
|
2) целая часть результата умножения используется для записи числа, а дробная снова умножается на основание новой СС.
3) умножение продолжается до тех пор, пока дробная часть не станет равной нулю или не будет достигнута требуемая точность перевода.
Обратный перевод: число представляется полином (1) (см. слайд 4) и рассчитывается соответствующая сумма.
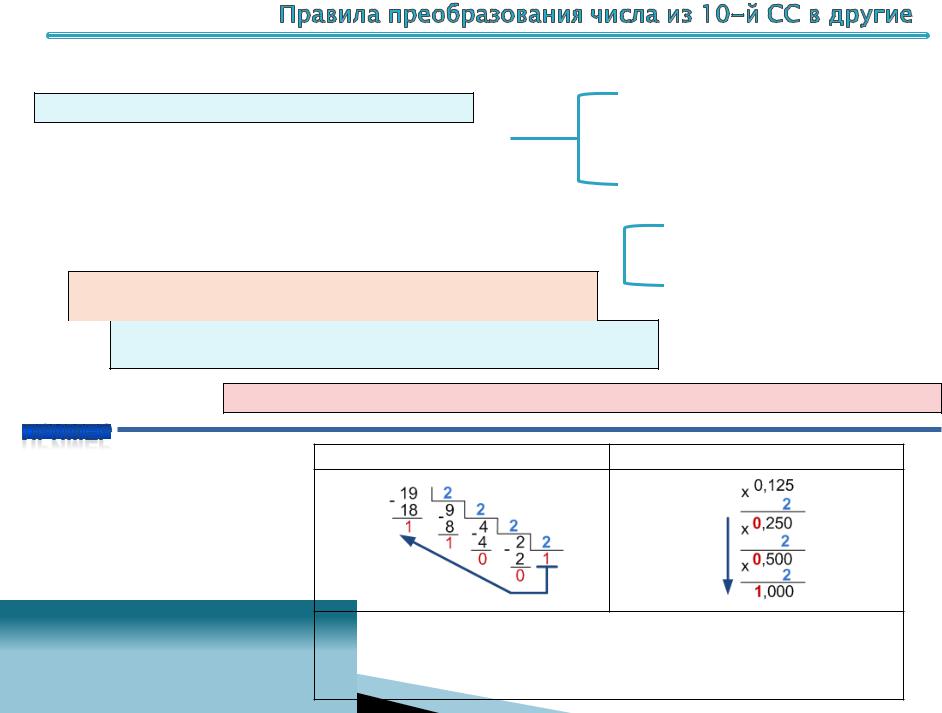
Перевод целой части числа (19): |
Перевод дробной части числа (0,125): |
Переведем десятичное число 19,125(10) в двоичную систему счисления и затем из двоичной обратно.
Результат перевода: 19,125(10) = 10011,001(2) |
|
|
Обратный перевод:1 24 0 23 0 22 1 21 1 2 |
0 0 2 1 0 2 2 1 2 3 19,125 |
6 |
|
|

Прямой перевод:
|
|
|
|
триада – группа из 3-х цифр; |
1) исходное двоичное число разбивается на триады для |
|
|
||
|
|
|
||
8-й СС (тетрады для 16-й СС); |
|
|
тетрада – группа из 4-х цифр; |
|
|
2) затем каждая триада (тетрада) заменяется |
|
|
|
|
соответствующей 8-ой (16-ой) цифрой; |
|
|
|
|
|
|
|
|
3) для целой части числа триады (тетрады) формируются от запятой справа налево, для дробной – слева направо;
4) Недостающие двоичные цифры заменяются 0.
Обратный перевод: |
каждая восьмеричная (шестнадцатеричная) цифра числа заменяется соответствующей |
|
триадой (тетрадой) из двоичных цифр. |
||
|
||
|
|
1)Переведем двоичное число
11101111,1(2) в восьмеричную и шестнадцатеричную СС.
2)Переведем восьмеричное
число |
315(8) |
и |
шестнадцатеричное 3BE,4(16) |
в |
|
двоичную СС. |
|
|
1) Перевод числа 11101111,1 в |
Перевод числа 11101111,1 в 16-ю СС |
8-ю СС |
|
Результат перевода: |
Результат перевода: |
011 101 111,100(2) |
|
357,4(8) |
|
||
2) Перевод числа 315 в 2-ю СС Перевод числа 3BE,4 в 2-ю СС |
||
Результат перевода: |
Результат перевода: |
7

|
0 + 0 = 0 |
Сложение |
0 + 1 = 1 |
|
1 + 0 = 1 |
|
1 + 1 =10 |
|
|
|
0 - 0 = 0 |
Вычитание |
1 - 0 = 1 |
|
1 - 1 = 0 |
|
10 - 1 = 1 |
|
|
|
0 · 0 = 0 |
Умножение |
0 · 1 = 0 |
|
1 · 0 = 0 |
|
1 · 1 = 1 |
|
|
Сложение |
|
+ 1100 (12) |
|
|
||||||
|
|
|
|
110 (6) |
|
|
|
|||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
|
|
10010 (18) |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
-10010 (18) |
|
|
||||||
Вычитание |
|
|
|
|
101 (5) |
|
|
|||
|
|
01101 (13) |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1001 (9) |
|
|||
|
|
|
|
|
|
110 (6) |
|
|
||
Умножение |
|
|
|
|
|
0000 |
|
|
|
|
|
|
|
|
|
1001 |
|
||||
|
|
|
|
|
1001 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
110110(54) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
- |
110110 (54) |
|
|
110 |
|||||
|
|
|
||||||||
|
|
|
1001 |
|||||||
|
|
110 |
(6) |
|
|
|||||
Деление |
|
|
|
|
|
|
|
|
|
|
- |
000110 |
|
|
|
|
|||||
|
|
|
|
|
||||||
|
|
110 |
|
|
|
|
||||
|
|
000 |
|
|
|
|
||||
8

. |
|
|
Формы представления чисел |
|
|
|
|
|
|
|
|
||
С фиксированной точкой |
|
|
|
С плавающей точкой |
||
|
( для чисел по модулю < 1) |
|
|
|
||
|
|
(для целых чисел) |
|
N M PR |
(5) |
|
|
|
|
|
|
||
Общий формат с точкой справа от младшего разряда |
где P – основание системы счисления, |
|||||
|
|
|
|
|||
2n-1 2n-2 |
|
21 |
20 |
M – мантисса, R – порядок числа. |
|
|
Знак |
|
|
|
|
||
.... |
|
. точка |
|
|
|
|
числа |
|
|
|
|
||
|
|
|
|
|
|
|
n -1 n - 2 |
|
1 |
0 |
|
|
|
|
разряды |
|
|
4235,25 |
42,3525 102 |
0, 423525 104 |
|
|
|
|
|
|
|
|
|
|
|
423,525 101 |
4,23525 103 |
|
16 разрядная ячейка для хранения целых со знаком: |
|
|
|
|||
числаЗнак |
214 |
213 |
….. |
|
|
|
20 |
|
|
|||
|
|
диапазон чисел [- 215, + 215 – 1] |
|
1 |
M 1 |
(6) |
||||||
|
|
|
|
|
|
|
|
|
|
P |
|
|
16 разрядной ячейки для хранения целых без знака: |
|
|
||||||||||
2 |
15 |
2 |
14 |
2 |
13 |
.... |
2 |
1 |
2 |
0 |
0,1 M 1 |
|
|
|
|
|
|
для десятичной СС: |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
диапазон чисел [0, 65635] |
|
|
|
|
||||
9

знак |
машинный |
М АН |
Т И С |
С А |
числа |
порядок |
|
|
|
|
1-й байт |
2-й байт |
3-й байт |
4-й байт |
Машинный |
0 |
1 |
2 |
3 |
... |
64 |
65 |
.... |
125 |
126 |
127 |
|
порядок |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
Математический |
-64 |
-63 |
-62 |
-61 |
... |
0 |
1 |
.... |
61 |
62 |
63 |
|
порядок |
|
|
|
|
|
|
|
|
|
|
|
Мр = р + 64 |
(7) |
Мр2 = р2+100 00002 |
(8) |
|
|
|
|
|
|
|
|
где Мр - машинный порядок, а р - математический
10
