Информатика_140800 / 2011-2012-учебный год / 2_семестр / Сам_изучение / Интерполирование сплайнами

Интерполирование сплайнами

Интерполирование многочленами Лагранжа или Ньютона на всем отрезке с использованием большого числа узлов интерполяции часто приводит к плохому приближению, что объясняется сильным накоплением погрешности в процессе вычислений. Для того чтобы избежать больших погрешностей, весь отрезок разбивают на частичные отрезки и на каждом из частичных отрезков приближенно заменяют функцию многочленом невысокой степени (кусочно-полиномиальная интерполяция). Одним из способов интерполирования является интерполирование с помощью сплайн-функций.

Сплайн-функцией или сплайном называют кусочно-полиномиальную функцию, определенную на отрезке и имеющую на этом отрезке некоторое число непрерывных производных.

Интерполяция кубическим сплайном

Пусть на интервале задана непрерывная функция . Введем

и обозначим, .

Сплайном, соответствующим функции и узлам называется функция , удовлетворяющая следующим условиям:

1. на каждом сегменте, функция является многочленом третьей степени;

2. функция , а также ее первая и вторая производные непрерывны на (условия непрерывности);

3. (условия интерполирования).

Построение сплайна (алгоритм интерполирования):

В отличие от интерполяции Лагранжа, когда вся функция аппроксимируется одним полиномом, при сплайновой интерполяции на каждом интервале

На каждом отрезке будем искать функцию в виде многочлена (3.4.1):

(3.4.1)

где - коэффициенты, подлежащие определению.

Коэффициент

Коэффициент, так как .

Коэффициент , так как .

Коэффициент , так как .

Найдем коэффициенты из условий, которым должен удовлетворять сплайн:

1. Условия интерполирования: при этом 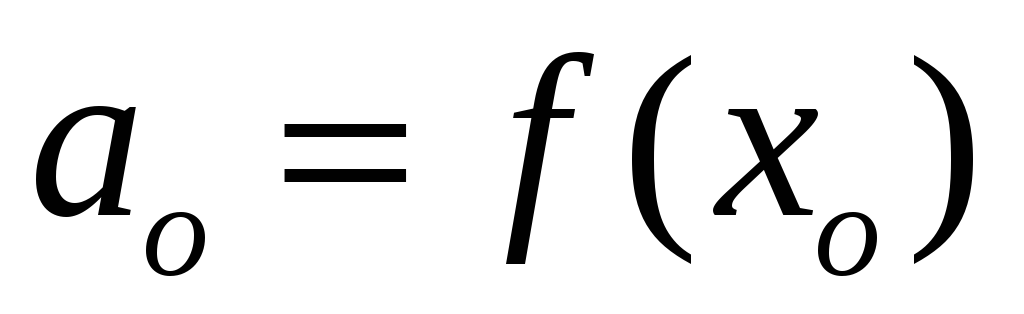и условия непрерывности функции: для каждого приводят к уравнению (3.4.2):

(3.4.2)

Обозначим , перепишем уравнениям (3.4.2) в виде (3.4.3)

(3.4.3)

2. Условия непрерывности первой производной для каждого приводят к уравнениям (3.4.4)

(3.4.4)

3. Условия непрерывности второй производной для каждого приводят к уравнениям (3.4.5):

(3.4.5)

Объединяя уравнения (3.4.3), (3.4.4), (3.4.5) получим систему уравнений относительно неизвестных .

Два недостающих уравнения получают, задавая те или иные граничные условия для . Например, что функция удовлетворяет условиям . Тогда из этого условия получаем недостающие уравнения (3.4.6):

и (3.4.6)

Таким образом, получаем замкнутую систему, разрешив которую относительно коэффициентов кубического сплайна получим эти коэффициенты.

Для решения данной системы хорошо применим метод прогонки. Алгоритм данного метода приведен в Мудров А.Е. Численные методы для ПЭВМ на языках бейсик, фортран, паскаль, 1991 г.