Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Политехнический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Численные методы_решения_алгебраич_уравнений

.doc

Скачиваний:

Добавлен:

30.05.2015

Размер:

294.4 Кб

Скачать

☆

Метод дихотомии или половинного деления

Считаем, что отделение корней уравнения (1.1.1) проведено и на отрезке расположен один корень, который необходимо уточнить с погрешностью .

Метод заключается в следующем:

1) Определяем середину отрезка :

(1.3.1)

2) Затем вычисляем значение функции в ().

3) Далее делаем выбор, какую из двух частей отрезка взять для дальнейшего уточнения корня:

- если левая часть уравнения (1.1.1) есть непрерывная функция аргумента , то корень будет находиться в той половине отрезка, на концах которой имеет разные знаки:

(1.3.2)

4) Далее смещают соответствующую границу в точку .

5) Продолжаем процесс деления как с первоначальным отрезком до тех пор пока не выполнится критерий сходимости.

Критерии сходимости при решении уравнений:

Абсолютное изменение приближения на соседних шагах итерации:

(1.3.3)

Близость к нулю вычисленного значения левой части уравнения (1.1.1):

(1.3.4)

где - заданная погрешность определения корня.

Структурная схема алгоритма

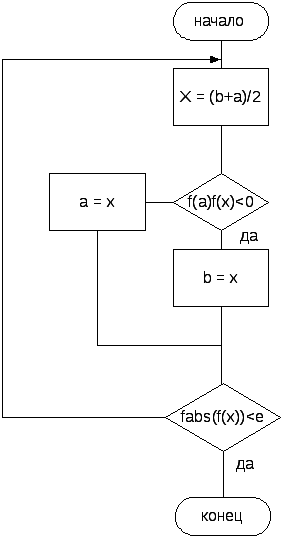
Метод дихотомии позволяет значительно уменьшить объем вычислений по сравнению с графическим методом. Так как за каждую итерацию интервал, где расположен корень, уменьшается в два раза, то через n итераций будет равен . За 10 итераций интервал уменьшится в 2²⁰ примерно в 10⁶ раз.

Метод Ньютона (метод касательных)

Предположим, что графическим методом определено начальное приближение к корню.

В точке вычислим левую часть уравнения (1.1/1) , а также производную в этой точке .

Далее находим следующее приближение к корню как точку, в которой касательная к функции , проведенная из точки пересекает ось абсцисс.

Получим рекуррентное соотношение для пересчета приближения к корню.

Запишем уравнение касательной к точке (1.5.1).

(1.5.1)

Найдем такой , при котором данное уравнение обращается в ноль, получим (1.5.2):

(1.5.2)

Далее данная процедура повторяется.

В общем виде для - шага итерационного процесса последнее соотношение принимает вид (1.5.3

(1.5.3)

С каждой итерацией расстояние между очередным и предыдущим приближениями к корню будет уменьшаться. Процесс уточнения корня закончится тогда, когда выполнится условие (1.5.4)

(1.5.4)

где - заданная погрешность определения корня.

Также критерием окончания итерационного процесса может быть условие (1.5.5):

(1.5.5)

где - заданная погрешность определения корня.

Метод Ньютона обладает высокой скоростью сходимости. Обычно абсолютная точность решения достигается через 5-6 итераций.

Недостатком метода является необходимость вычисления на каждой итерации не только левой части уравнения, но и ее производной.

Можно, несколько уменьшить скорость сходимости, если ограничится вычислением производной только на первой итерации. Таким образом, получаем модифицированный метод Ньютона.

Модифицированный метод Ньютона

Алгоритм поиска корня уравнения (1.1.1) повторяется практически также как в искомом методе Ньютона с единственным исключением, производная вычисляется лишь на первой итерации и далее это значение используется на следующих итерациях. Рекуррентное соотношение для уточнения корня будет выглядеть так (1.6.1):

(1.6.1)

1.7 Метод секущих

Если итерации и расположены достаточно близко друг к другу, то производную в алгоритме Ньютона можно заменить ее приближенным значением в виде отношения приращения функции к приращению аргумента .

Тогда рекуррентное соотношение для уточнения корня на к - шаге примет вид (1.7.1):

(1.7.1)

Условия окончания итерационного процесса:

Абсолютное изменение приближения на соседних шагах итерации (1.7.2):

(1.7.2)

Близость к нулю вычисленного значения левой части уравнения (1.7.3):

(1.7.3)

где - заданная погрешность определения корня.

Для того чтобы начать итерационный процесс. Необходимо задать два начальных приближения и .

Затем каждое новое приближение к корню получаем по формуле (1.21). Заканчиваем процесс уточнения корня, если выполняются условия окончания итерационного процесса (1.7.2), (1.7.3).

Метод секущих уступает по скорости сходимости методу Ньютона, однако не требует вычисления производной левой части уравнения (1.1.1).

По алгоритму метод секущих близок к методу хорд, однако в отличие от последнего начальные приближения могут располагаться как с разных сторон от корня, так и с одной стороны.

1.8 Метод простых итераций

Предположим, что уравнение (1.1.1) при помощи некоторых тождественных преобразований приведено к виду (1.7.4):

(1.7.4)

Пусть известно начальное приближение к корню , тогда подставим его в правую часть уравнения (1.7.4) и получим новое приближение (1.7.5):

(1.7.5)

Затем аналогичным образом получим и т.д.:

(1.7.6)

Заметим: тот факт, что корень уравнения , означает, что есть абсцисса точки пересечения графика с прямой .

Необходимо установить, при каких условиях итерационный процесс будет сходиться к корню уравнения .

Рассмотрим процесс графически (рисунок 1).

Рисунок 1

Из графиков видно, что при и при возможны как сходящиеся, так и расходящиеся итерационные процессы.

Скорость сходимости зависит от абсолютной величины производной функции . Чем меньше вблизи корня, тем быстрее сходится процесс.

Установим теперь критерий сходимости математически.

Будем считать, что в итерационной формуле (1.7.6)

(1.7.7)

где , - отклонения k и k+1приближения к корню. Если процесс уточнения осуществляется вблизи корня , то функцию можно приближенно представить двумя членами ряда Тейлора. Тогда итерационная формула (1.7.6) примет вид (1.7.8):

(1.7.8)

но так как является корнем уравнения, то и, следовательно (1.7.9),

(1.7.9)

Для того чтобы итерационный процесс был сходящимся, необходимо выполнить условие (1.7.10)

(1.7.10)

или

(1.7.11)

Переход от уравнения (1.1.1) к уравнению (1.7.4) можно осуществить разными способами в зависимости от вида функции . При таком переходе необходимо построить функцию так, чтобы выполнялось условие сходимости (1.7.10). Рассмотрим один из общих алгоритмов перехода от уравнения (1.1.1) к уравнению (1.7.4).

Умножим левую и правую части уравнения (1.1.1) на произвольную константу и добавим к обеим частям неизвестное . При этом корни исходного уравнения не изменятся (1.7.11):

(1.7.11)

Введем обозначение (1.7.12)

(1.7.12)

и перейдем от соотношения (1.7.11) к уравнению (1.7.4).

Произвольный выбор константы позволит обеспечить выполнение условия сходимости (1.7.10). Желательно выбрать величину такой, чтобы , тогда сходимость итерационного процесса будет двухсторонней. В этом случае в наиболее простом виде можно представить критерий окончания итерационного процесса (1.7.13)