
- •Лекционно-практические занятия по теме
- •Понятие вектора. Виды векторов
- •Сложение и вычитание векторов
- •Умножение вектора на число векторов
- •Линейная независимость системы векторов. Понятие базиса
- •Базисом векторного пространства называется совокупность
- •Проекция вектора на ось
- •Свойства проекций:
- •Направляющие косинусы вектора
- •Действия над векторами в координатной форм
- •Координаты вектора, заданного начальной и конечной точками
- •Расстояние между двумя точками
- •Скалярное произведение векторов
- •Свойства скалярного произведения
- •Скалярное произведение в координатной форме
- •Векторное произведение векторов
- •Векторные произведения векторов декартового базиса
- •Векторное произведение в координатной фор
- •Применение векторного произведения
- •Смешанное произведение трех векторов
- •Свойства смешанного произведения
- •Смешанное произведение в координатной форм

Направляющие косинусы вектора
Z
a


Y
X
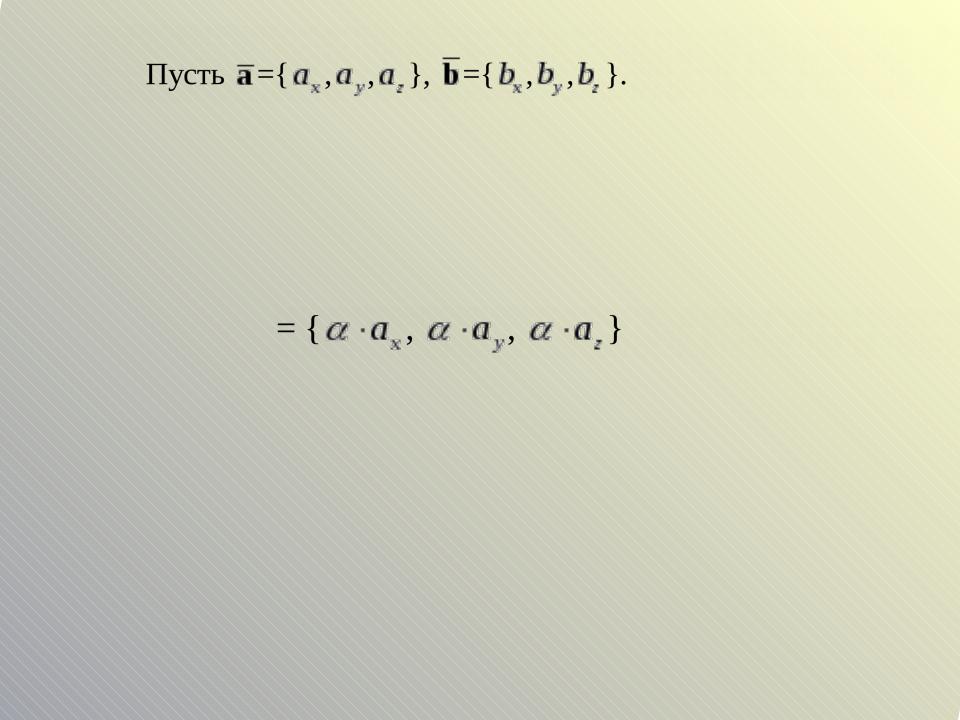
Действия над векторами в координатной форм
1. |
Сложение |
|
|
векторовa b ax bx ; ay by ; az bz |
|||
|
|
|
|
2. |
Вычитание векторов |
|
|
|
|
bx ; ay by ; az |
bz |
|
a b ax |
||
3. Умножение вектора на число
ba
4.Линейная комбинация векторов
a b ax bx ; ay by ; az bz
Условие коллинеарности векторов в координатной форме
Если два вектора коллинеарны, то
b a |
тогда |
bx |
|
||
|
|
by |
|
|
|
|
|
bz |
ax |
ax |
|
ay |
az |
|
|
откуда bx |
|
|
bz |
|
ay |
by |
||||
az |
|
|
|
|
|
Координаты коллинеарных векторов пропорциональны.
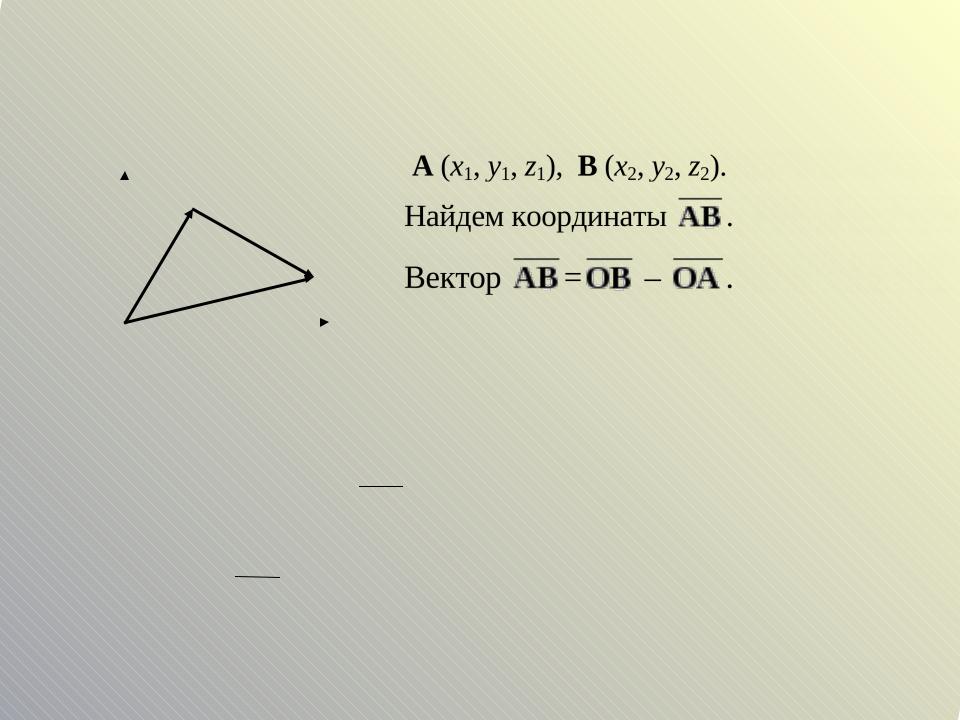
Координаты вектора, заданного начальной и конечной точками
Пусть известны координаты начала и конца вектора
Y |
|
A |
|
|
|
|
|||
|
|
|
||
|
|
|
B |
|
|
|
|
|
Векторы, выходящие из начала коорди |
O |
|
|
X |
|
|
|
в какую-либо точку, называются |
||
|
||||
|
|
|
|
радиус-векторами этой точки. |
Координаты радиуса-вектора точки совпадают с координатами самой точки, поэтому
OB ={x2, y2, z2}, OA ={x1, y1, z1},
И тогда AB ={x2 – x1, y2 – y1, z2 – z1}.
Координаты вектора равны разности соответствующих коорди конечной и начальной точек.
Расстояние между двумя точками
Если требуется найти расстояние |
между точкамиA(x ; y ; z ) и |
||||||||||||
B(x2 ; y2 ; z2 ) , то можно образовать вектор |
|
1 |
1 |
1 |
|||||||||
|
|
|
|
|
|||||||||
AB x2 x1; y2 y1; z2 z1 |
и найти его длину по известной |
||||||||||||
формуле |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
d |
AB |
|
(x |
2 |
x )2 ( y |
2 |
y )2 |
(z |
2 |
z )2 |
|
|
|
|
|
|
|
1 |
1 |
|
1 |
|
|
|
|||
Пример. Найти расстояние между точкамиA(5; 3;1) и B(3;6; 2) Решение. Образуем вектор, соединяющий точки, и найдем ег
AB 3 5;6 ( 3); 1 2 2;9; 3
d AB 
 ( 2)2 92 ( 3)2
( 2)2 92 ( 3)2 
 4 81 9
4 81 9 
 94
94

Скалярное произведение векторов
b
 a
a
ПРa b
Пример. Найти скалярное произведение векторов, если изв
Решение. |
|
a |
|
3 , |
|
b |
|
4 |
, 120o |
|
|
|||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
b) |
|
|
|
|
b |
|
cos |
3 4 cos120 |
o |
12 ( 0,5) 6 |
|||||||
|
|
|
|
|||||||||||||||
|
|
|
||||||||||||||||
(a |
|
a |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
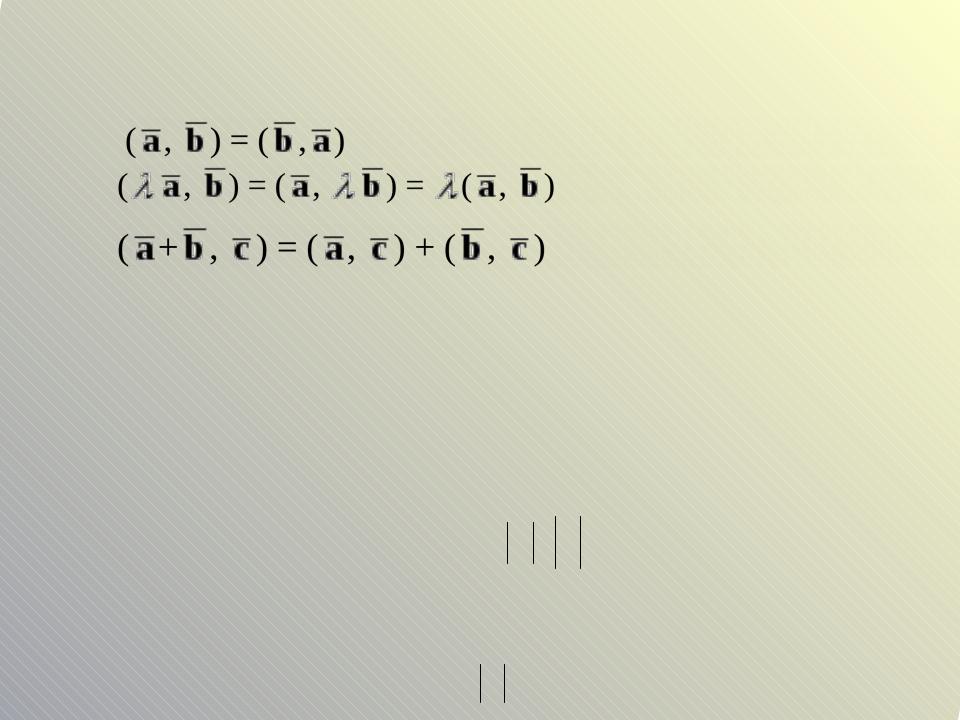
Свойства скалярного произведения
1.
2.
3.
4. Если два вектора перпендикулярны, тоaестьb , то
скалярное произведение равно их
нулю
5. Если два вектора коллинеарны, то их скалярное произведе равно произведению длин векторов. При этом произведени положительно, если векторы сонаправлены, и отрицательн направления противоположные
(a b) a b
В частности, скалярное произведение вектора самого на себя р скалярному квадрату вектора и равняется квадрату его длины
a a a 2 a 2
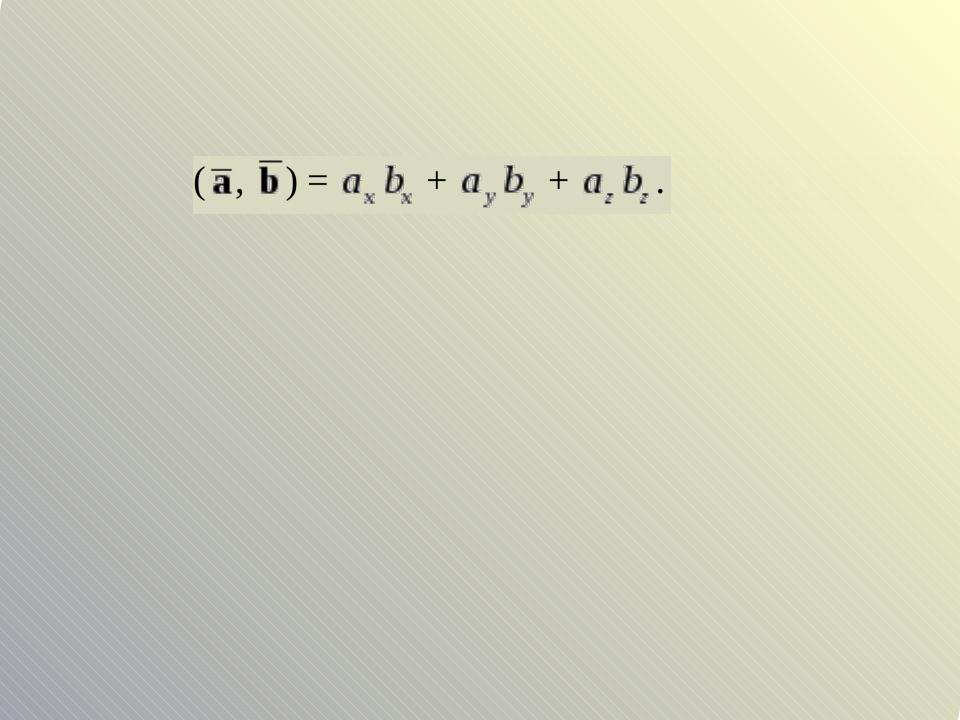
Скалярное произведение в координатной форме
Скалярное произведение в координатной форме равно сумм произведений соответствующих координат
Пример. Найти скалярное произведение векторов
a 2; 7;5 и |
b |
3;0; 4 |
Решение |
|
|
|
|
4) 6 0 20 26 |
(a b) 2 ( 3) ( 7) 0 5 ( |
||
Применение скалярного произведения
Скалярное произведение применяется для нахождения:
1.Длины вектора
2.Проекции вектора на вектор
3.Косинуса угла между векторами
4.Проверки условия перпендикулярности векторов
5.Работы силы по перемещению точки
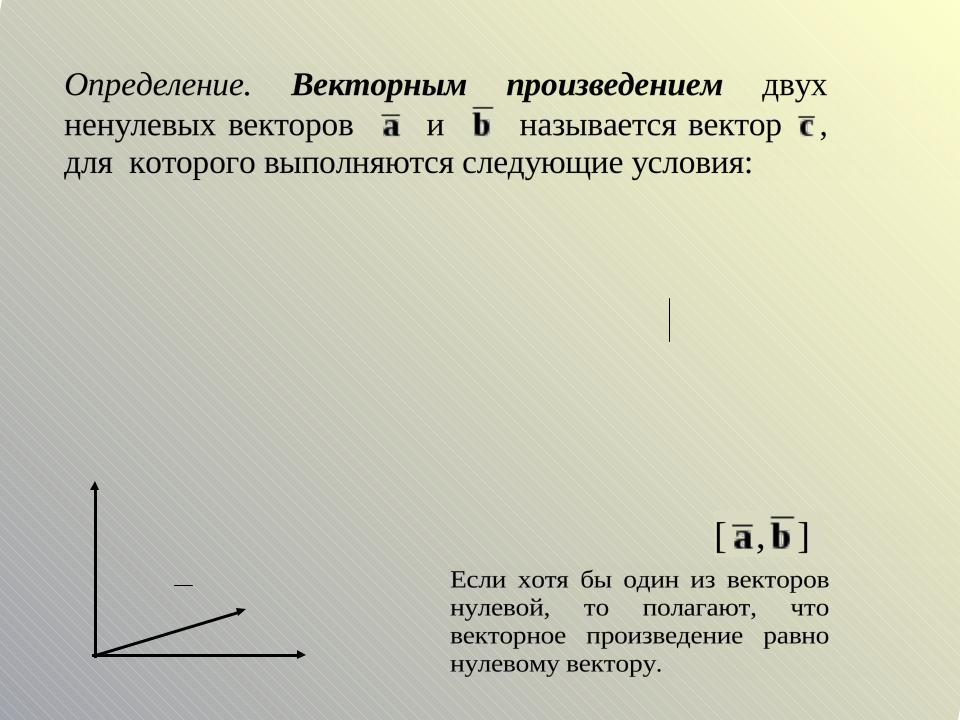
Векторное произведение векторов
1. Векторc перпендикулярен векторуa и векторуb ,
т.е. перпендикулярен плоскости, в которой лежат эти векторы
2. Длина вектораc |
равна произведению длин векторов |
|||||||||
на синус угла между векторами |
|
b | |
|
|
|
|||||
|
|
|
|
|
|
|
|
b |
sin |
|
|
|
|
c |
|
| a |
a |
||||
|
|
|||||||||
3. Векторc направлен так, что из его конца кратчайший |
||||||||||
|
a |
|
b |
|
виден против часовой стре |
|||||
поворот от вектора |
к вектору |
|||||||||
c a b |
Обозначения векторного |
|||||||||
произведения |
||||||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||||
|
|
c a b или |
||||||||
b

a
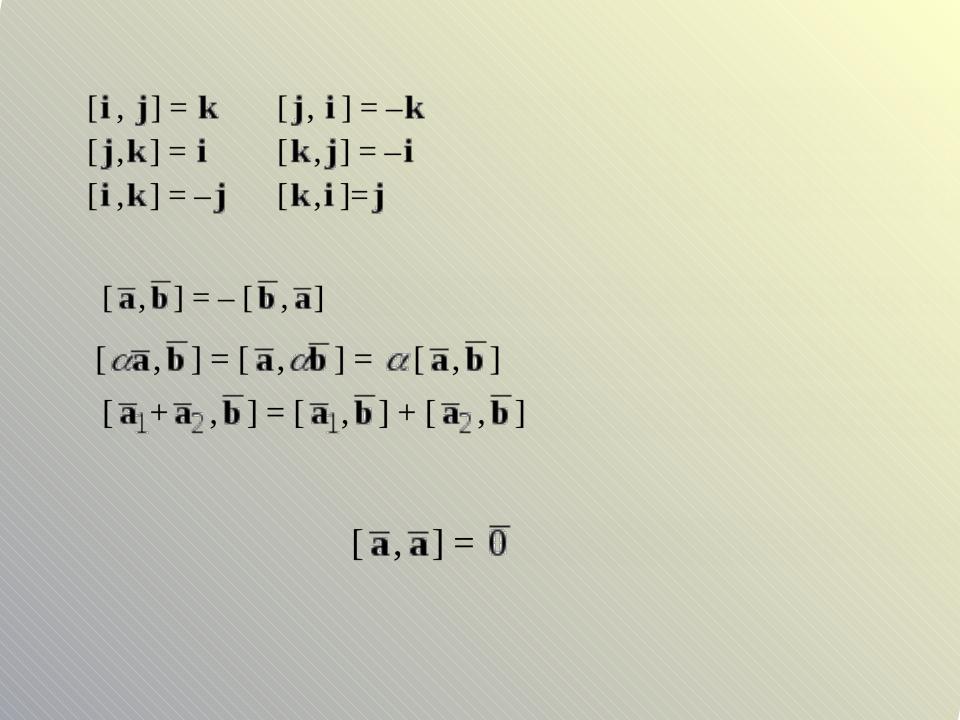
Векторные произведения векторов декартового базиса
Свойства векторного произведения
1.
2.
3.
4. Векторное произведение двух коллинеарных векторов равн В частности, если векторным образом перемножать вектор на себя, получится

Векторное произведение в координатной фор
Векторное произведение в координатной форме представляет с определитель третьего порядка, в первой строке которого стоя базисные векторы декартовой системы координат, а во второй и третьей строках – координаты перемножаемых ве
|
|
|
|
|
|
|
|
a 2; 7;5 |
|
|
|
Пример. Найти векторное произведение векторов |
|
|
|||||||
|
|
|
|
|
|
|
Решение. Составляем определительии |
|
||
|
b |
3;0; 4 |
|
|
||||||
|
i |
j |
k |
|
|
|
раскладываем его по элементам первой |
|
||
|
|
|
|
|||||||
|
2 |
7 |
5 |
|
|
|
строки |
|
|
|
|
|
|
|
|
|
|
||||
|
3 |
0 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
( 4) 5 |
||||||||
i ( 7) |
0 j |
(2 ( 4) 5 ( 3)) k (2 0 |
( 7) ( 3)) 28 i |
7 j 21 |
k |
|||||
