Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Политехнический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математика / practic2.ppt

Скачиваний:

Добавлен:

30.05.2015

Размер:

491.01 Кб

Скачать

☆

1 / 31 2 3 > Следующая >>>

Лекционно-практические занятия по теме

Векторная алгебра

Понятие вектора. Виды векторов

Вектором или

называется

направленный

начаaло и B

конец).

по-другому свободным вектором

отрезок (т.е. отрезок, у которого есть
Расстояние от начала вектора до его
конца называется длиной или модулем
AB	a	.
вектора и обозначается	или

Вектор, длина которого равна единице, называется единичным

вектором или ортом.

Вектор, начало и конец которого совпадают, называется нулев и обозначается0 . Нулевой вектор не имеет определенного направления и имеет длину, равную нулю.

Два вектораa		иb	называются ортогональными, если угол ме
ними равен 90.b				коллинеарными
Два вектораa			называются		, если они лежат
	и

на одной или параллельных прямых.

Три вектора, лежащие в одной или в параллельных плоскостях, называются компланарными.

Два вектора называются равными, если они имеют одинаковую длину и направление.

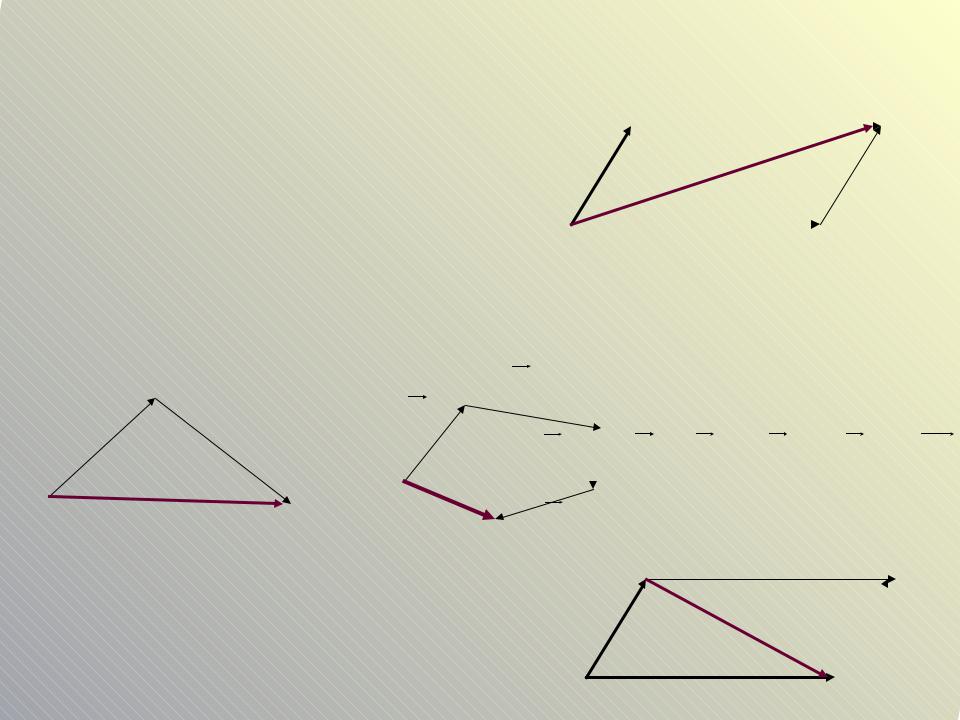
Сложение и вычитание векторов

Сложение векторов
Сложение векторов
(правило параллелограмма)				b	c a b
				b

Сложение векторов					a
Сложение векторов			Сложение векторов
(правило треугольника)			(правило многоугольника)
a	b	a1		a 2
				a 3	a a1 a 2 a 3 a4


				a 4
c	a b			a 4

Вычитание векторов

c a b

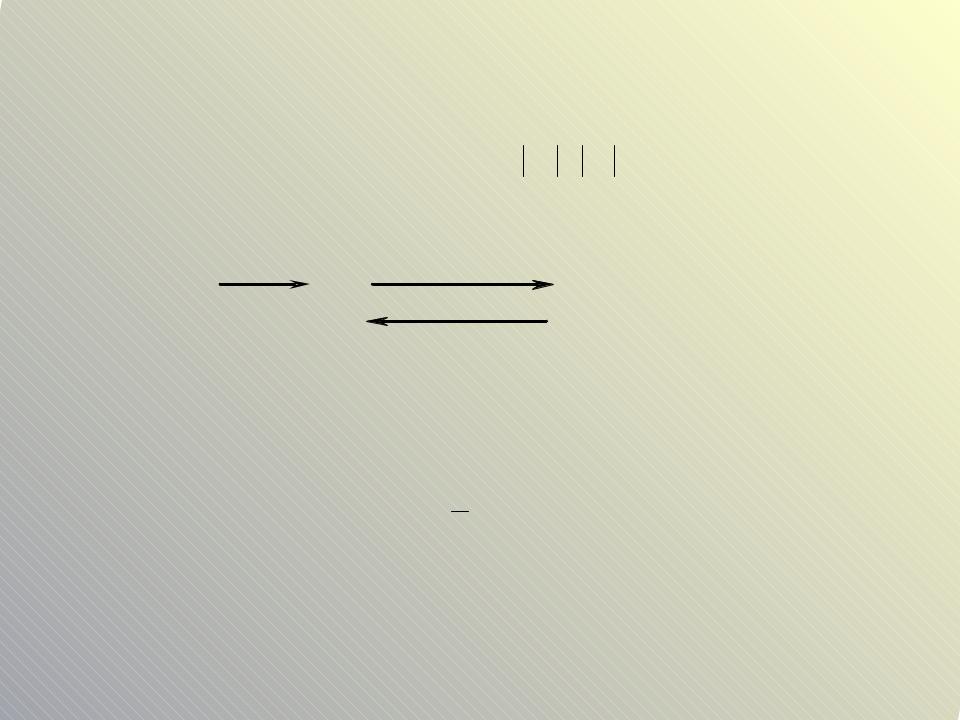
Умножение вектора на число векторов

Произведением вектора a на число 0

называется вектор, длина которого a , а направление совпадает с направлением вектора a при 0 и

противоположно ему при 0 .

При умножении вектора на (-1) получается противоположный ве

a = ( 1) a

Если два ненулевых вектора коллинеарны то один из них можн

выразить через другой

a b

Линейная независимость системы векторов. Понятие базиса

Совокупность векторов называется линейно зависимой, если линейная комбинация этих векторов равна нулю, причем не все

коэффициенты линейной комбинации равны нулю одновременно.

a 1 a1 2 a 2 3 a 3 ... n an 0

Совокупность векторов называется линейно независимой, если линейная комбинация этих векторов не равна нулю, причем равенство

	нулю возможно только в том случае, если все коэффициенты линейной
	комбинации равны нулю одновременно.	.
	a 1 a1 2 a 2 3 a 3 ... n an 0	.
	a 1 a1 2 a 2 3 a 3 ... n an 0
	Если векторы линейно зависимы, то,один из них можно представить
	в виде линейной комбинации остальных.

Три ненулевых вектора линейно зависимы тогда и только тогда,

когда они компланарны. В этом случае третий вектор

c a b

является линейной комбинацией двух других . Два ненулевых вектора линейно зависимы тогда и только тогда,

когда они коллинеарнaы b

Базисом векторного пространства называется совокупность

линейно независимых векторов, количество которых
определяется
размерностью пространства. Любой небазисный вектор является
линейной комбинацией базисных.			a
В одномерном пространстве -		один базисный вектор ,
остальные	b a			.
Все такие векторы будут лежать на одной прямой с векторомa
векторы можно записать в виде			.
Таким образом, одномерное пространство – это пространство

коллинеарных векторов.

В двумерном пространстве на плоскости будет два базисных вектора a и b , а любой третий вектор равен их линейной комбинации

Такой вектор является диагональю параллелограмма, построенного
на векторах a	и b	. Т.е. все три вектора будут компланарны.
на векторах a	и b
		c	a b
В трехмерном пространстве – три базисных вектора, а любой четверт
можно представить в видеd a b c
Выражения	b a ,
Выражения	b a ,		c a b ,	d a b c