
контролирующие материалы
Образцы входного контроля
Входной контроль по математике
Вариант 1
Вычислить в обыкновенных дробях

Вычислить

Представить в виде степени с основанием
 ,
,

Упростить и вычислить при

 ,
, .
.Упростить

Построить графики функций а)
 ,
б)
,
б) ,
в)
,
в)
Вычислить

Решить уравнения а)
 ,
б)
,
б) ,
в)
,
в) ,
г)
,
г)
Решить неравенства а)
 б)
б)
Найти область определения функций а)

Вычислить

Упростить

Найти общее решение уравнения

Входной контроль по математике
Вариант 2
Вычислить в обыкновенных дробях

Вычислить

Представить в виде степени с основанием
 ,
,

Упростить и вычислить при

 ,
, .
.Упростить

Построить графики функций а)
 ,
б)
,
б) ,
в)
,
в) .
.Вычислить

Решить уравнения а)
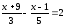 ,
б)
,
б) ,
в)
,
в) ,
,Решить неравенства а)
 б)
б)
Найти область определения функций а)

Вычислить

Упростить

Найти общее решение уравнения

Входной контроль по математике
Вариант 3
Вычислить в обыкновенных дробях

Вычислить

Представить в виде степени с основанием
 ,
,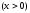

Упростить и вычислить при

 ,
, .
.Упростить

Построить графики функций а)
 ,
б)
,
б) ,
в)
,
в) .
.Вычислить

Решить уравнения а)
 ,
б)
,
б) ,
в)
,
в) ,
,Решить неравенства а)
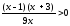 ,
б)
,
б) .
.Найти область определения функций а)
 , б)
, б)
Вычислить

Упростить


Найти общее решение уравнения
 .
.
Образцы текущего контроля
Вариант 1
1.
Дана система линейных уравнений 
найдите общее решение системы;
2.
Найдите длину вектора
 ,
если известно, что
,
если известно, что ,
,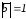 ,
, .
.
3. Плоскость проходит через точку M(6, −1, 1) и отсекает на оси Ox отрезок a = −3, на оси Oz отрезок c = 1. Составьте уравнение этой плоскости.
4. Приведите уравнение кривой к каноническому виду и постройте кривую
 .
.
5.
Постройте поверхность, определяемую
уравнением
 .
.
Вариант 2
1.
Дана система однородных линейных
уравнений 
найдите фундаментальную систему решений.
2.
Даны три вектора
 ,
, ,
,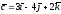 .
Найдите
.
Найдите .
.
3.
Составьте уравнение плоскости, которая
проходит через начало координат
перпендикулярно двум плоскостям
 :x – 2y + z −1 = 0
и
:x – 2y + z −1 = 0
и
 :x + y +3 z = 0.
:x + y +3 z = 0.
4.
Постройте кривую
 .
.
5.
Постройте поверхность, определяемую
уравнением
 .
.
Образцы рубежного контроля
ВАРИАНТЫ ЗАДАНИЙ
Контрольная работа по теме «Линейная алгебра»
1.
Дан определитель  .
.
а) Запишите разложение данного определителя по четвёртому столбцу;
б) вычислите определитель, получив предварительно нули в какой – либо строке или столбце.
2.
Решить систему уравнений
 матричным методом. Значение
матричным методом. Значение вычислить также методом Крамера.
вычислить также методом Крамера.
3. Исследовать систему на совместность и решить методом Гаусса

4.
Дана система однородных линейных
уравнений 
а) Докажите, что система имеет нетривиальные решения;
б) Найдите общее решение системы;
в) найдите фундаментальную систему решений.
При каких значениях параметра
 система линейных уравнений
система линейных уравнений
с
расширенной матрицей
 совместна?
совместна?
