
- •Лекционно-практическое занятие по теме
- •Раздел «Аналитическая геометрия ав пространстве» курса «Высшая математика» включает две основные темы:
- •Уравнения плоскости 4. Уравнение плоскости, проходящей через три
- •Построение плоскостей
- •Построение плоскостей
- •Таким образом, если в уравнении плоскости отсутствует одна переменная, то плоскость проходит параллельно
- •Взаимное расположение плоскостей
- •Расстояние от точки до плоскости
- •2. Прямая в пространстве. Основные
- •Прямая в пространстве. Основные
- •Взаимное расположение прямых в пространстве
- •Расстояние от точки до прямой в пространстве
- •Взаимное расположение прямой и плоскости в пространстве
- •Взаимное расположение прямой и плоскости в пространстве
- •Нахождение точки пересечения прямой и
- •Составление уравнений плоскости
- •Решение типовых задач контрольной работы № 4
- •Аналогично решаются задачи с такими условиями:
- •3. Составить уравнение плоскости, проходящей через две
- •4. Составить уравнение плоскости, проходящей черезM (2; 1;5)
- •5.Составить уравнение плоскости, проходящей через три
- •6. Составить уравнение плоскости, проходящей через
- •7. Составить уравнение плоскости, проходящей черезM (4; 2; 1)
- •8. Составить уравнение прямой, проходящей через точку
- •10. Составить уравнение прямой, проходящей черезM точку( 3; 1;5)
- •12. Составить уравнение прямой, проходящей черезMточку( 3;5; 2)
- •13. Перейти от общего уравнения прямой к каноническому
- •14. Составить уравнение прямой, проходящей через точку
- •15. Найти точку пересечения и угол между прямой
- •Угол между прямой и плоскостью находим по формуле
- •17. Найти расстояние от точки
- •3. Поверхности 2-го порядка
- •1. Сфера
- •Построение сферы
- •Построение сферы
- •Эллипсоид
- •Построить поверхностьx2 16 y2 4z2 8z 5
- •Гиперболоиды
- •Разные ориентации однополостных гиперболоидов
- •Гиперболоиды
- •Разные ориентации двуполостного гиперболоида
- •Конусы 2-го порядка
- •Конусы с разными осями симметрии
- •Параболоиды
- •Различные ориентации эллиптических параболоидов
- •Для построения эллиптического параболоида нужно знать:
- •Построить поверхность3z 1 2x2 5 y2
- •Гиперболический параболоид
- •Цилиндрические поверхности
- •Виды цилиндров
- •Эллиптические цилиндры
- •Гиперболические цилиндры
- •Построить поверхности
- •Построить поверхности

Лекционно-практическое занятие по теме
Аналитическая геометрия в пространстве

Раздел «Аналитическая геометрия ав пространстве» курса «Высшая математика» включает две основные темы:
1.Плоскость
2.Прямая в пространстве
3.Поверхности 2-го порядка
|
|
|
1. Плоскость |
|
|
|
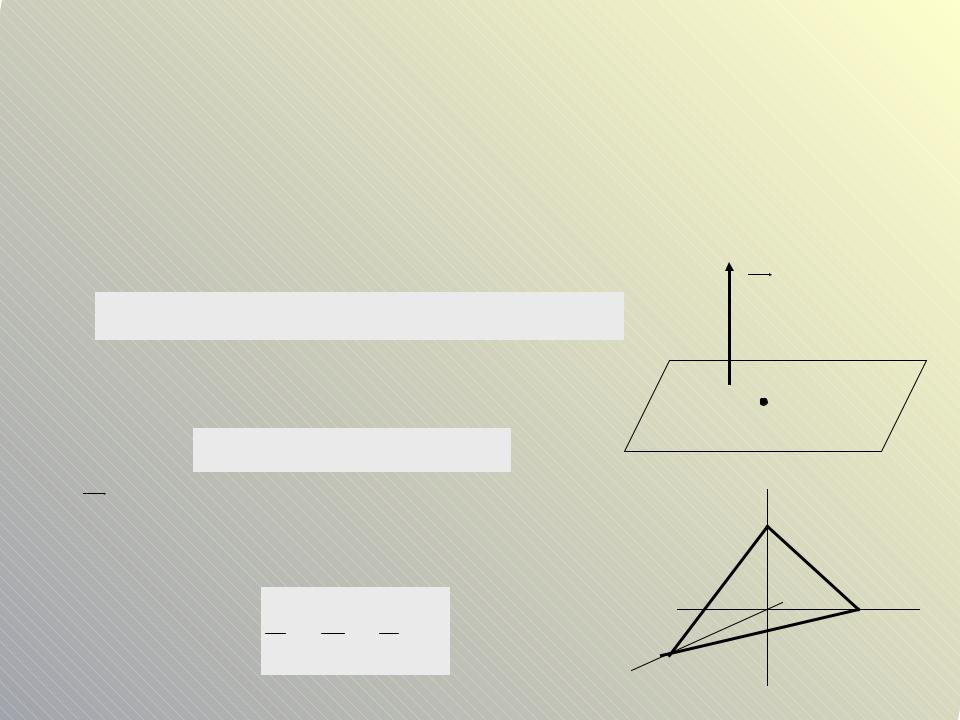
Основные уравнения плоскости |
|
|
||||
1. Уравнение плоскости, проходящей через |
|
|||||
|
M (x ; y ; z ) |
|
|
|||
заданную0 0 точку0 0 |
|
|
||||
перпендикулярно |
|
|
||||
|
|
|
|
N A; B;C |
N A; B;C |
|
A(x x0 ) B( y y0 ) C(z z0 ) 0 |
|
|||||
|
|
|||||
2. Общее |
|
|
плоскости |
M0 (x0 ; y0 ; z0 ) |
|
|
|
Ax By Cz D 0 |
|
|
|||
N A; B;C |
|
- вектор нормали |
Z |
|
||
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
3. Уравнение плоскости « в отрезках» |
|
|||||
|
|
x |
y |
z 1 |
b |
Y |
|
|
|
||||
|
|
a |
b |
c |
a |
|
|
|
|
|
X |
|
|
Уравнения плоскости 4. Уравнение плоскости, проходящей через три
|
|
M |
(x ; y ; z ) |
|
M |
2 (x2 ; y2 ; z2 ) |
|
M3 (x3 ; y3 ; z3 ) |
|||
заданные точки 1 |
1 1 1 |
|
, |
|
|
|
и |
||||
N A; B;C |
M (x; y; z) |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
M1M x x1; y y1; z z1 |
|||||
|
|
|
M2 (x2 |
; y2 |
; z2 ) |
||||||
M1 (x1; y1; z1 ) |
M1M2 x2 |
|
x1; y2 y1; z2 z1 |
||||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||
M3 (x3 ; y3 ; z3 ) |
M1M3 x3 x1; y3 y1; z3 z1 |
|
Условие компланарности векторов(M1M M1M 2 M1M3 ) 0
x x1 |
y y1 |
z z1 |
|
0 |
|
||||
x2 x1 |
y2 y1 |
z2 z1 |
|
|
x3 x1 |
y3 y1 |
z3 z1 |
|
|

Построение плоскостей
1. Построить плоскость3x 4 y 6z 12 0
Находим координаты точек пересечения плоскости с осями коо
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
||
x |
0 |
0 |
4 |
|
|
2 |
|
|
|
|
|
|
|
||||
y |
0 |
3 |
0 |
|
|
|
|
Y |
z |
2 |
0 |
0 |
4 |
|
|
3 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
||||
Можно привести уравнение плоскости к уравнению «в отрезках
|
|
|
3x 4 y 6z 12 |
|
|||||
1) Переносим вправо свободный член уравнения |
3x |
4 y |
6z |
|
|||||
2) |
Делим на 12, чтобы получить единицу в правой части |
12 |
1 |
||||||
3) |
x |
y |
|
z |
12 |
12 |
|||
Убираем коэффициенты из числителей |
|
|
1 |
|
|
|
|
||
|
4 |
|
|
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|
|||
Числа, стоящие в знаменателях, являются длинами отрезков, к
плоскость отсекает на осях координат
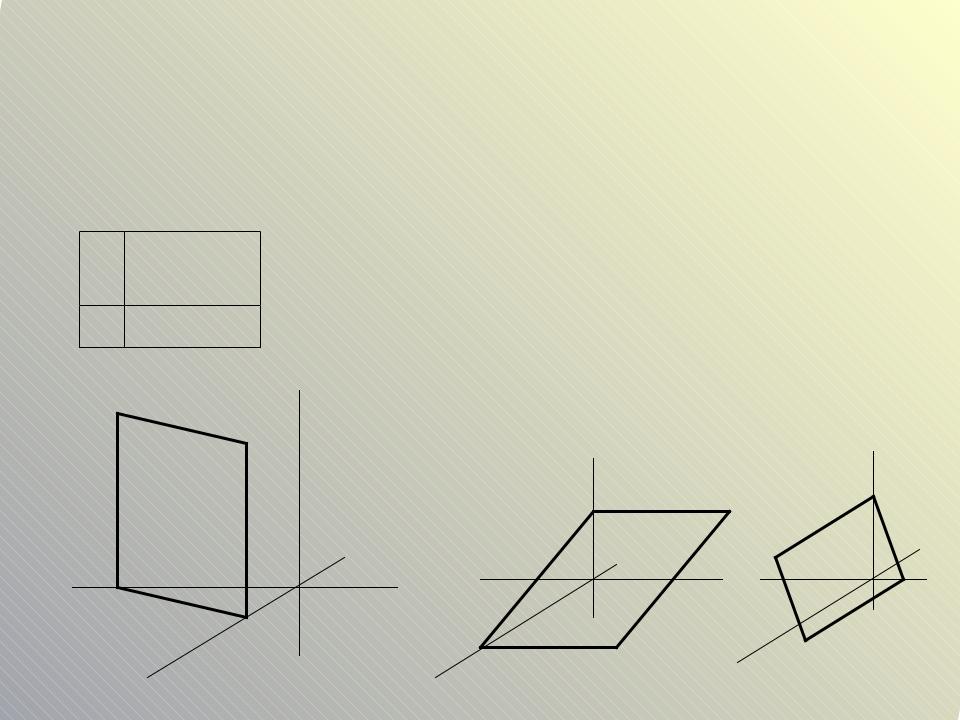
Построение плоскостей
2.Построить плоскость 3x 5y 10 0
Вуравнении отсутствует переменная z.
Находим точки пересечения плоскости с осями OX и OY.
X |
0 |
10/ |
Соединяем точки прямой линией и получаем |
|||||||
след плоскости на плоскости XOY. |
|
|||||||||
|
|
3 |
|
|||||||
|
|
Теперь из точек пересечения проводим |
||||||||
y |
-2 |
0 |
||||||||
прямые, параллельные оси OZ. |
|
|
||||||||
|
|
|
Z |
|
Аналогично строятся все плоскости, |
|||||
|
|
|
|
в уравнении которых отсутствует од |
||||||
|
|
|
|
|
переменнаяZ |
|
|
Z |
||
|
|
|
|
|
|
2 |
|
|
3 |
|
|
|
|
|
Y |
|
|
|
|
Y |
|
-2 |
|
|
|
|
7 |
Y |
|
2 |
||
|
10/3 |
|
|
|
|
|||||
|
|
|
|
X |
|
X |
|
|||
|
|
X |
|
|
2x 7z 14 0 |
|
3y 2z 6 |
|||
|
|
|
|
|
|
|||||
|
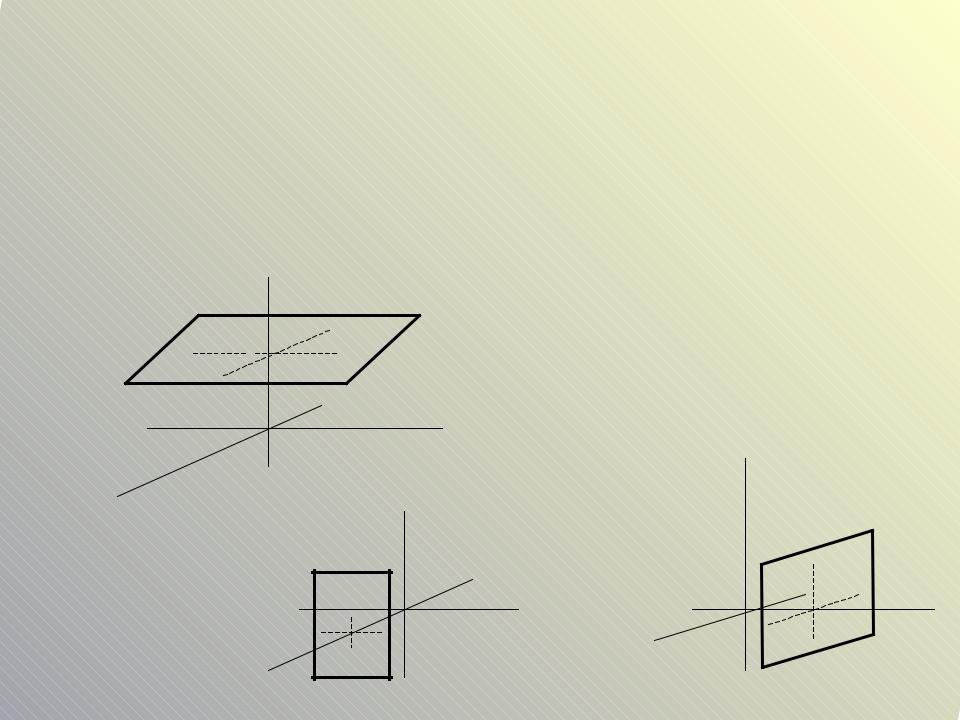
Построение плоскостей |
|
|
|||
3. Построить плоскость |
|
3z 8 0 |
|
|
||
В уравнении отсутствуют две переменные x и y. Такая |
||||||
плоскость |
|
|
|
|
|
|
проходит параллельно и оси OX , и оси OY, т.е. она проходит |
||||||
параллельно координатной плоскости XOY через точку z=8/3 |
||||||
на оси OZ. |
Z |
|
|
|
|
|
8/ |
|
|
Аналогично строятся плоскости, |
|||
|
|
|
||||
|
|
|
в уравнениях которых отсутствую |
|||
|
3 |
|
|
|||
|
|
|
две переменные |
|
|
|
|
|
|
Y |
|
|
|
|
0 |
|
|
|
|
|
X |
|
|
|
Z |
5 y 3 0 |
|
|
|
|
|
|||
|
4x |
9 0 |
Z |
|
|
|
|
|
|
|
Y |
|
Y |
|
X |
9/4 |
0 |
X |
0 |
3/5 |
|
|
|||||

Таким образом, если в уравнении плоскости отсутствует одна переменная, то плоскость проходит параллельно той оси координат, переменной которой нет в уравнении.
Если в уравнении плоскости отсутствует свободный член, то плоскость проходит через начало координат.
Если в уравнении плоскости отсутствуют две переменные, то плоскость проходит параллельно
координатной плоскости, переменных которой нет в уравнении.
Уравнения координатных плоскостей |
|
x 0 |
- уравнение плоскости YOZ |
y 0 |
- уравнение плоскости XOZ |
z 0 |
- уравнение плоскости |
|
XOY |
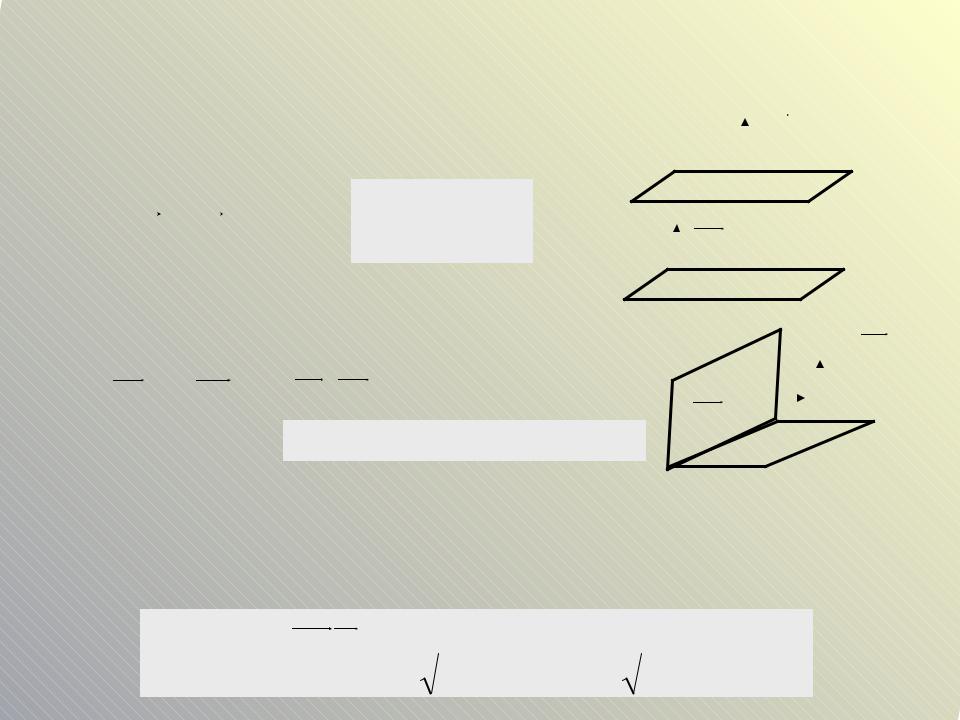
Взаимное расположение плоскостей
. |
Условие параллельности плоскостей |
|
N1 |
A1; B1;C1 |
||||||||||||
1 |
|
|||||||||||||||
|
N1 |
|| N2 |
A1 |
|
B1 |
C1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
A |
|
B |
2 |
C |
2 |
|
N |
A ; B |
;C |
2 |
|
||||
|
|
|
||||||||||||||
|
|
|
2 |
|
|
|
|
|
2 |
|
2 2 |
|
||||
2. Условие перпендикулярности плоскостей |
|
|
|
|
N1 |
||||
N1 |
|
|
N2 |
(N1 N2 ) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
N2 |
|
|
|||||||
|
|
|
|
||||||
|
|
|
|
A1 A2 B1 B2 C1 C2 0 |
|
|
|||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
3. Косинус угла между плоскостями
Угол между плоскостями – это угол между векторами нормалей этих плоскостей
cos cos(N1 |
,N 2 ) |
|
A1 A2 B1 B2 C1 C2 |
|
||||||
|
|
|
|
|
|
|
|
|
||
A2 |
B2 |
C 2 |
|
A2 |
B2 |
C 2 |
|
|||
|
|
|
|
|||||||
|
|
|
1 |
1 |
1 |
|
2 |
2 |
2 |
|
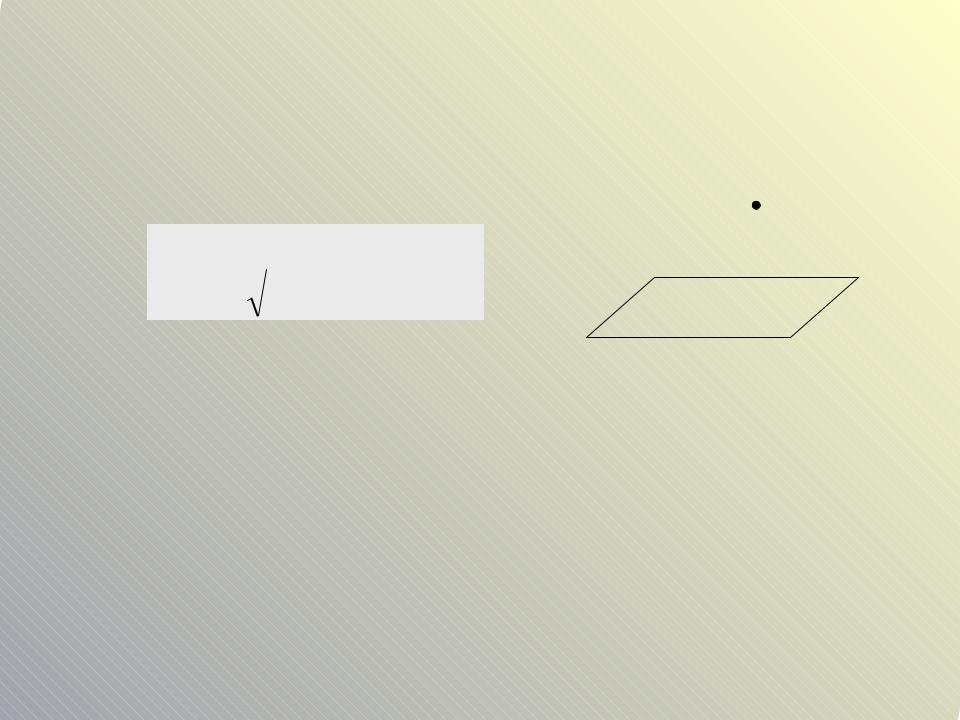
Расстояние от точки до плоскости |
|
|
||||||||
Расстояние от точки1 |
1 |
1 |
1 |
до плоскости |
|
|
||||
|
M |
(x |
; y |
; z ) |
|
|
|
|
|
|
Ax By Cz D 0 |
|
находится по формуле |
|
|
||||||
| Ax1 By1 Cz1 D | |
|
d |
|
M1 (x1 |
; y1 |
; z1 ) |
||||
|
|
|||||||||
|
|
|
|
|
||||||
d |
|
|
|
|
|
|
|
|
|
|
A2 B2 C 2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
Расстояние – это длина перпендикуляра, опущенного из точки на пло
Правило: для нахождения расстояния от точки до плоскости ну координаты точки подставить в левую часть уравнения плоскос разделить на длину вектора нормали плоскости и полученное з
взять по абсолютной величине.
!Расстояние – величина всегда положительная
