- •Дифференциальные уравнения
- •§16. Понятие устойчивости решения ДУ
- •2. Устойчивость по Ляпунову
- •ОПРЕДЕЛЕНИЕ. Решение
- •Геометрический смысл определения
- •ПРИМЕР1.Ислеоватьнаустойчивостьтривиальноере ниеy0уравненияy0.
- •ПРИМЕР2. Исследовать на устойчивость тривиальное реш- ние y 0уравнения y a2y (a const).
- •ПРИМЕР3. Исследовать на устойчивость тривиальное реш- ние y 0уравнения y a2y (a const).

Дифференциальные уравнения
Тема: Понятие устойчивости решения ДУ
Лектор Пахомова Е.Г.
2011 г.
§16. Понятие устойчивости решения ДУ
1. Предварительные замечания
ТЕОРЕМА 1 (о непрерывной зависимости решения от началь- ных условий).
Пусть для уравнения y = f(x,y) выполняются два условия:
1)f(x,y) непрерывна в некоторой области D плоскости xOy,
2)f y (x, y) в области D ограничена.
Тогда для любой точки M0(x0 ,y0) D решение y = (x) , удов- летворяющее начальному условию y0 = (x0) , непрерывно
зависит от начальных данных на отрезке [a;b], содер- жащем x0 .
Если решение задачи Коши , единственно и непрерывно зависит от начальных данных, то говорят, что задача Коши поставлена корректно.
2. Устойчивость по Ляпунову
Расмотримд.у. yf(x,y), (
где 1) f (x, y ) определена и непрерывна в некоторой области D (x; y) | x (a; ), y D1
2)f(x,y)ограиченавD |
||||
y |
|
|
|
|
Пусть |
|
|
|
|
1) y (x) – решение (1), |
|
удовлетворяющее начальному |
||
условиюy(x ) y (где y D, x (a; )); |
||||
0 |
0 |
0 |
1 |
0 |
~ |
|
уовлетворяющеначальном |
||
2) y y(x)–решение(1), |
||||
|
~ |
|
|
|
условиюy(x) y. |
|
|
|
|
0 |
0 |
|
|
|
Преполагается,чторешения(x)и~y(x)опреленыд
всехxx(говорят:«неограниченопролжаемывправо
0

ОПРЕДЕЛЕНИЕ. Решение |
y = (x) |
уравнения |
y = f(x,y) |
|||||||
называ- |
|
|
|
|
|
при x + , |
|
|||
ется |
устойчивым по Ляпунову |
если для |
||||||||
любого > 0 существует |
> 0 такое, что для всякого ре- |
|||||||||
шения |
y = y(x) |
|
~ |
|
|
|
|
~ |
|
|
|
|
|
|
|
||||||
|
этого уравнения |
|
|
|
из неравенства |
|
||||
|
|
|
y(x0 ) (x0 ) |
|
|
y0 |
y0 |
|
||
~
(2)
следует неравенство y(x) (x)
(3)
для всех x x0.
(т.е. решения, близкие по начальным значениям к решению y = (x) , остаются близкими и при всех x x0).
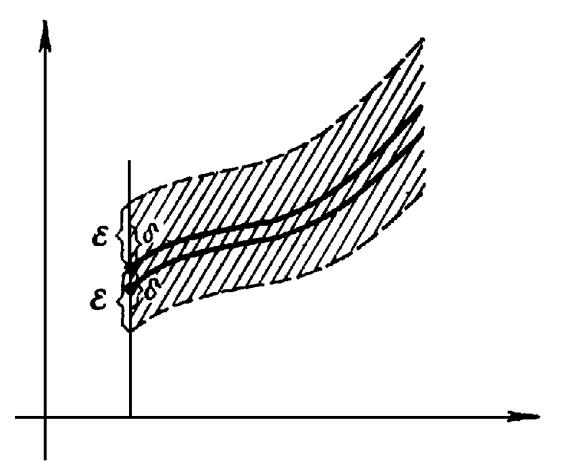
Геометрический смысл определения
y
x0
y (x)
~
y y(x)
x
Решение y = (x) устойчиво, |
если для любой -полоски, |
содержащей кривую y = (x) , |
достаточно близкие к ней при |
x = x0 интегральные |
кривые y = y(x) целиком содержатся в |
указанной -полоске |
при всех x x0 . |
Если при сколь угодно малом > 0 хотя бы для одного решения y = y(x) уравнения (1) неравенство (3) не выполняется, то решение y = (x) этого уравнения называется неустойчивым.
Неустойчивым следует считать и решение, не продолжаемое вправо при x + .

ОПРЕДЕЛЕНИЕ. Решение y = (x) уравнения (1) называется
асимптотически устойчивым, если
1) решение y = (x) устойчиво,
2) существует 1 > 0 такое, что для любого решения
y = y(x) уравнения (1), удовлетворяющего условию
~
y(x0 ) (x0 ) 1 ,
|
lim |
|
~ |
(x) (x) |
|
0. |
|
|
|
|
|
||||
имеем |
|
y |
|
(4) |
|||
x |
|
|
|
|
|
||
|
|
|
|
|
|
|
(т.е. все решения y = y(x) , близкие по начальным условиям к асимптотически устойчивому решению y = (x), не только остаются близкими к нему при x x0, но и неограниченно
сближаются с ним при x + ).
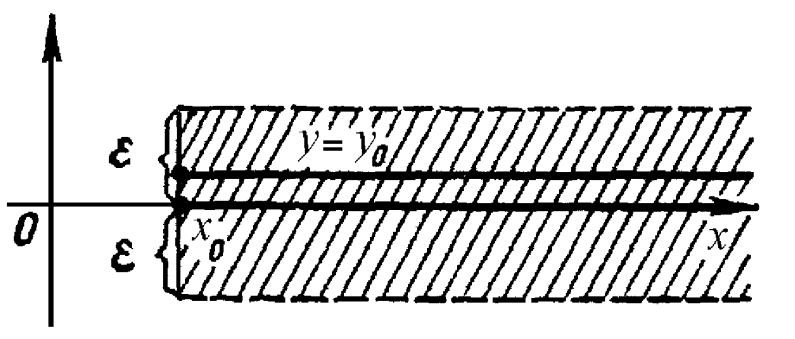
ПРИМЕР1.Ислеоватьнаустойчивостьтривиальноере ниеy0уравненияy0.
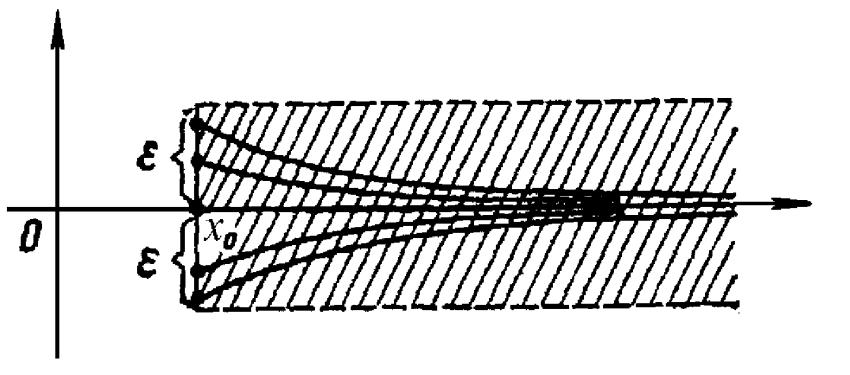
ПРИМЕР2. Исследовать на устойчивость тривиальное реш- ние y 0уравнения y a2y (a const).