
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:все лекции по самочерновой / 2 курс МОИ Лекции по ФУНКЦИЯМ КОМПЛЕКСНОЙ ПЕРТФКП САМОЧЕР.pptx
X
- •ТЕОРИЯ
- •КОМПЛЕКСНЫЕ
- •САМОЧЕРНОВ
- •Равенство двух комплексных чисел ОПРЕДЕЛЕНИЕ
- •2. Действия над
- •4. Тригонометрическая форма комплексного числа
- •Переход от алгебраической формы записи комплексного числа к тригонометрической
- •Пример
- •Действия над комплексными
- •Определение предела последовательности
- •ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ПРЕДЕЛА ПОСЛЕДОВАТЕЛЬНОСТИ К. Ч.
- •ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ПРЕДЕЛА ПОСЛЕДОВАТЕЛЬНОСТИ К. Ч.
- •СЛЕДСТВИЯ
- •СЛЕДСТВИЯ
- •ЗАМЕЧАНИЕ
- •ПРИМЕР
- •ЗАМЕЧАНИЕ
- •Предел и непрерывность функции
- •ЗАМЕЧАНИЕ
- •ОСНОВНЫЕ
- •ПОКАЗАТЕЛЬНАЯ
- •ЛОГАРИФМИЧЕСКАЯ
- •ТРИГОНОМЕТРИЧЕСКИЕ
- •ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
- •• ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
- •ОБРАТНЫЕ
- •Аналогично, как обратные к соответствующим операциям, вводятся операции
- •§4. Дифференцирование функции комплексной переменной
- •Дифференцирование функции комплексной переменной
- •Дифференцирование функции комплексной
- •дифференцируемости)
- •УСЛОВИЯ КОШИ- РИМАНА
- •Аналитическая функция
- •Гармонические функции
- •Геометрический смысл модуля и аргумента производной
- •Геометрический смысл модуля
- •Геометрический смысл
- •Геометрический смысл модуля и аргумента
- •Геометрический смысл модуля и аргумента производной
- •ПРИМЕР
- •ИНТЕГРИРОВАНИЕ
- •§ 5. Интегрирование функции комплексной переменной
- •Свойства интегралов от
- •Вычисление интегралов от ф.к.п.
- •Теорема 5.1. (теорема
- •Теорема 5.2. (теорема Коши для односвязной области)
- •Теорема 5.4. (теорема Коши для многосвязной области)
- •Теорема 5.5. (интегральная формула Коши)
- •Теорема 5.6.
- •Пусть на комплексной плоскости введена полярная

ТЕОРИЯ
ФУНКЦИЙ
КОМПЛЕКСНОГО
ПЕРЕМЕННОГО

КОМПЛЕКСНЫЕ
ЧИСЛА.
ПОСЛЕДОВАТЕЛЬНО СТИ КОМПЛЕКСНЫХ ЧИСЕЛ
САМОЧЕРНОВ
ОЙ
самочерновой


Равенство двух комплексных чисел ОПРЕДЕЛЕНИЕ
• |
Пусть |
|
|
|
|
|
z1 = x1 + iy1 , z2 = x2 + iy2 . |
||||
• |
z |
= z |
если |
||
|
1 |
x |
x |
2 |
|
|
21 |
|
|||
|
|
y |
y |
2 |
|
|
|
1 |
|
|
|

2. Действия над
комплексными числами в алгебраической форме


4. Тригонометрическая форма комплексного числа
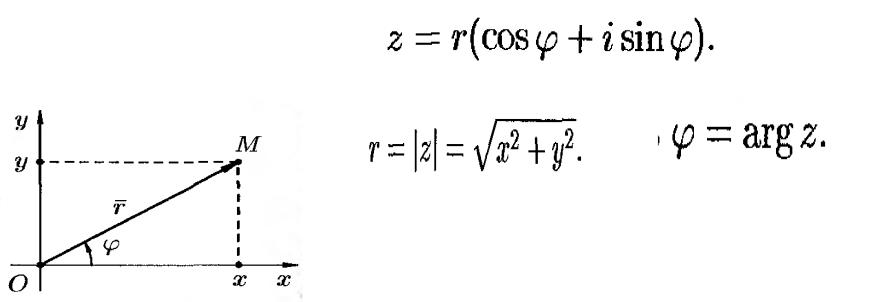
Переход от алгебраической формы записи комплексного числа к тригонометрической
• Z = x+ iy ,
•
|
1 ,x 0, y 0 |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 ,x 0, y 0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
, |
tg 1 |
|
|
|
|
. |
||||
|
|
|
|
|
||||||
|
|
|
||||||||
|
1 ,x 0, y 0 |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
2 1 ,x 0, y 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
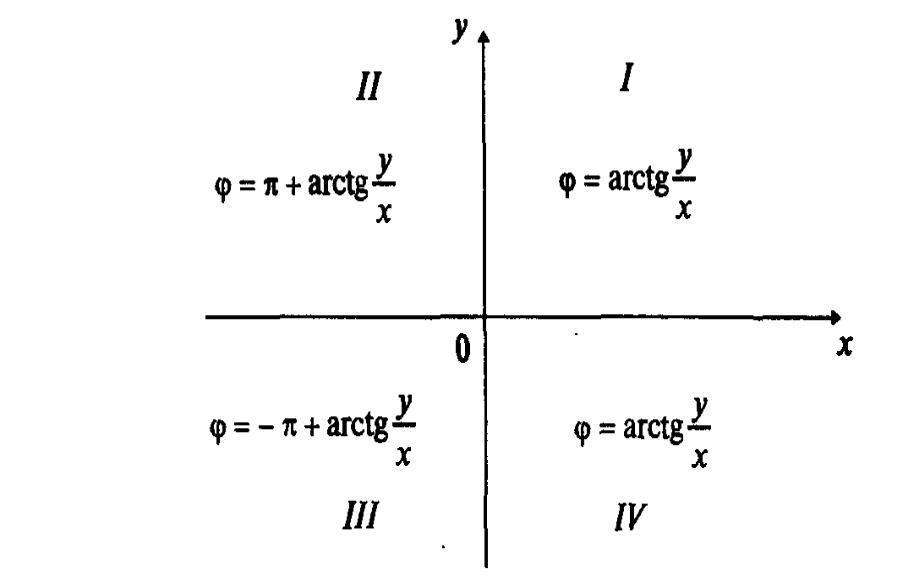
Соседние файлы в папке все лекции по самочерновой
