
все лекции по самочерновой / кабплоскость
.pdf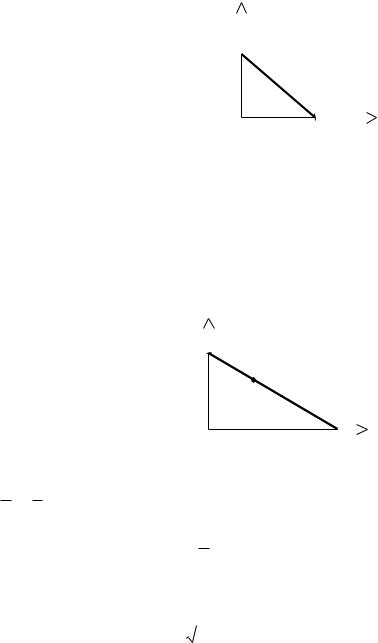
Задача 3. Дано уравнение плоскости 3x 3y 2x 6 0. Найти точки
пересечения этой плоскости с координатными осями.
Решение. Используя уравнение (3.9) перенесем свободный член в правую часть равенства с противоположным знаком и разделим обе части равенства на 6:
|
|
|
|
|
|
|
|
|
|
x |
|
|
y |
|
z |
1, |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
||||||
т.е. a 2, b 2, c 3 точки пересечения плоскости |
с |
координатными |
||||||||||||||||||||||||
осями - A1 (2,0,0) , |
|
A2 (0, 2,0) , |
A3 (0,0,3) . |
|
|
|
|
|
|
|
||||||||||||||||
Ответ: A1 (2,0,0) , |
A2 (0, 2,0) , |
A3 (0,0,3) . |
|
|
|
|
|
|
|
|||||||||||||||||
Задача 4. |
Вычислить площадь |
треугольника, отсекаемого прямой |
||||||||||||||||||||||||
3x 4y 12 0 от координатного угла (рис. 36). |
|
|
|
|
|
|
|
|||||||||||||||||||
Решение. Найдем отрезок a и b, отсекаемый |
У |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
прямой от координатных осей: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
3x |
4 y |
|
|
x |
|
y |
|
|
|
3 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
3x 4 y 12 |
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||
12 |
12 |
4 |
3 |
b |
|
|
|
|
||||||||||||||||||
a 4; b 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х |
|||
Найдем |
площадь |
|
заштрихованного |
О |
|
|
|
|||||||||||||||||||
|
a |
4 |
||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
прямоугольного треугольника (рис. 36) |
|
|
|
|
|
|
|
Рис. 36 |
|
|||||||||||||||||
S |
1 |
a b |
1 |
4 3 6 кв. ед. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: S = 6 кв. ед.
Задача 5. Составить общее уравнение прямой, которая проходит через точку С(1,1) и отсекает от координатного угла треугольник с площадью,
равной 2 кв. ед. в первой четверти (рис. 37). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. Будем искать уравнение |
У |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
прямой “в отрезках” |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x |
|
y |
1, причем a > 0 и b > 0. |
|
|
|
|
|
|
|
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
a |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Так как |
точка С(1,1) принадлежит этой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
прямой, то ее координаты (х =1, у = 1) будут |
О |
1 |
|
а |
|||||||||||||||
|
|
||||||||||||||||||
удовлетворять уравнению этой прямой |
|
|
|
|
|
|
|
|
|
Рис. 37 |
|
|
|
|
|||||
1a b1 1 b a a b .
Площадь заштрихованного треугольника S 12 a b 2 . Тогда получим два уравнения относительно неизвестных a и b:
a b 4 |
|
a b 4 a 4 b (4 b) b 4 |
|
|||
|
|
|
|
|
|
b = 2, |
|
|
|
|
|
||
a b a b |
|
b 2 |
4b 4 0 b 2 |
4 4 2 |
|
|

тогда a b4 42 2 и уравнение прямой “в отрезках” имеет вид
2x 2y 1 x y 2. Тогда общее уравнение прямой x y 2 0.
Ответ: x y 2 0.
Проведем исследование уравнения прямой, когда в нем отсутствуют некоторые члены. Результаты исследования и геометрическая иллюстрация приведены в табл. 1.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1 |
||||||||
|
|
|
Вид уравнения |
|
Геометрическая |
|
|
|
|
Вид уравнения |
Геометрическая |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
иллюстрация |
|
|
|
|
|
|
|
|
|
|
|
|
иллюстрация |
|
|
|
|
|
|||||||||||||||||
|
Ax By C 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ax C 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
x |
|
|
y |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
1, |
x a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
a |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
A 0, B 0, C 0 |
|
|
|
|
|
|
|
|
|
|
|
Х |
|
|
A 0, B 0, C 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Х |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
О |
|
а |
|
|
|
|
|
О |
|
|
|
|
а |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
прямая || оси ОУ |
|
|
|||||||||||||
|
By C 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ax By 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
b |
1, y b |
|
|
|
|
|
|
|
|
|
|
|
|
|
a b 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
A 0, B 0, C 0 |
|
|
|
|
|
|
|
|
|
|
|
Х |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
О |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ay bx, y a x |
|
|
|
|
|
|
О |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
прямая оси ОХ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
A 0, B 0, C 0 |
прямая проходит |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
через начало |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
координат |
|
|
|
|
|
|||||||||||
|
Ax 0 |
|
|
У |
|
|
|
|
|
|
|
|
By 0 |
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
x 0 |
|
|
|
|
|
|
|
х=0 |
|
|
y 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
A 0, B 0, C 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
A 0, B 0, C 0 |
|
|
|
|
|
|
|
|
у=0 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х |
|
||
|
|
|
|
|
|
|
|
|
О |
ось ОУ |
|
|
|
|
|
|
|
|
|
|
|
О |
|
ось ОХ |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Выводы:
1.Если в уравнении прямой присутствуют все члены, то прямая пересекает координатные оси и отсекает от них отрезки а и b.
2.Если в уравнении прямой отсутствует свободный член, то прямая проходит через начало координат.
3.Если в уравнении прямой отсутствует член, содержащий х или у, то прямая проходит параллельно оси отсутствующей координаты.
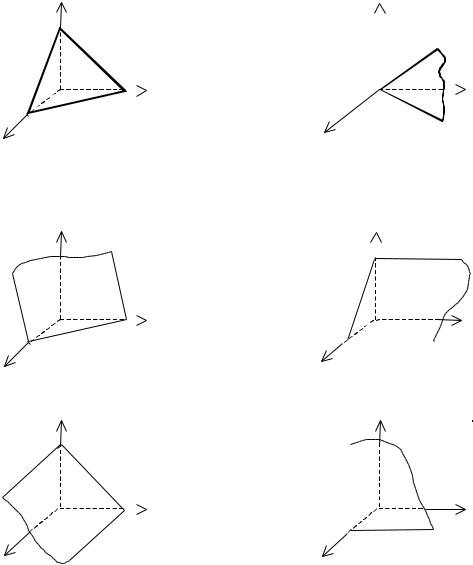
Исследование общего уравнения плоскости
Общее уравнение плоскости может быть полным или неполным, т.е. в нем могут отсутствовать одно или несколько слагаемых. Вид уравнения определяет ориентацию плоскости в пространстве. Для построения плоскости лучше использовать уравнение “в отрезках”. Исследование общего уравнения плоскости представлено в табл. 2.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2 |
||||||
Вид уравнения |
Геометрическая |
Вид уравнения |
Геометрическая |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
иллюстрация |
|
|
|
|
|
|
|
|
иллюстрация |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|||
Ax By Cz D 0 |
с |
|
|
|
|
|
|
|
Ax By Cz 0 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
x |
|
|
y |
|
|
|
z |
1 |
|
|
|
|
|
|
|
|
|
|
|
A 0, B 0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
C 0, D 0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
a |
b |
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
плоскость |
|
|
|
|
|
|
|
|
|
|
|
|
|
плоскость |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пересекает оси |
|
|
|
|
|
|
|
проходит через |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
OX, OY, OZ |
|
|
|
|
|
|
|
|
|
|
|
|
|
начало координат |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Ax By D 0 |
Z |
|
|
|
|
|
|
|
|
Ax Cz D 0 |
|
|
|
с |
|
Z |
|
|
|
||||||||||||||||||||||||
|
|
|
x |
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
c |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
a |
b |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
A 0, B 0 |
а |
|
|
|
|
|
A 0, B 0 |
а |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
C 0, D 0 |
|
|
|
|
|
У |
C 0, D 0 |
|
|
|
|
|
|
У |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
плоскость |
|
оси |
|
|
|
|
|
|
|
плоскость оси |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
OZ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
OУ |
|
|
|
|
|
|
|
||||||
By Cz D 0 |
с |
Z |
|
|
|
|
|
|
Ax D 0 |
|
|
|
|
|
|
Z |
|
|
|
|
|||||||||||||||||||||||
|
|
|
y |
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
b |
c |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
A 0, B ,0 |
|
|
|
|
|
|
|
|
A 0, B 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
C 0, D 0 |
|
|
|
|
|
|
|
|
У |
C 0, D 0 |
|
a |
|
|
|
|
|
У |
||||||||||||||||||||||||
|
Х |
|
|
|
|
|
|
Х |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
плоскость |
|
оси |
|
|
|
|
|
|
|
плоскость |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
OХ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
плоскости ZOY |
|
|
|
||||||||||
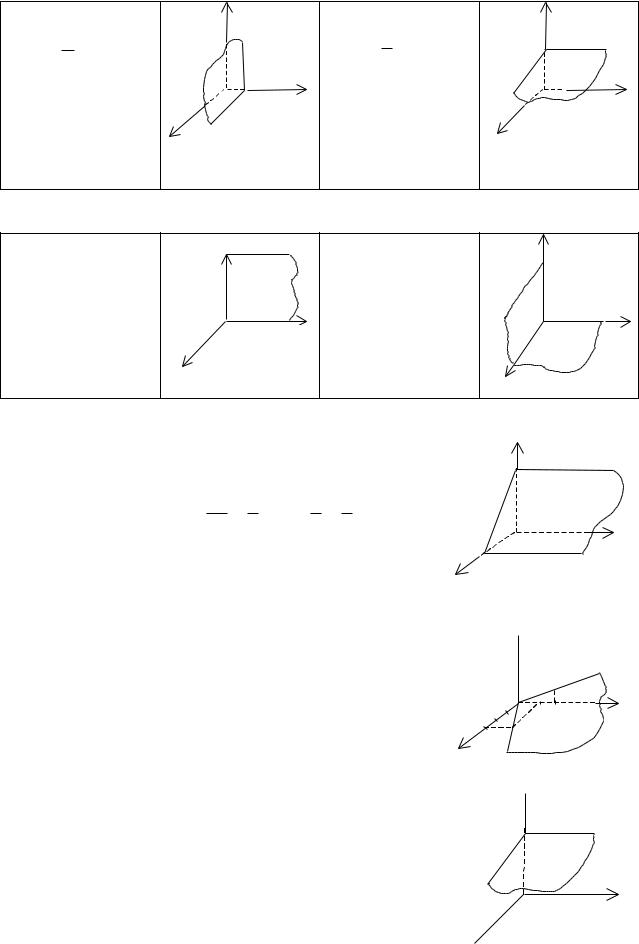
By D 0 |
Z |
|
|
|
Cz D 0 |
|
|
Z |
y |
|
|
|
|
z |
|
|
с |
b 1 |
|
|
|
|
c 1 |
|
|
|
A 0, B 0 |
|
|
|
|
A 0, B 0 |
|
|
|
C 0, D 0 |
|
b |
У |
|
C 0, D 0 |
|
|
У |
|
|
|
|
|
|
|
||
Х |
|
|
|
|
|
|
Х |
|
плоскость |
|
|
|
плоскость |
||||
плоскости XOZ |
|
|
|
плоскости XOУ |
||||
|
|
|
|
|
|
|
Окончание табл. 2 |
|
Ax 0 |
|
|
|
|
By 0 |
|
|
Z |
A 0, B 0 |
Z |
|
|
|
A 0, B 0 |
|
у=0 |
|
C 0, D 0 |
|
|
|
|
C 0, D 0 |
|
|
|
|
|
|
|
|
Cz 0 |
|
|
0 |
|
|
0 |
У |
|
|
|
|
|
|
|
|
A 0, B 0 |
|
|
У |
||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
Х |
|
|
|
|
C 0, D 0 |
|
Х |
|
плоскость ZOY |
|
|
|
|
|
|||
Задача 6. Построить следующие плоскости: |
|
|
|
|||||
1) 4x z 8 0; 2) 6x 2y z 0; 3) z 5 0 . |
|
8 |
Z |
|||||
|
|
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
1) 4x z 8 0 |
4x |
z |
1 x |
z |
1, |
|
|
|
|
8 |
8 |
4 |
8 |
|
4 |
|
|
т.е. a 4, c 8 (рис. 38). |
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
||
Плоскость 4x z 8 0 параллельна оси ОУ; |
Х |
|
|
|
Рис. 38 |
2) плоскость 6x 2y z 0 проходит через начало координат, т. к.
свободный член D 0. Найдем уравнение прямой, по которой данная плоскость пересекается с
плоскостью ХОУ (рис. 39):
z 0 6x 2y 0 y 3x ;
Найдем уравнение прямой, по которой данная
плоскость пересекается с плоскостью YOZ: x 0 2y z 0 z 2y .
3) z 5 0 z 5. Данная плоскость параллельна плоскости XOY (рис. 40).
Выводы:
1.Если в уравнении плоскости отсутствует свободный член, то плоскость проходит через начало координат.
2.Если в уравнении плоскости отсутствует одна координата, то плоскость параллельна оси
Z 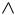 z=2y
z=2y
2
1 



3 |
У |
Х
Рис. 39
Z 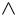
5
0 У
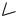 Х
Х
отсутствующей координаты. |
Рис. 40 |
3.Если в уравнении плоскости отсутствуют две координаты, то плоскость параллельна координатной плоскости отсутствующей координаты.
4.Если в уравнении плоскости отсутствуют две координаты и свободный член, то это есть координатная плоскость отсутствующих координат.
3.2. Каноническое и параметрическое уравнения прямой на плоскости и в пространстве
Пусть дана фиксированная точка M 0 и вектор l . Выведем уравнения
прямой на плоскости и в пространстве, проходящие через эту точку ( M 0 )
параллельно вектору l .
Определение 1. Вектор, параллельный данной прямой или лежащий на этой прямой, называется направляющим вектором прямой.
|
|
|
|
|
Будем выводить эти уравнения одновременно на плоскости и в |
||||||||||||||||||||||||||||||||||||
пространстве. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
На плоскости: |
|
|
|
|
|
|
|
|
|
|
|
|
В пространстве: |
|||||||||||||||||||||
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
М0(х0,у0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М0(х0,у0,z0) |
|
l (m, n, p) |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
l (m, n) |
|
|
|
|
|
|
|
|
|
r0 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
r0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М(х,у) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М(х,у,z) |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х |
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
О |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
О |
|
|
|
|
|
|
|
|
|
|
Х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
Рис. 41 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 42 |
||||||||||
M 0 (x0 , y0 ) – фиксированная точка; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
M 0 (x0 , y0 , z0 ) – фиксированная точка; |
||||||||||||||||||||||||||||||||||||||||
М(х,у) |
– текущая |
|
точка |
с |
|
||||||||||||||||||||||||||||||||||||
|
|
М(х,у,z) – текущая точка с переменными |
|||||||||||||||||||||||||||||||||||||||
переменными координатами; |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
координатами; |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
l |
(m, n) |
|
– направляющий вектор |
|
|
|
|
|
– |
направляющий вектор |
|||||||||||||||||||||||||||||||
прямой. |
|
|
|
|
|
|
|
|
|
|
|
|
l (m, n, p) |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
прямой. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Из условия коллинеарности векторов M 0 M |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
и l |
следует |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
M 0 M tl , но M 0 M r r0 ; |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
r |
r0 t |
l , где t - некоторый параметр. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Выразим радиус-вектор текущей точки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
r0 |
|
t l |
|
. |
|
|
|
|
|
|
|
(3.11) |
|||||||||||||

Уравнение (3.11) называется параметрическим уравнением прямой на плоскости и в пространстве. Запишем это уравнение в координатной форме:
|
прямая в пространстве: |
|
|
|
|
|
|
прямая на плоскости: |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
x x0 tm |
|
|
|
|
|
|
|
|
|
|
|
x x0 |
tm |
. |
(3.13) |
|||||||||
|
|
|
|
y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
y |
tn |
, |
|
|
(3.12) |
|
|
|
|
|
|
y y0 |
tn |
|
|
|||||||||
|
|
|
|
z0 |
tp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Если из уравнений (3.12) и (3.13) исключить параметр t, то получим |
||||||||||||||||||||||||||
уравнение прямой, которое называется каноническим |
|
|
|
|
|
|
|||||||||||||||||||||
|
M 0 M (x x0 , y y0 , z z0 ) , |
|
|
|
M 0 M (x x0 , y y0 ) , |
|
|||||||||||||||||||||
|
x x0 |
|
y y0 |
|
z z0 |
. |
(3.14) |
|
|
|
|
x x0 |
|
y y0 |
. |
|
(3.15) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
m |
|
n |
|
|
p |
|
|
|
|
|
|
m |
|
n |
|
|
|
|
||||||||
|
Из канонического уравнения можно получить уравнение прямой, |
||||||||||||||||||||||||||
проходящей через 2 фиксированные точки ( M 1 и M 2 ) (рис. 43): |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
M2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 43 |
|
|
|
|
|
|
||||||||
M1 (x1 , y1 ), M 2 (x2 , y2 ) – |
|
|
|
|
M1 (x1 , y1 , z1 ), M 2 (x2 , y2 , z2 ) – |
|
|||||||||||||||||||||
фиксированные точки; |
|
|
|
|
фиксированные точки; |
|
|
||||||||||||||||||||
M (x, y) – текущая точка с |
|
|
M (x, y, z) – текущая точка с |
||||||||||||||||||||||||
переменными координатами. |
|
|
|
|
переменными координатами. |
|
|||||||||||||||||||||
Вектор M1M 2 является направляющим вектором прямой.
M1M 2 (x2 x1 , y2 y1 ) ; |
M1M 2 (x2 x1 , y2 y1 , z2 z1 ) ; |
||||||||||||||
M1M (x x1 , y y1 ) ; |
M1M (x x1 , y y1 , z z1 ) ; |
||||||||||||||
M1M || M1M 2 , |
следовательно, их |
M1M || M1M 2 , следовательно, их |
|||||||||||||
координаты пропорциональны: |
координаты пропорциональны: |
||||||||||||||
|
|
x x1 |
|
y y1 |
|
. (3.16) |
|
|
x x1 |
|
y y1 |
|
z z1 |
|
. (3.17) |
|
|
x2 x1 |
y2 y1 |
|
|
|
y2 y1 |
z2 z1 |
|||||||
|
|
|
|
|
|
x2 x1 |
|
|
|||||||
Уравнения (3.16) и (3.17) называются уравнениями прямой, проходящей через две точки.
Выводы:
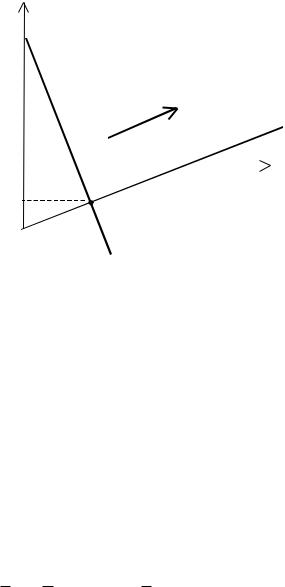
1. Для составления уравнения прямой на плоскости необходимо знать:
а) фиксированную точку M 0 (x0 , y0 ) и нормальный вектор прямой N ( A, B) , перпендикулярный данной прямой;
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(m, n) |
|||
|
б) фиксированную точку M 0 (x0 , y0 ) и направляющий вектор l |
|||||||||||||||||||||||||||||||||||||||||
, параллельный данной прямой; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
в) две фиксированные точки M1 (x1 , y1 ) и M 2 (x2 , y2 ) ; |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
г) |
фиксированную точку |
M 0 (x0 , y0 ) и тангенс угла наклона |
k tg , |
||||||||||||||||||||||||||||||||||||||
образованный прямой с осью ОХ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
с) значения отрезков, отсекаемых прямой от координатных осей. |
|||||||||||||||||||||||||||||||||||||||||
|
2. Для составления уравнения прямой в пространстве необходимо |
|||||||||||||||||||||||||||||||||||||||||
знать: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
а) |
фиксированную |
|
точку |
M 0 (x0 , y0 , z0 ) |
и направляющий |
вектор |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l (m, n, p) , параллельный данной прямой; |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
б) две фиксированных точки M1 (x1 , y1 , z1 ) и M 2 (x2 , y2 , z2 ) . |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
Задача 1. |
Составить уравнения |
прямых на плоскости, проходящих |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
через точку |
|
M 0 (2, 1) перпендикулярно вектору N |
и параллельно вектору N |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, если |
N (3,4) (рис. 44). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Решение. |
|
Найдем |
|
уравнение У |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
прямой |
l1 : |
вектор N l1 |
, т.е. |
N |
|
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
нормальный вектор прямой. Будем |
|
|
|
|
|
|
|
|
|
|
|
|
|
N (3,4) |
|
|
|
|
||||||||||||||||||||||||
использовать уравнение (3.2): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
A(x x0 ) B( y y0 ) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
3(x 2) 4( y 1) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
l1 |
: 3x 4y 2 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Найдем уравнение прямой l2 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
вектор N || l2 , т.е. N |
является |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M0(2,-1) |
|
|
|
|
||||||||||||||||||||
направляющим вектором прямой l2 . |
|
|
|
|
|
|
|
|
|
|
|
l1 |
|
|
|
|
|
|
||||||||||||||||||||||||
Будем использовать уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 44 |
|
|
|
|
||||||||||||||||||||
(3.14): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
x x0 |
|
y y0 |
|
x 2 |
|
y 1 |
|
4(x 2) 3( y 1) |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
m |
|
|
|
|
n |
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l2 : 4x 3y 11 0. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Ответ: l1 : 3x 4y 2 0; |
|
l2 : |
4x 3y 11 0 . |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
Задача 2. Составить уравнения прямой, |
проходящей через точки |
||||||||||||||||||||||||||||||||||||||||
M1 (3, 2) и |
|
|
|
|
M 2 ( 5,1) , вычислить угловой коэффициент k этой прямой. |
|||||||||||||||||||||||||||||||||||||
|
Решение. Будем использовать уравнение (3.16): |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
x x1 |
|
|
y y1 |
|
|
|
x 3 |
|
|
y 2 |
|
|
x 3 |
|
y 2 |
3x 8y 7 0. |
|||||||||||||||||||||||||
|
|
|
x |
|
|
|
5 3 |
1 2 |
|
|
||||||||||||||||||||||||||||||||
|
x |
2 |
|
|
y |
2 |
y |
|
|
|
|
|
|
|
|
8 |
3 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Выразим у в явном виде, т.е. приведем к уравнению с угловым коэффициентом ( y kx b) :
8y 3x 7 y 83 x 78 , т.е. k 83 .
Ответ: y |
3 |
x |
7 |
и k |
3 |
. |
||
8 |
8 |
8 |
||||||
|
|
|
|
|
||||
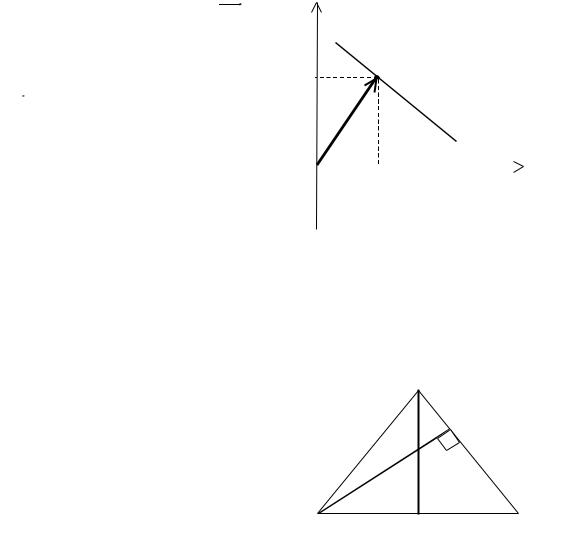
Задача 3. Составить |
уравнения прямой, если точка P(2,3) , |
|||||||
принадлежащая этой прямой, служит основанием перпендикуляра, опущенного из начала координат на эту прямую (рис. 45).
Решение. |
Вектор |
OP |
У |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
перпендикулярен |
прямой |
l, |
|
|
|
|
|
|
|
|
|
|
|
|
||
следовательно он является нормаль- |
|
|
|
|
|
|
Р(2,3) |
|||||||||
ным вектором прямой |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
OP (2 0,3 0) (2,3) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
l |
|
|
|
|
||||
Для нахождения уравнения прямой l |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
будем использовать |
уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Х |
|
|||||
(3.14) |
|
|
|
|
0 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
A(x x0 ) B( y y0 ) 0 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2(x 2) 3( y 3) 0 |
|
|
|
|
|
|
|
Рис. 45 |
||||||||
2x 3y 13 0. |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: |
l : |
2x 3y 13 0. |
|
|
|
|
|
|
|
|
|
|
|
|
||
Задача |
4. |
Даны |
вершины |
треугольника: |
|
A(1, 1), B( 2,1), C(3,5) . |
||||||||||
Составить уравнение высоты, проведенной из вершины А и медианы, проведенной из вершины В (рис. 46).
Решение. Найдем уравнение высоты AD. Для этого найдем уравнение стороны ВС как уравнение прямой, проходящей через точки В и С:
|
x xB |
|
|
y yB |
|
|
x 2 |
|
|
y 1 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
xC xB |
|
|
|
yC yB |
|
|
|
|
3 2 |
|
|
5 1 |
|
|
|||||||
|
x 2 |
|
|
y 1 |
. |
|
|
|
|
|
|
|
|
|
|
|
А(1,-1) |
E |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
5 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 46 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
BC : 4x |
5y 13 0 |
|
|
|
|
|
(4, 5) BC , следовательно, вектор |
|
||||||||||||||
|
|
и N |
N |
|||||||||||||||||||
направляющим вектором высоты AD. |
|
|
||||||||||||||||||||
|
|
|
|
|
|
AD : x x A |
y y A , где N (m, n) (4, 5) |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
n |
|
|
||||||
|
|
|
|
|
|
|
x 1 |
|
y 1 |
|
5x 4 y 1 0 5x 4 y 1 0. |
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
|
|
|
||||
уравнение
С(3,5)
является
Найдем уравнение медианы ВЕ. Медиана делит противоположную сторону пополам. Тогда найдем координаты точки Е из формул деления отрезка пополам:
x |
|
|
x A xC |
|
1 3 |
2; |
y |
|
|
y A yC |
1 5 2 E(2,2) . |
E |
|
|
E |
|
|||||||
|
2 |
2 |
|
|
2 |
2 |
|||||
|
|
|
|
|
|||||||

Составим уравнение медианы ВЕ как уравнение прямой, проходящей через точки В и Е:
|
BE : |
x xB |
|
y yB |
|
|
|
|
x 2 |
|
y 1 |
|
x 2 |
|
y 1 |
x 4 y 6 0. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
xE xB |
|
|
yE yB |
|
|
|
|
2 2 |
|
2 1 |
4 |
|
|
|
|
1 |
|
|
|||||||||||||||||||
|
Ответ: высота AD: 5x 4 y 1 0; медиана ВЕ: |
|
x 4y 6 0. |
||||||||||||||||||||||||||||||||||||
|
Задача 5. Составить каноническое и параметрическое уравнения |
||||||||||||||||||||||||||||||||||||||
прямой, |
проходящей |
|
|
через |
|
точку |
|
M1 (2,0, 3) |
|
|
|
параллельно вектору |
|||||||||||||||||||||||||||
|
(2, 3,5) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Решение. Каноническое и параметрическое уравнения прямой в |
||||||||||||||||||||||||||||||||||||||
пространстве имеют вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
x x |
|
|
|
|
|
y y |
|
|
|
z z |
|
|
|
|
|
|
x x0 |
mt, |
|||||||||||||||||
|
|
|
|
0 |
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
y y0 |
nt, |
||||||||||||||||
|
|
|
|
|
m |
|
|
|
|
|
n |
|
|
p |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z z0 |
pt, |
|||||||||
|
|
является направляющим вектором прямой; |
|||||||||||||||||||||||||||||||||||||
где a (m, n, p) |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x 2 |
|
|
|
|
y 0 |
|
|
z 3 |
|
|
|
|
|
x 2 2t, |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3t, |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
y |
|
|
|
|
|||||||||||||
|
|
|
2 |
|
|
|
|
3 |
|
5 |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
5t. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|||||||||||
|
Ответ: каноническое уравнение |
x 2 |
|
|
y 0 |
|
|
z 3 |
; |
||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
5 |
|
|
|||||
x 2 2t,
параметрическое уравнение y 3t,
z 3 5t.
Задача 6. Даны вершины треугольника: A(3,6, 7) , B( 5,2,3) и C(4, 7, 2) . Составить параметрическое уравнение его медианы,
проведенной из вершины С (рис. 47).
Решение. Медиана CD делит стороны АВ пополам, значит,
x |
|
|
x A xB |
|
3 5 |
1; |
y |
|
|
y A yB |
|
|
6 2 |
|
4; |
|||||||
D |
|
|
|
|
D |
|
|
|
||||||||||||||
|
|
|
|
2 |
|
2 |
|
|
|
2 |
|
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
z |
|
|
z A zB |
|
7 3 |
2; D( 1,4, 2) . |
|||||||||||||
|
|
|
D |
|
||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Найдем параметрическое уравнение DC с |
|
|
|
B |
|
|||||||||||||||||
направляющим вектором |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
DC (xC xD , yC yD , zC z D ) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
D |
|
|
|
|
|
|||||||||||||
(4 1, 7 4, 2 2) (5, 11,0) (m, n, p); |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
x xC mt 4 5t, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
nt |
7 11t, |
|
|
|
|
|
|
|
|
|
|
|
||||||
DC : y yC |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
pt |
2. |
|
|
|
|
|
A |
|
|
|
|
C |
||||||
z zC |
|
|
|
|
|
|
|
|
|
|
||||||||||||
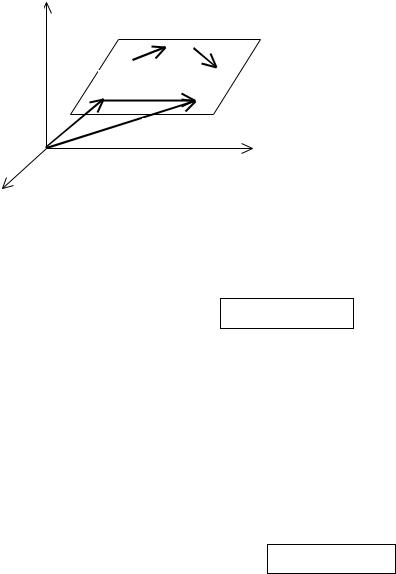
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.47 |
|
|
|
|
|
|
|
x 4 5t, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11t, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: DC : y 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.3. Параметрическое уравнение плоскости |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть |
дана |
фиксированная |
|
точка |
|
|
M 0 (r0 ) и |
два |
неколлинеарных |
|||||||||||||
|
|
|
|
уравнение |
плоскости, |
проходящей через |
точку |
||||||||||||||||
вектора a и b . Выведем |
|||||||||||||||||||||||
(M 0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
параллельно векторам a и b . Векторы |
a и b |
можно параллельным |
|||||||||||||||||||||
переносом опустить в искомую плоскость как свободные векторы (рис. 48). |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
M |
|
(x |
|
, y |
|
, z |
) - фиксированная точка, |
|||||||
Z |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
0 |
|
0 |
|
|
|
|
|
|
|
a |
|
|
|
a (a1 , a2 , a3 ) , |
|
b (b1 , b2 , b3 ) , |
|
(a || b) ; |
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
M (x, y, z) |
- текущая точка с переменными |
||||||||||||||||
|
M 0 |
|
М |
|
координатами. |
|
|
|
|
|
Вектор |
||||||||||||
r0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
r |
|
|
|
|
|
M 0M |
r r 0 (x x0 , y y0 , z z0 ) . |
||||||||||||||
|
|
|
У |
Векторы |
|
|
|
|
|
|
- |
лежат |
в |
одной |
|||||||||
0 |
|
|
|
|
a, b , |
|
r |
r |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
плоскости, т.е. являются компланарными, |
||||||||||||||||||
Х |
|
|
|
|
следовательно, |
|
они |
являются |
линейно |
||||||||||||||
|
Рис. 48 |
|
|
зависимыми и один из них является |
|||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
линейной комбинацией остальных, т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
r |
r0 |
pa |
qb . |
|
|
|
|
|
|
|
|
||||||||
Выразим радиус-вектор текущей точки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
r0 pa |
qb . |
|
|
|
|
|
|
|
|
|
|
|
(3.18) |
||||||
Получим параметрическое уравнение плоскости в векторном виде. Запишем |
|||||||||||||||||||||||
это уравнение в координатной форме: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
x x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
0 |
pa |
|
qb , |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.19) |
|||
|
|
|
|
y y0 |
pa2 |
qb2 , |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z z |
0 |
pa |
3 |
|
qb . |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|||
|
Воспользуемся условием компланарности трех векторов и выведем еще |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
два |
уравнения |
плоскости. |
Векторы |
|
|
r |
r0 , |
a, b - компланарны, |
|||||||||||||||
следовательно, их смешанное произведение равно нулю: |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 . |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
(r |
r0 , a, b) |
|
|
|
|
|
|
(3.20) |
|||||||||||
|
Запишем это уравнение в координатной форме: |
|
|
|
|
|
|||||||||||||||||
