ДУ в.п., допускающие понижение порядкаwww.themegallery.

Линейные ДУ высшего порядкаwww.themegallery.

com

Определение. Линейными дифференциальными уравнениями n-го

Если ai (x) = const, i = 1,…, n , то уравнение называется линейным ДУ n-го порядка с постоянными коэффициентами.

Если b (x) 0, то уравнение называется линейным однородным.

Если b (x) 0, то уравнение называется линейным неоднородным.

Линейные ДУ высшего порядкаwww.themegallery.

com

Свойства решений ЛОДУ в п.

то функция y = C y1 (x), где С = const, тоже является решением этого ДУ.

2. Если y1 , y2 – решения ЛОДУ в п (2), то функция (y1 + y2) – тоже является решением этого ДУ.

3. Если y1 , y2, …, y k – решения ЛОДУ в п (2), то функция

(С1 y1 + С2 y2 + Сk y k)

– тоже является решением этого ДУ для любых постоянных С1, С2, …, Сk.

ЛОДУ n-го порядка wwwcom .themegallery.

Пусть система из n функций y1, y2,…, yn – определена и непрерывна на интервале (a, b).

Определение. Функции y1, y2,…, yn называются линейно зависимыми на (a, b) если существует числа 1, 2,…, n R такие, что на этом интервале выполняется тождество

функции y1,y2,…, yn называются линейно независимыми на (a, b).

ЛОДУ n-го порядкаwwwcom .themegallery.

функции y1, y2,…, yn линейно зависимые и имеют производные до (n-1)-го порядка, то их определитель Вронского тождественно равен нулю.

Теорема 2. Если n решений y1, y2,…, yn ЛОДУ высшего порядка (2) линейно независимы на (a, b), то их определитель Вронского не может обращаться в ноль ни в одной точке интервала (a, b).

Следствие. Определитель Вронского системы функций y1, y2,…, yn , являющихся решениями ЛОДУ в п (2) либо тождественно равен нулю, если система решений линейно зависима, либо не обращаться в ноль ни в одной точке, если система решений линейно независима.

Структура общего решения ЛОДУwww.themegallery.

com

Определение. Система n линейно независимых решений ЛОДУ n – го порядка называется его фундаментальной системой.

Теорема 3. (О структуре общего решения ЛОДУ )

Если функции y1 (x), y2 (x),…, y n (x) , x (a, b) – образуют фундаментальную систему решений ЛОДУ (2) на интервале

(a,b), то ,

где ci – const, является общим решением этого уравнения.

Общее решение ДУ в пwww.themegallery. com

Определение. Функция y = (x, С1, С2,…,Сn) называется общим

решением ДУ

y(n)) = f (x, y, y', y'',…y (n-1)) ,

внекоторой области D существования и единственности решения задачи Коши если она удовлетворяет условиям:

1)при любом допустимом значении постоянных С1, С2,…,Сn оно удовлетворяет ДУ;

2) каковы бы ни были начальные условия

y0 = y (x0), y0' = y ' (x0), y0 ' ' = y ' ' (x0), …, y0(n-1) = y (n-1) (x0),

ЛОДУ с постоянными коэффициентамиwww.themegallery.

com

Определение. Линейными однородными дифференциальными уравнениями с постоянными коэффициентами называют уравнения вида

называется характеристическим уравнением ЛОДУ с постоянными коэффициентами, а многочлен

kn + p1 k n-1 + …+ pn-1 k + pn –

характеристическим многочленом.

www.themegallery. com

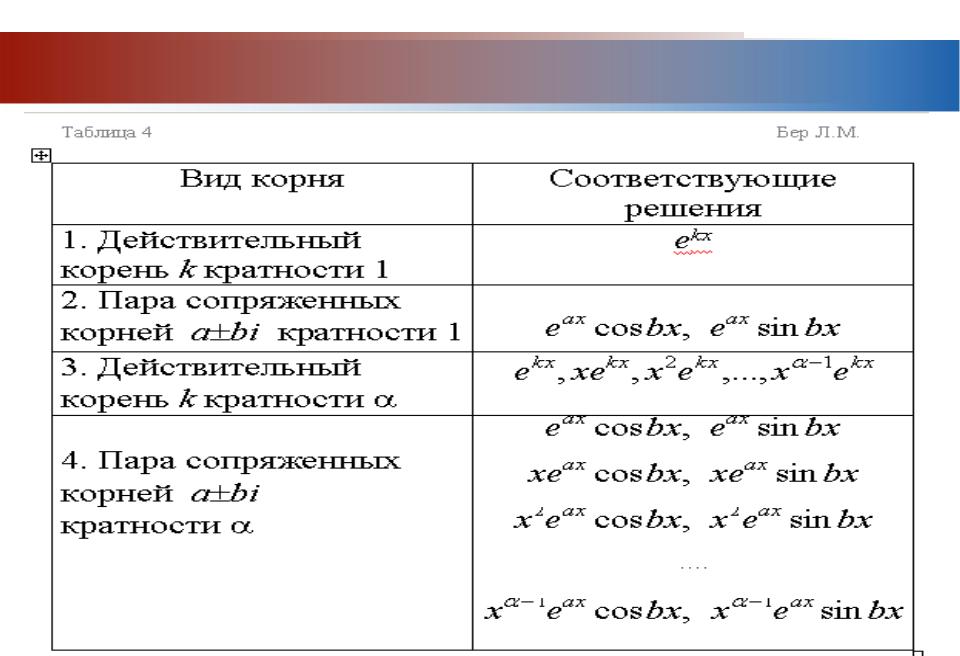
Алгоритм решения ЛОДУ n-го порядка с постоянными коэффициентами

1. Составить характеристическое уравнение (y =ekx).

2. Найти его корни k1, k2, …kn.

3. По характеру корней найти частные линейно

независимые решения y1(x), y2(x),… ,yn(x) согласно таблице 4.

4. Записать общее решение

y(x) = C1 y1(x) + C2 y2(x) +…+ Cn yn (x).

www.themegallery. com