1b). Вектор нормали прямой
,
|
направляющий вектор |
, |
|
угловой коэффициент |
|
46
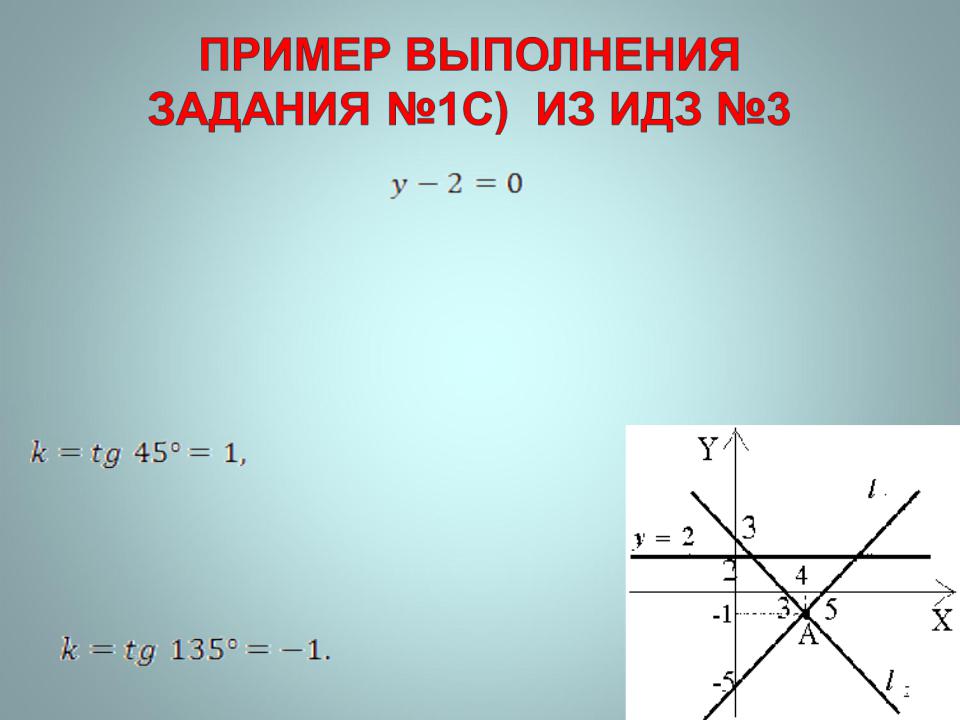
1c). Данная прямая является горизонтальной и составляет осью OX угол 0 градусов. Под углом 45 градусов к ней через
заданную точку можно провести две прямые, одна прямая будет составлять с осью OX угол 45 градусов и, следовательно, ее угловой коэффициент
|
а другая прямая |
|
составлять с осью OX угол 135 |
|
градусов и, следовательно, |
|
ее угловой коэффициент |
,
.
Используем уравнение прямой проходящей через фиксированную точку с угловым коэффициентом
|
Вектор нормали прямой |
, |
|
направляющий вектор |
угловой |
|
коэффициен |
|
|
|
|
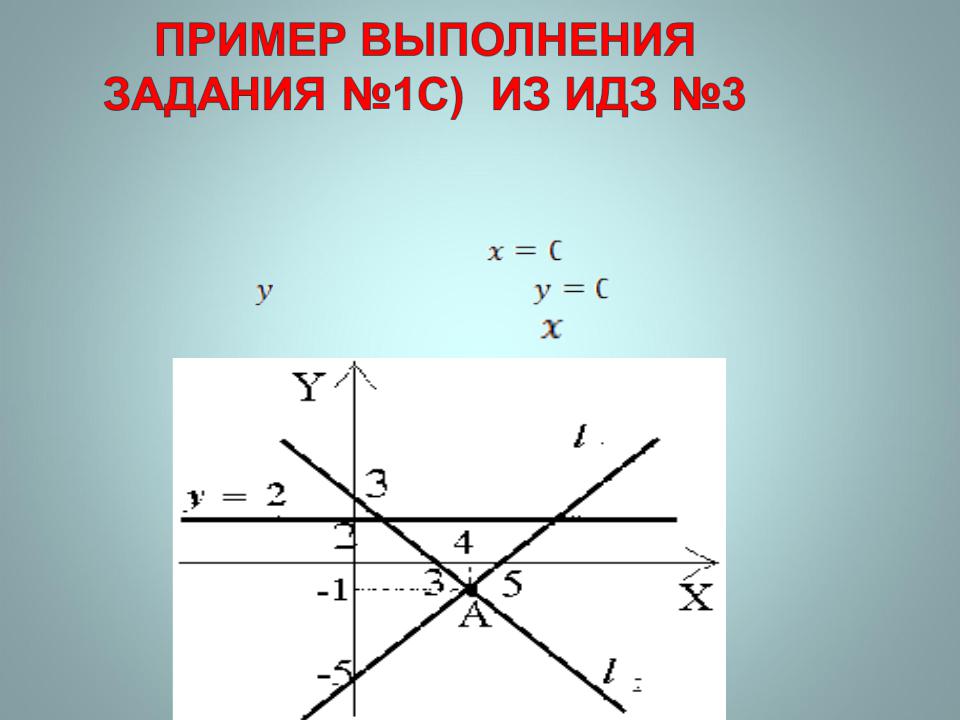
Для построения прямых в системе координат можно найти точки пересечения с осями
координат, взяв сначала |
и по |
|
уравнению вычислить |
, а затем взять |
. |
и вычислить соответствующее значение |
||
2. Даны две прямые
Найти: а) точку пересечения прямых,
b) косинус угла между прямыми,
с) уравнения биссектрис углов между прямыми.
|
Решение |
|
|
50
2a).Точкой пересечения прямых является решение системы
51
.
2b). Косинус угла между прямыми найдем как косинус угла между их нормальными векторами:
Для Для известен направляющий вектор
52
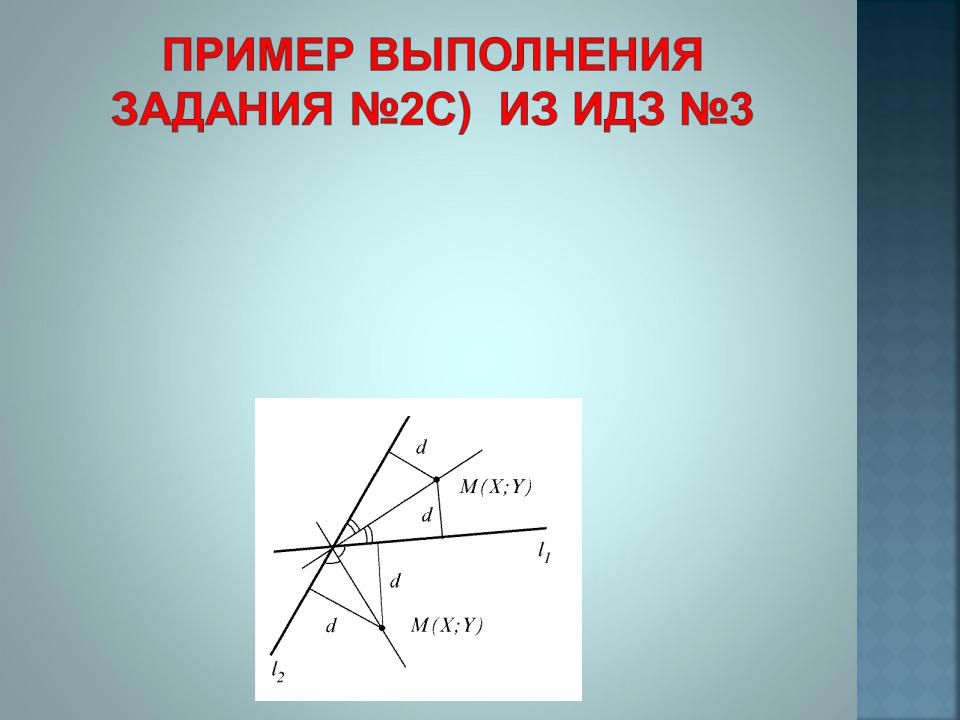
2c).Для составления уравнения биссектрисы угла между прямыми, а таковых две (острого и тупого угла), воспользуемся свойством, что любая точка биссектрисы равноудалена от сторон угла, то есть от прямых,
53
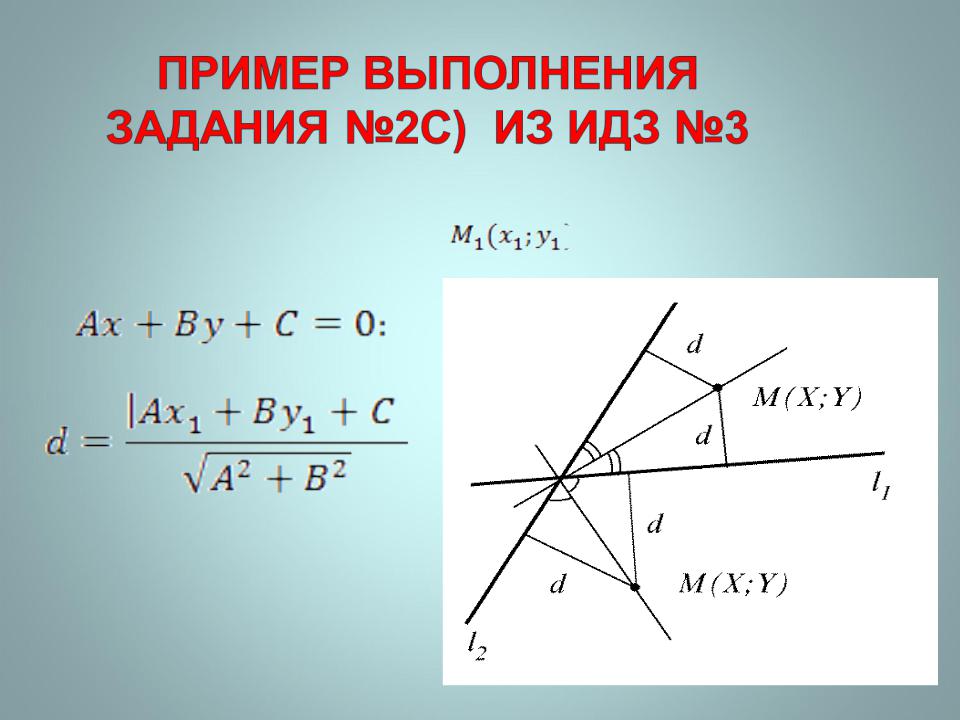
а также формулой для вычисления расстояния от точки до прямой
54
