
все лекции по самочерновой / КАБАНЛекции по Линейной алгебре (2 семестр)
.pdf
Аналитическая геометрия
Поверхностью в пространстве называется геометрическое место точек, декартовых координат которые удовлетворяют уравнению F(x,y,z)=0.
Линией на плоскости наз. геом. место точек, декартовых координат, которые удовлетворяют уравнению F(x,y)=0.
Линией в пространстве называют геометрическое место точек декартовых координат которые удовлетворяют уравнению F1(x,y,z)=0, F2(x,y,z)=0 – пересечение двух плоскостей.
Параметрическое задание поверхности и линии на плоскости.
x f1 (u, v)y f 2 (u, v)z f3 (u, v)
M(x,y,z) – сканирующая точка, которая перемещается по данной поверхности.
M(f1(u,v) ;f2(u,v) ;f3(u,v))
r OM { f1 (u, v), f 2 (u, v), f3 (u, v)} |
- параметрическое уравнение плоскости. |
||||||
|
Параметрическое уравнение линии на плоскости. |
||||||
x f1 (t) |
r |
OM |
{ f1 (t), f 2 (t)} |
|
|||
|
|
|
(t) |
|
|||
y f 2 |
|
|
|
|
|||
|
Параметрическое уравнение линии в пространстве. |
||||||
x f1 (t) |
|
|
|
|
|||
|
|
|
|
|
|
|
|
y f 2 |
(t) |
|
|
|
|
||
z f |
3 |
(t) |
r |
OM |
{ f1 (t), f 2 (t), f3 |
(t)} |
|
|
|
|
|||||
Алгебраические поверхности и линии на плоскости первого порядка.
Определение. Некоторое геометрическое место точек в пространстве (на плоскости) определяют плоскость (прямую на плоскости) тогда и только тогда, когда декартовы координаты x, y, z текущей точки М относительно некоторой декартовой системы координат удовлетворяют
алгебраическому уравнению первого порядка: |
|
|
|
|
Плоскость |
|
Прямая на плоскости: |
|
|
F (x, y, z) 0 |
|
F (x, y) 0 |
|
|
Ax By Cz D 0 |
|
Ax By C 0 |
|
|
M (x, y, z)OM r (x, y, z) |
|
M (x, y)OM r (x, y) |
|
|
N ( A, B, C) |
|
N ( A, B) |
|
|
(r, N ) Ax By Cz |
|
(r, N ) Ax By |
|
|
(r, N ) D 0 - общее уравнение плоскости в |
|
(r, N ) C 0 - общее уравнение прямой |
||
векторной форме. |
|
в векторной форме. |
|
|
Геометрический смысл нормального вектора |
|
|
||
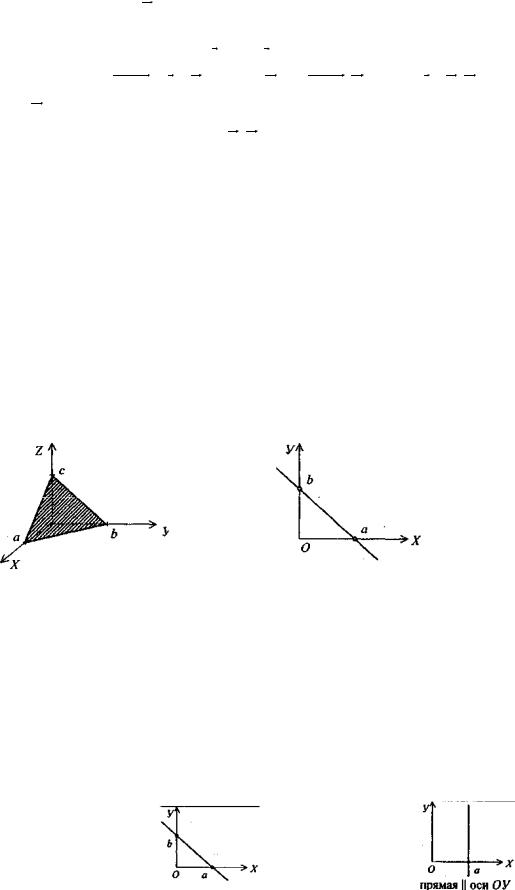
Пусть на плоскости дана фиксированная точка M 0 (r0 ) M 0 (x0 , y0 ) |
и |
|||
вектор N = (А, В). Составим уравнение прямой на плоскости, |
||||
проходящей через точку М0 |
перпендикулярно вектору N. |
M (x, y) |
r- |
|
радиус вектор точки, тогда |
|
|
|
|
M 0 M r r0 , M 0 M N (M 0 M , N) 0 (r r0 , N) 0 - |
уравнение |
|||
прямой в векторном виде. Тогда распишем это уравнение в
координатной форме:
A(x x0 ) B( y y0 ) 0 (r, N) Ax By,C (r0 , N) Ax0 By0
Определение. Вектор N, перпендикулярный прямой, называется нормальным вектором данной прямой. В качестве нормального вектора может быть взят любой вектор, перпендикулярный прямой.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть |
дана |
в |
пространстве |
|
|
|
фиксированная |
точка |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M 0 (r0 ) M 0 (x0 , y0 , z0 ) |
и вектор N = (А, В, C). Составим уравнение |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
прямой на плоскости, проходящей через точку М0 перпендикулярно |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вектору N. M (r) , где r (x, y, z) , тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M 0 M r r0 , M 0 M N (M 0 M , N) 0 (r r0 , N) 0 . |
|
||||||||||||||||||||
P : M 0 P, P N Тогда распишем это уравнение в координатной форме: |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
A(x x0 ) B( y y0 ) C(z z0 ) 0 D (r0 , N) Ax0 By0 Cz0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Вывод: нормальный |
|
|
|
вектор плоскости |
N |
= (A,B,C)-это |
|
любой |
|
вектор, |
который |
|||||||||||||||||||||||||||||
перпендикулярен искомой плоскости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнения в отрезках |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рассмотрим общие уравнения плоскости и прямой на плоскости: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
Ax By Cz D 0, D 0 |
|
|
|
Ax By C, C 0 |
|
||||||||||||||||||||||||||||||||||
|
x |
y |
|
|
z |
|
|
|
|
|
|
|
|
x |
|
y |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||||||||
|
|
D |
|
|
D |
|
D |
|
|
|
|
|
|
D |
|
|
|
D |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
A |
B |
|
|
|
C |
|
|
|
|
|
|
|
|
|
A |
|
B |
|
|
|
|
|
||||||||||||||||
|
a |
D |
, b |
D |
|
, c |
D |
|
|
|
|
a |
D |
|
, b |
D |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
A |
|
|
|
|
|
|
B |
|
|
C |
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
B |
|
||||||
|
|
|
|
|
|
|
x |
|
y |
|
z |
1 |
|
|
|
|
|
|
|
x |
|
y |
|
1 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
a |
|
|
b |
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
a |
|
b |
|
|
|
|
|
||||||||
Данные уравнения называются уравнениями в отрезка, т.к. прямая и плоскость отсекают от координатных прямых отрезки a,b, c и a,b соответственно.
Исследование общего уравнения прямой.
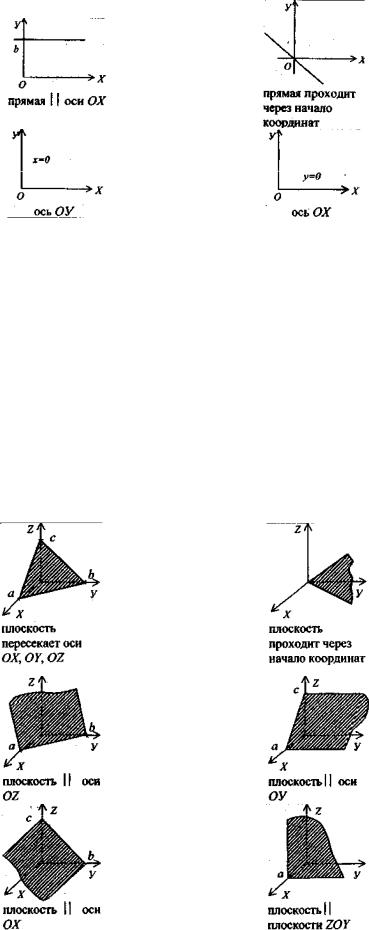
1.Если в уравнении прямой присутствуют все члены, то прямая пересекает координатные оси и отсекает от них отрезки a,b.
2.Если в уравнении прямой свободный член, то прямая проходит через начало координат.
3.Если в уравнении прямой отсутствует член, содержащий x или y, то прямая проходит параллельно оси отсутствующей координаты.
4.Если в уравнении прямой отсутствует член, содержащий x или y и свободный член, то прямая является осью ox или oy.
Вид уравнения |
Геометрическая |
Вид уравнения |
Геометрическая |
|||||||
иллюстрация |
иллюстрация |
|||||||||
|
|
|
|
|
|
|
|
|||
Ax By C 0 |
|
Ax C 0 |
|
|||||||
|
x |
|
y |
1 |
|
|
x |
1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
||||||
|
a b |
|
|
a |
|
|||||
|
|
A 0, B 0,C 0 |
|
|||||||
A 0, B 0,C 0 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
By C 0 |
|
Ax By 0 |
|
|||||||||
|
|
x |
|
|
|
y |
|
|||||
|
|
|
|
|
|
|
|
|
|
|||
|
y |
1 |
|
|
|
|
|
|
0 |
|
||
|
|
|
a |
b |
||||||||
|
|
|
||||||||||
|
b |
|
A 0, B 0,C 0 |
|
||||||||
A 0, B 0,C 0 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|||||||
Ax 0 |
|
|
|
By 0 |
|
|||||||
|
x |
|
|
|
|
y |
|
|||||
|
|
0 |
|
|
|
|
|
0 |
|
|||
|
a |
|
|
|
||||||||
|
|
|
|
|
b |
|||||||
A 0, B 0,C 0 |
|
A 0, B 0,C 0 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Исследование общего уравнения плоскости.
1.Если в уравнении плоскости присутствуют все члены, то плоскость пересекает координатные оси и отсекает от них отрезки a,b,c.
2.Если в уравнении плоскости отсутствует свободный член, то плоскость проходит через начало координат.
3.Если в уравнении плоскости отсутствует одна координата, то плоскость параллельна оси отсутствующей координаты.
4.Если в уравнении плоскости отсутствуют одна координаты и свободный член, то это есть плоскость проходящая через ось отсутствующей координаты
5.Если в уравнении плоскости отсутствуют две координаты, то плоскость параллельна координатной плоскости отсутствующей координаты.
6.Если в уравнении плоскости отсутствуют две координаты и свободный член, то это есть координатная плоскость отсутствующих координат.
Вид уравнения |
Геометрическая |
Вид уравнения |
Геометрическая |
|||||||||||||||||||
иллюстрация |
иллюстрация |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Ax By Cz D 0 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
x |
y |
z |
|
Ax By Cz 0 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
A 0, B 0, |
|
||||||||||
|
a |
b |
c |
|
|
|||||||||||||||||
|
A 0, B 0, |
|
C 0.D 0 |
|
||||||||||||||||||
|
C 0.D 0 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Ax By D 0 |
|
Ax Cz D 0 |
|
|||||||||||||||||||
|
|
|
x |
|
|
|
y |
|
|
|
|
x |
|
|
|
z |
|
|||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
a |
c |
|
|||||||||
|
|
|
a |
|
b |
|
|
|
||||||||||||||
|
A 0, B 0, |
|
A 0, B 0, |
|
||||||||||||||||||
|
C 0.D 0 |
|
C 0.D 0 |
|
||||||||||||||||||
|
|
|
|
|||||||||||||||||||
By Cz D 0 |
|
Ax D 0 |
|
|||||||||||||||||||
|
|
|
y |
|
|
|
z |
|
|
|
|
|
|
x |
|
|||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
||||||||||
|
|
|
b |
c |
|
|
|
|
||||||||||||||
|
A 0, B 0, |
|
A 0, B 0, |
|
||||||||||||||||||
|
C 0.D 0 |
|
C 0.D 0 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

By D 0 |
|
|
Cz D 0 |
|
||||||||
|
y |
1 |
|
|
|
|
z |
1 |
|
|||
|
|
|
|
|
|
|
|
|||||
|
b |
|
|
|
|
c |
|
|||||
A 0, B 0, |
|
|
A 0, B 0, |
|
||||||||
C 0.D 0 |
|
C 0.D 0 |
|
|||||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
By 0,Cz 0 |
|
||||||
Ax 0 |
|
|
y |
0, |
z |
0 |
|
|||||
|
x |
|
|
|
|
|||||||
|
|
|
b |
|
|
|
c |
|
||||
|
|
0 |
|
A 0, B 0, |
|
|||||||
|
a |
|
|
|||||||||
A 0, B 0, |
|
C 0.D 0 |
|
|||||||||
C 0.D 0 |
|
A 0, B 0, |
|
|||||||||
|
|
|
|
|
C 0.D 0 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Каноническое и параметрическое уравнения прямой на плоскости и в пространстве.
Пусть дана фиксированная точка М0 и вектор l. Выведем уравнения прямой на плоскости и в пространстве, проходящие через эту точку М0 параллельно вектору l.
Определение. Вектор, параллельный данной прямой или лежащий на этой прямой, называется направляющим вектором прямой.
На плоскости: |
В пространстве: |
M0(x0,y0) – фиксированная точка |
M0(x0,y0,z0) – фиксированная точка |
M (x,y)– текущая точка с перемен. |
M(x,y,z) – текущая точка с перемен. |
координатами |
координатами |
l=(m,n) направляющий вектор прямой |
l=(m,n,p) направляющий вектор прямой |
M 0 M r r 0 (x x0 , y y0 ) |
M 0 M r r 0 (x x0 , y y0 , z z0 ) |
Из условия коллинеарности векторов M 0 M tl r r0 tl r r0 tl - параметрическое
уравнение прямой на плоскости и в пространстве. Запишем это уравнение в координатной форме, а затеи исключим параметр t:
x x0 tm |
|
|
x x0 tm |
||||||||
|
|
|
|
|
|
|
|
|
tn |
||
y y0 tn |
|
|
y y0 |
||||||||
|
|
|
|
|
|
z z |
0 |
tp |
|||
x x0 |
y y0 |
|
|
|
|
|
|
|
|||
|
x x0 |
|
y y0 |
|
z z0 |
||||||
m |
|
n |
|
|
|
||||||
|
|
|
|
|
|||||||
|
|
|
|
|
m |
|
n |
|
|
p |
|
Мы получили каноническое уравнение прямой на плоскости и в пространстве. Из канонического уравнения можно получить уравнения прямой, проходящей через 2
фиксированные точки (M1 и M2):
M1(x1,y1), M2(x2,y2) – фиксированные точки |
M1(x1,y1,z1), M2(x2,y2,z2) – фиксированные |
||||||||||||||||
M (x,y)– текущая точка с перемен. |
точки |
|
|
|
|
|
|
|
|
|
|||||||
координатами |
M (x,y,z)– текущая точка с перемен. |
||||||||||||||||
M1M2=(x2-x1,y2-y1) M1M=(x-x1,y-y1) |
координатами |
|
|
|
|
|
|||||||||||
M1M=(x-x1,y-y1) |
M1M2=(x2-x1,y2-y1,z2-z1) |
||||||||||||||||
M1M2// M1M их координаты |
M1M=(x-x1,y-y1,z-z1) |
|
|
|
|||||||||||||
пропорциональны |
M1M2// M1M их координаты |
||||||||||||||||
|
x x1 |
y y1 |
пропорциональны |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
x x1 |
|
y y1 |
|
z z1 |
|
||||||
|
x2 x1 |
y2 y1 |
|||||||||||||||
|
|
x |
2 |
x |
y |
2 |
y |
z |
2 |
z |
|||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
1 |
|
|||
Выводы: Для составления уравнения прямой на плоскости необходимо знать:
1.Фиксированную точку М0(х0,у0) и нормальный вектор прямой N = (А, В), перпендикулярный данной прямой.
2.Фиксированную точку М0(х0,у0) и направляющий вектор l =(m,n), параллельный данной прямой;
3.Две фиксированные точки M1(x1,y1), M2(x2,y2)
4.Фиксированную точку М0(х0,у0) и тангенс угла наклона k tg , образованный прямой с осью ОХ;
5.значения отрезков, отсекаемых прямой от координатных осей.
Для составления уравнения прямой в пространстве необходимо знать:
1.Фиксированную точку М0(х0,у0,z0) и направляющий вектор l =(m,n,p), параллельный данной прямой;
2.Две фиксированных точки M1(x1,y1,z1), M2(x2,y2,z2).
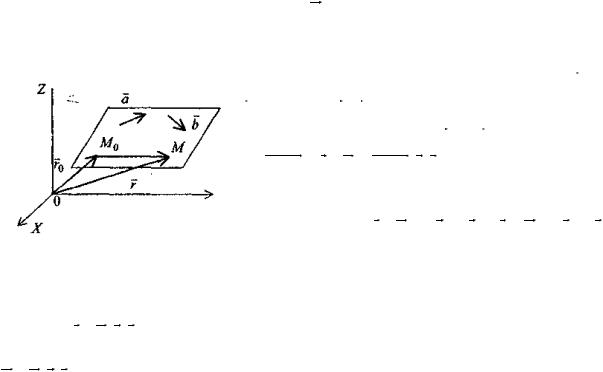
Параметрическое уравнение плоскости
Пусть дана фиксированная точка M 0 (r0 ) и два неколлинеарных вектора а и b. Выведем уравнение плоскости, проходящей через точку M 0 параллельно векторам а и b. Векторы а и b можно параллельным переносом опустить в искомую плоскость как свободные векторы.
M 0 (x0 y0 z0 ) |
фиксированная точка |
a (a1 , a2 , a3 ) |
b (b1 ,b2 ,b3 )(a || b) |
M (x, y, z) точка с переменными |
|
координатами. P {McP, P || a, P || b} |
|
|
M 0 M r r0 |
M 0 M , a,b - лежат в одной плоскости, т.е. |
|
они компланарны, они являются линейно зависимыми и один из них выражается является линейной комбинацией
остальных: r r0 pa qb r r0 pa qb -
параметрическое уравнение плоскости в векторной форме.
|
x x0 pa1 qb1 |
||||
Запишем полученное уравнение в координатной форме: |
|
|
pa2 |
qb2 |
|
y y0 |
|||||
|
z z |
0 |
pa |
3 |
qb |
|
|
|
3 |
||
Векторы r r0 , a,b компланарны, |
следовательно, их смешанное произведение равно 0: |
||||||
(r r0 , a, b) 0 |
|
x x0 |
y y0 |
z z0 |
|
0 |
|
|
|
||||||
|
a1 |
a2 |
a3 |
|
|
||
|
|
b1 |
b2 |
b3 |
|
|
|
Выведем уравнение плоскости, проходящей через три точки M1,M2,M3. Возьмем на плоскости текущую точку M(x,y,z) и составим три компланарных вектора M1M2, M1M, M1M3.
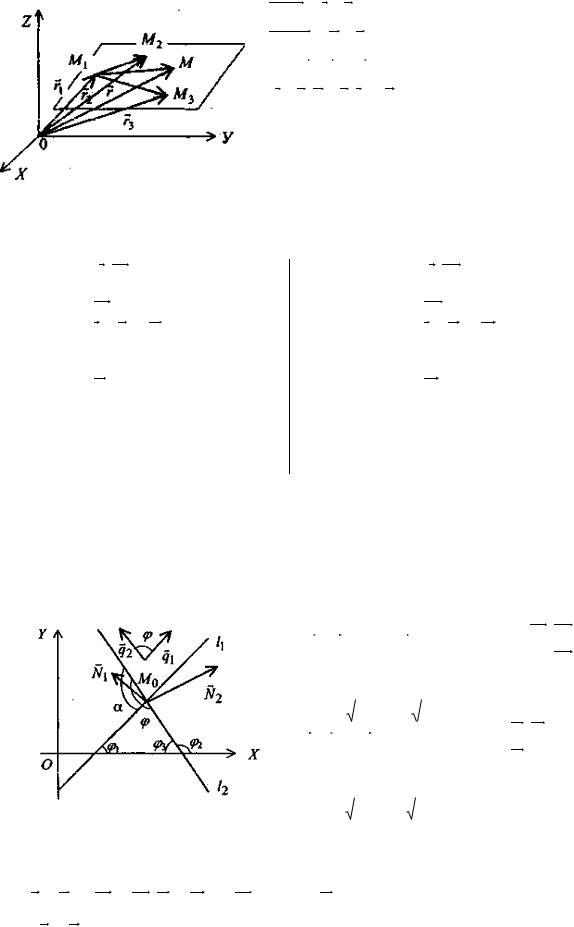
M1M r r1 (x x1 , y y1 , z z1 )
M1M 2 r2 r1 (x2 x1 , y2 y1 , z2 z1 )
M1M 3 |
r 3 r1 (x3 x1 , y3 y1 , z3 z1 ) |
|||
(r r1 , r2 r1 , r 3 r1 ) 0 |
|
|||
|
x x1 |
y y1 |
z z1 |
|
|
|
|||
|
x2 x1 |
y2 y1 |
z2 z1 |
0 |
|
x3 x1 |
y3 y1 |
z3 z1 |
|
Взаимное расположение прямых на плоскости.
Пусть даны две прямые на плоскости, заданные своими уравнениями:
(r, N1 ) C1 0
A1 x B1 y C1 0
N1 ( A1 , B1 ), N1 l1
r r1 |
tq1 |
|||
x x1 |
l1t |
|||
y y |
m t |
|||
|
|
1 |
1 |
|
q1 |
(l1, m1 ) || l1 |
|||
x |
x1 |
|
y y1 |
|
|
l1 |
m1 |
||
|
|
|
||
y k1 x b1 , k1 tg 1
(r, N 2 ) C2 0
A2 x B2 y C2 0
N 2 ( A2 , B2 ), N 2 l2
r r2 |
tq2 |
|||||
x x2 |
l2t |
|||||
|
y2 |
m2t |
||||
y |
||||||
q2 |
(l 2 , m2 ) || l2 |
|||||
x x2 |
|
y y2 |
|
|||
l2 |
m2 |
|||||
|
|
|||||
y k2 x b2 , k2 tg 2
- уравнения с угловыми коэффициентами.
Найдем:1)угол между прямыми 2)условие перпендикулярности прямых.
3)условие параллельности прямых.
4)yравнение прямой l, проходящей через точку M0 пересечения двух прямых l1 и l2.
1.Найдем угол между прямыми l1 и l2, как угол между N1, N2 или направляющими векторами q1, q2.
(N1 , N 2 ) |
|
N1 |
|
N 2 |
|
cos cos |
(N1 , N |
2 ) |
||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
N1 |
|
N 2 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
cos |
|
|
|
|
|
|
A1 A2 B1 B2 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
A2 B 2 |
|
|
|
A2 |
B 2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
1 |
1 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
(q1 , q2 ) |
|
q1 |
|
q2 |
|
cos cos |
(q1 , q2 ) |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
q1 |
|
q2 |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
cos |
|
|
|
|
|
|
l1l2 m1m2 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l 2 |
m2 |
|
|
l 2 m2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
1 |
|
|
1 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Если k tg , k |
|
tg |
|
, тогда |
|
tg tg |
|
|
tg 2 tg 1 |
tg |
k2 k1 |
. |
|||||||||||
2 |
2 |
2 |
2 |
|
|
||||||||||||||||||
|
1 |
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
1 |
tg 1tg 2 |
1 k2 k1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2. |
Условие перпендикулярности прямых. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Если l1 l2 |
N1 N2 , q1 |
q2 |
(N1 , N2 ) 0, (q1 , q2 ) 0 |
|
|
|
|
|
|
|
|
||||||||||||
l |
l |
|
90 ,tg 1 k k |
|
0 k |
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
||||||||||||
1 |
|
|
|
|
|
|
1 |
|
|
|
k1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3. |
Условие параллельности прямых. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Если l || l |
|
N |
|
|| N |
, q || q |
|
N |
|
N |
, q |
q |
|
|
A1 |
|
B1 |
, |
l1 |
|
m1 |
, k |
k |
|
2 |
1 |
2 |
1 |
2 |
|
|
|
|
2 |
||||||||||||||
1 |
|
2 |
1 |
|
2 |
1 |
|
|
A2 |
|
B2 |
|
l2 |
|
m2 |
1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
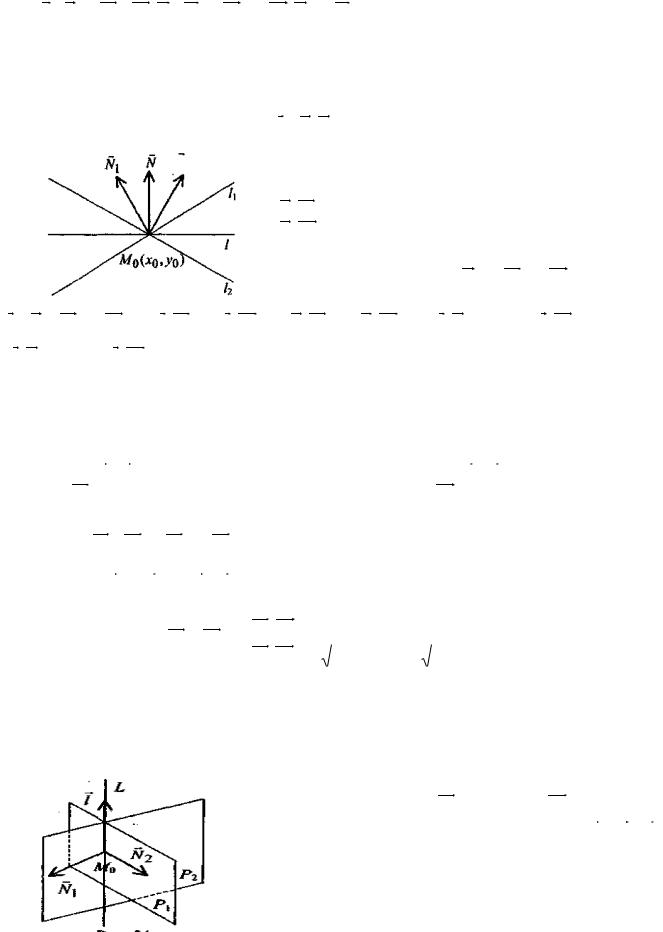
4. Уравнение прямой l, проходящей через точку M0 пересечения двух прямых l1 и l2.
Определение. Совокупность всех прямых плоскости, проходящих через фиксированную точку M0, называется пучком прямых.
Уравнение прямой l будем искать как уравнение прямой, проходящей через фиксированную
точку M0 |
перпендикулярно вектору N. (r r0 , N ) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для этого найдем координаты точки M0 как пересечения |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
двух прямых l1и l2. Для этого решим систему двух |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
уравнений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r , N |
1 |
C 0 |
|
A x |
0 |
B y |
0 |
C |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
1 |
|
|
|
1 |
|
|
1 |
|
|
1 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r , N |
2 |
C |
2 |
0 |
|
A2 x0 |
B2 y0 C2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Векторы N,N1,N2 |
|
|
компланарны, |
следовательно они |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
линейно |
|
зависимы, |
|
тогда |
N N1 |
N2 |
подставим в |
||||||||||||||||||||
r r0 , N1 N2 |
r, N1 r, N2 |
уравнение прямой l |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
r0 , N1 |
r0 , N2 (r, N) C1 (r, N2 ) C2 0 |
|||||||||||||||||||||||||||||||||||||||||||
(r, N ) C1 (r, N2 ) C2 |
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
- уравнения пучка прямых. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
( A1 x B1 y C1 ) ( A2 x B2 y C2 ) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Взаимное расположение плоскостей в пространстве |
|
||||||||||||||||||||||||||||||||||
|
Пусть даны две плоскости: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
P1 : (r, N1 ) D1 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P2 : (r, N 2 ) D2 0 |
|
||||||||||||||
|
|
N1 ( A1 , B1 |
, C1 ) P1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N 2 |
( A2 , B2 , C2 ) P2 |
||||||||||||||
|
|
A1 x B1 y C1 z D1 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 x B2 y C2 z D2 |
0 |
|||||||||||||||||
1. P || P N || N |
|
N N |
|
|
A1 |
|
B1 |
|
C1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
1 |
2 |
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
A2 |
|
|
B2 |
|
|
|
C2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2. P P N |
1 |
N |
2 |
(N |
, N |
2 |
) 0 A A B B C C |
2 |
0 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
1 |
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
2 |
|
|
1 |
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3. Угол между P1 |
и P2 |
равен углу между нормальными векторами N1 |
и N2: |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
cos(N1 N2 ) |
(N1 , N2 ) |
|
|
|
|
|
|
A1 A2 B1 B2 C1C2 |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
N |
1 |
N |
2 |
|
|
|
|
|
A2 |
B2 |
C |
2 |
|
A2 |
B2 |
C 2 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
1 |
|
|
|
2 |
2 |
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Параметрическое и каноническое уравнения прямой, заданной пересечением двух плоскостей.
Прямая линия в пространстве может быть получена в результате пересечения двух плоскостей:
A1 x B1 y C1 z D1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
L : A x B |
2 |
y C |
2 |
z D |
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
Плоскость P1 и P2 |
могут пересечься лишь в том случае, когда их |
||||||||||||
|
|
|
|
|
|
нормальные |
|
|
векторы |
N1 A1 , B1 ,C1 , N2 A2 , B2 ,C2 |
|||||||||
|
|
|
|
|
|
неколлинеарны. Параметрическое уравнение прямой r r0 tl . |
|||||||||||||
|
|
|
|
|
|
Чтобы найти координаты фиксированной точки M0, |
|||||||||||||
|
|
|
|
|
|
принадлежащей прямой, надо решить совместно систему: |
|||||||||||||
|
|
|
|
|
|
A1 x0 |
B1 y0 |
C1 z0 |
|
D1 |
0 |
|
|||||||
|
|
|
|
|
|
A x |
0 |
B |
2 |
y |
0 |
C |
2 |
z |
0 |
D |
0 . |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|||||
Так как ранг этой системы равен 2, то система имеет бесконечное множество решений и любое частное решение определяет координаты точки M0. Найдем направляющий вектор l

прямой. l N1 ,l N2 , тогда в качестве направляющего вектора можно взять вектор
l N1 , N 2 |
i |
j |
k |
|
Тогда параметрическое уравнение прямой L: r r0 t N1 , N2 . |
|||||||
A1 |
B1 |
C1 |
|
|||||||||
|
A2 |
B2 |
C2 |
|
|
|
|
|
|
|
|
|
Предположим, что x0,y0 базисные неизвестные, а свободный член z0=0, то |
||||||||||||
A1 x0 B1 y0 D1 |
|
|
x x0 |
|
y y0 |
|
|
x x0 |
tl1 |
|||
|
|
|
|
z |
|
|
||||||
|
D2 |
|
|
|
|
|
|
y y0 |
tl2 , M 0 (x0 , y0 ,0) |
|||
l1 |
l2 |
l3 |
||||||||||
A2 x0 B2 y0 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
z tl3 |
|
|
5.Уравнение пучка плоскостей.
Найдем теперь уравнение плоскости Р, проходящей через прямую пересечения Р1 и Р2.
Будем искать |
уравнение плоскости Р в виде (r r0 , N ) 0 . |
Векторы N1 , N2 , N L , |
|
следовательно, они компланарны, т.е. линейно зависимы и |
N N1 |
N 2 . |
|
Уравнение |
плоскости |
|
P: |
(r r0 , N1 N2 ) (r, N1 ) D1 (r, N2 ) D2 0 (r, N1 ) D1 (r, N2 ) D2 0,
. – уравнение пучка плоскостей.
6.Пересечение трех плоскостей.
Даны три плоскости P1,P2,P3. Найдем точку пересечения трех плоскостей:
A x B y C z D 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
1 |
1 |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P : A2 x |
B2 y C2 z D2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
A x B y C |
z D |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
3 |
3 |
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 |
|
B1 |
C1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Если M 0 |
P1 |
P2 |
P3 |
A2 |
|
B2 |
C2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
A3 |
|
B3 |
C3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Найдем уравнение плоскости проходящей через точку M |
0 |
, P :{M |
0 |
P, M |
0 |
P P P } |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
3 |
||||
N1 , N2 , N3 не компланарны N 1 N1 2 |
N2 3 N3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
P : (r r |
|
, N ) (r r |
|
, |
N |
|
|
|
N |
|
|
|
N |
) 0 (r r , N |
) |
2 |
(r r , N |
|
) |
3 |
(r r , N |
) 0 |
||||||||||||
0 |
0 |
1 |
2 |
2 |
3 |
|
2 |
|
||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
3 |
0 |
1 |
|
|
|
1 |
|
|
0 |
|
|
1 |
0 |
3 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Чтобы найти точку пересечения трех плоскостей, нужно решить систему трех уравнений этих плоскостей. При решении системы могут быть следующие случаи:
1.rangA=rangA*=3 Система совместна, определена, имеет единственное решение M0
(x0,y0,z0).
2.rangA=2 rangA*=3 Система несовместна. С геометрической точки зрения это значит, что две плоскости пересекаются по прямой, которая параллельна третьей плоскости, т.е. не существует точки, которая принадлежала бы всем трем плоскостям.
3.rangA=rangA*=2 В этом случае одно из уравнений системы есть линейная комбинация двух остальных. Это значит, что всякая точка, принадлежащая двум плоскостям, необходимо принадлежит и третьей, т.е. все три плоскости проходят через одну прямую.
4.rangA=1 rangA*=2 Система несовместна. Геометрически этот случай означает, что все три плоскости параллельны между собой.
5.rangA=rangA*=1 В этом случае все три уравнения определяют одну плоскость.
Взаимное расположение прямой и плоскости
Пусть дана плоскость Р: (r, N) D 0 Ax By Cz D 0, N (A, B,C) P и прямая L:
|
x x |
tl |
|
l l ,l |
|
|
|| L |
|
r r tl |
y y0 |
tl1 |
2 |
, l |
||||
0 |
|
0 |
tl |
2 |
1 |
3 |
|
|
|
z z |
0 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||

1.Угол между прямой и плоскостью (L^ P) (L^ L ) L’ – любая прямая, проходящая через точку M0.
2 , (N ^ l)
|
|
|
|
|
|
|
|
|
sin |
|
|
|
cos |
|
|
|
(N , l) |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
l |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Условие |
|
|
|
|
|
|
прямой |
|
и |
плоскости. |
||||||||||||
|
L P N || l N l |
A |
|
B |
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
l1 |
l2 |
|
l3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
Условие |
параллельности |
прямой |
и |
плоскости |
|||||||||||||||||
L || P N l (N,l) Al1 Bl2 Cl3 0
4.Точку пересечения прямой и плоскости. Чтобы найти точку пересечения прямой L с
плоскостью P, подставим радиус-вектор текущей точки прямой r=r0+tl в уравнение плоскости:
(r, N ) D 0 (r0 tl, N ) D 0 (r0 , N ) t(l, N ) D 0 t D (r0 , N )
Тогда |
радиус-вектор |
точки |
пересечения |
прямой |
и |
плоскости |
имеет |
|||
вид: r r0 |
tl r0 |
|
D (r0 |
, N ) |
l |
|
|
|
|
|
(l, N ) |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
t |
Ax0 By0 Cz0 D |
. Для параметра t возможны следующие случаи: |
|||||||
Al1 |
Bl2 |
Cl3 |
|||||||
|
|
|
|
|
|
||||
1) Al1 Bl2 |
Cl3 |
0, Ax0 |
By |
0 |
Cz0 D 0 , |
тогда прямая не имеет ни одной общей точки с |
|||
плоскостью. 2) |
Al1 Bl2 |
Cl3 |
0, Ax0 By |
0 |
Cz0 D 0 , тогда параметр t может принимать |
||||
любое значение. В этом случае эта прямая проходит через точку M0, лежащую на плоскости, следовательно вся прямая L лежит в плоскости.
5. Условие принадлежности прямой L и плоскости P. Необходимым и достаточным условием принадлежности прямой L плоскости P является выполнение равенств:
|
(N.l) 0 Al1 Bl2 Cl3 0 |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
(N, r ) d 0, Ax |
0 |
By |
0 |
Cz |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Взаимное расположение прямых в пространстве. |
|
|
|
||||||||||||||
Пусть в пространстве две прямые заданы уравнениями: |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
L1 : r r1 l1t |
L2 : r r 2 l2t |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
l1 (a1 , b1 , c1 ) || L1 |
l2 (a2 , b2 , c2 ) || L2 |
|
|
|
|
|
|||||||||
1. |
Условие параллельности прямых L |
|| L |
l |
// l |
|
[l ,l |
|
] 0 |
a1 |
|
b1 |
|
c1 |
|
||||||
2 |
2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
1 |
2 |
1 |
|
1 |
|
a2 |
|
b2 |
|
c2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2. |
Условие |
|
|
|
|
|
перпендикулярности |
|
|
|
|
|
|
|
прямых |
|||||
L1 L2 l1 l2 (l1 ,l2 ) 0 a1a2 b1b2 c1c2 0
3.Условие принадлежности двух прямых одной плоскости. Пусть прямые L1, L2
принадлежат плоскости P
тогда найдем M1M 2 r2 r1 x2 x1 , y2 y1 , z2 z1 . Векторы l1,l2,M1,M2 являются компланарными, и их
смешанное произведение равно нулю: (r2 r1 ,l1 ,l2 ) 0 .
Следовательно, для того, чтобы прямые L1 и L2 лежали в одной плоскости, необходимо и достаточно, чтобы их
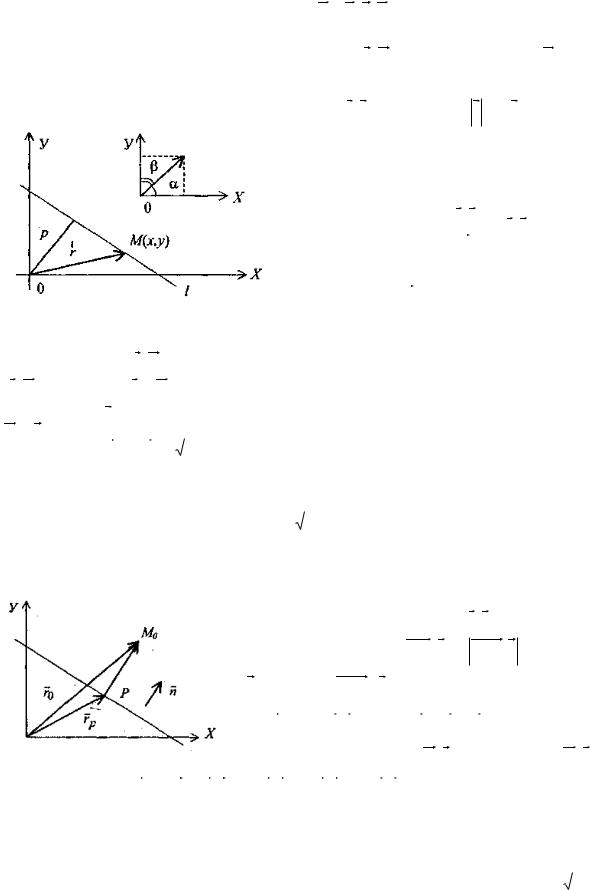
смешанное произведение |
было |
равно нулю. В |
||||
координатной форме |
|
x2 x1 |
y2 y1 |
z2 z1 |
|
. |
|
|
|||||
|
a1 |
b1 |
c1 |
|
||
|
|
a2 |
b2 |
c2 |
|
|
4. Условие, когда прямые являются скрещивающимися. Скрещивающиеся прямые в одной плоскости не лежат, следовательно, (r2 r1 ,l1 ,l2 ) 0 .
Расстояние от точки до прямой на плоскости
Пусть задана прямая на плоскости l уравнением (r, N ) C 0 и точка M 0 (r0 ) l . Требуется найти расстояние (M 0 ,l) . Для нахождения расстояния от точки до прямой используется
нормальное уравнение прямой, которое имеет вид (r, n) p 0, p 0, n 1, n l .
Особенностью нормального уравнения является то, что свободный член всегда отрицателен. Выясним смысл свободного члена р. Возьмем на заданной прямой текущую точку М(х.у), соединим ее с началом координат радиус-
вектором r и найдем пр |
|
|
(r |
, n) |
(r, n) p . Получили, что |
|
n |
|
n |
|
|||
|
|
|
||||
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– это расстояние от начала координат до прямой. Вектор можно задать через n cos , cos .
Тогда нормальное уравнение прямой имеет вид x cos y cos p 0 . Покажем, что общее уравнение прямой всегда можно привести к нормальному виду. Пусть прямая l задана общим уравнением (r, N ) C 0 . Умножим его на некоторый множитель
(r, N) C 0 (r, N) C 0 , сравним это уравнение с нормальным уравнением
N n |
|
|
|
|
|
|
n |
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
. μC=-p, следовательно, знак μ должен быть |
|||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
N |
|
|
|
N |
|
|
A2 B 2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
противоположным знаку свободного члена С общего уравнения прямой. Окончательно
нормирующий множитель имеет вид: |
|
1 |
|
. |
|
|
|
|
|||
|
|
|
|||
A2 B 2 |
|||||
|
|
|
|
Вывод: Чтобы общее уравнение прямой привести к нормальному виду нужно умножить его на множитель, обратный по величине модулю нормального вектора N и имеющий знак, противоположный знаку свободного члена.
Найдем теперь расстояние от фиксированной точки M0 до прямой l, заданной уравнением (r, n) p 0 Векторы PM, n
коллинеарны. Найдем (PM , n) PM 0 
 n cos .
n cos .
|
n |
|
1 (PM 0 |
0 |
, cos 1 |
, то получим, что |
|
|
|
||||||
|
|
^ n) |
|||||
|
|
|
|
|
180 |
|
|
|
|
|
|
|
|
||
|
PM 0 |
(PM 0 , n) , но PM 0 |
r0 rp и так как точка P |
||||
|
|
|
|
|
|
|
|
принадлежит прямой, то (rp , n) p 0 p (rp , n) .
Тогда (M 0 ,l) |
PM 0 |
|
(r0 rp , n) |
|
(r0 , n) (rp , n) |
|
(r0 , n) p |
. |
|
|
|
|
|
|
|
|
|
Вывод: Чтобы найти расстояние от точки M0 до прямой l нужно: 1)привести уравнение прямой к нормальному виду 2)в нормальное уравнение прямой подставить вместо x и y
координаты точки M0 и результат взять по модулю. В координатной форме: |
|
Ax0 |
By0 |
C |
|
. |
|
|
|
||||||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
A2 B 2 |
|
|||||
|
|
|
|
|
|||
