
- •Аналитическая геометрия – раздел геометрии, в котором
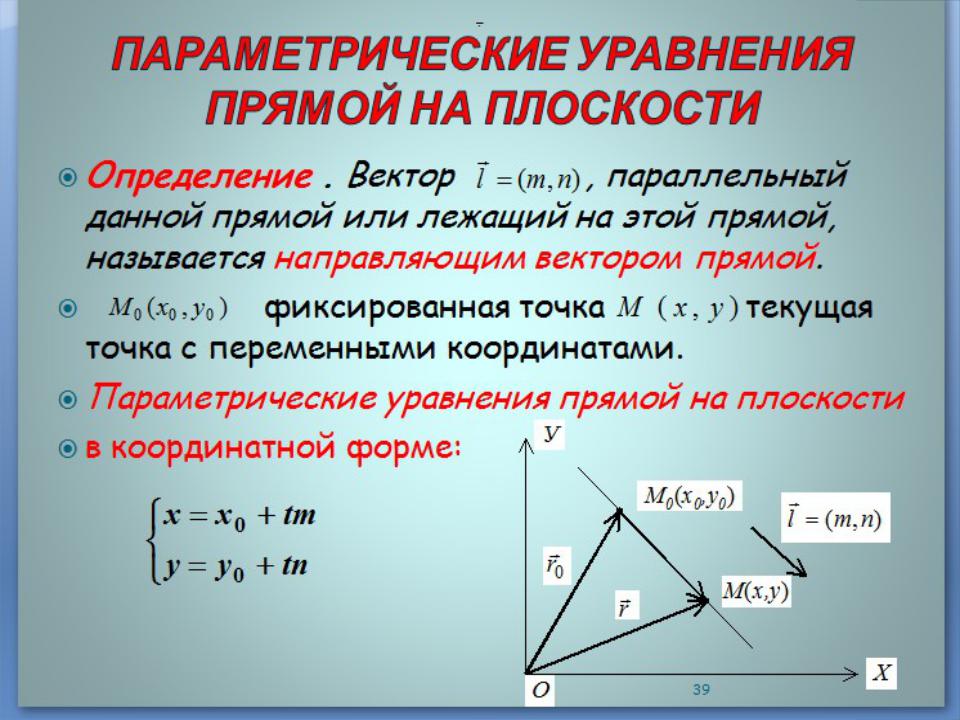
- •§1. ПРЯМАЯ НА ПЛОСКОСТИ
- •Определение . Некоторое геометрическое место точек на
- •1. Общее уравнение прямой на плоскости и его исследование
- •ИССЛЕДОВАНИЕ ОБЩЕГО УРАВНЕНИЯ ПРЯМОЙ
- •ИССЛЕДОВАНИЕ ОБЩЕГО УРАВНЕНИЯ ПРЯМОЙ.
- •2) Пусть в общем уравнении прямой коэффициенты
- •3)Пусть в общем уравнении прямой один из коэффициентов A или B – нулевой,
- •4) Пусть в
- •Замечание. Пусть прямая ℓ не проходит через O(0;0).
- •2. Другие формы записи уравнения прямой на плоскости
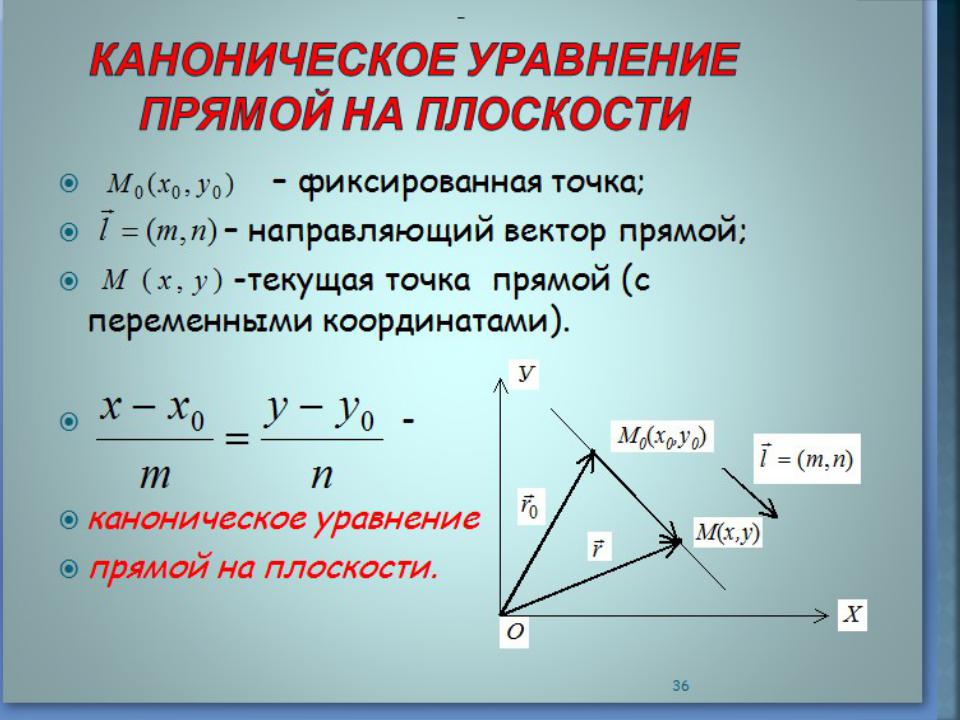
- •2) Каноническое уравнение прямой на плоскости
- •4) Уравнение прямой с угловым коэффициентом
- •Пусть прямая
- •ЛЕКЦИЯ №2
- •3. Взаимное расположение прямых на плоскости
- •1) Пусть прямые параллельны:
- •2) Пусть прямые пересекаются
- •4. Расстояние от точки до прямой
- •ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ НА ПЛОСКОСТИ
- •ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ НА ПЛОСКОСТИ
- •ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ НА ПЛОСКОСТИ
- •§ 2. ПЛОСКОСТЬ
- •Некоторое геометрическое место
- •1. Общее уравнение плоскости и его исследование
- •Уравнение плоскости, проходящей через фиксированную точку M 0 (x0 , y0 , z0
- •Уравнения
- •ИССЛЕДОВАНИЕ ОБЩЕГО УРАВНЕНИЯ ПЛОСКОСТИ
- •ИССЛЕДОВАНИЕ ОБЩЕГО УРАВНЕНИЯ ПЛОСКОСТИ
- •2)Пусть в общем уравнении плоскости коэффициенты A, B и C – ненулевые, а
- •3)Пусть в общем уравнении плоскости один из коэффициентов A, B или C –
- •б) плоскость отсекает на осях
- •4) Пусть в уравнении плоскости (2) два из трех коэффициентов A, B или
- •б) плоскость отсекает на Oy отрезок b и параллельна осям Ox и Oz
- •6) Пусть в общем уравнении плоскости (2)
- •Замечание. Пусть плоскость λ не проходит через O(0;0;0).
- •2. Другие формы записи уравнения плоскости
- •Уравнения
- •2)Уравнение плоскости, проходящей через три точки, не лежащие на одной прямой – частный
- •3. Взаимное расположение плоскостей
- •1) Пусть плоскости параллельны:
- •2) Пусть плоскости пересекаются
- •Частный случай – плоскости перпендикулярны, т.е.
- •4. Расстояние от точки до плоскости
- •стр.177, ФиксЧ.1
- •§ 3. ПРЯМАЯ В ПРОСТРАНСТВЕ
- •Прямая в пространстве
- •Другие формы записи уравнений прямой в пространстве – ПАРАМЕТРИЧЕСКИЕ и КАНОНИЧЕСКИЕ уравнения.
- •Уравнение
- •Частным случаем канонических уравнений являются УРАВНЕНИЯ ПРЯМОЙ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ДВЕ ЗАДАННЫЕ ТОЧКИ.
- •2. Переход от общих уравнений прямой к каноническим
- •3. Взаимное расположение прямых в пространстве
- •2) Пусть прямые ℓ1 и ℓ2 пересекаются:
- •4. Задачи, связанные с возможным взаимным расположением прямых
- •ЗАДАЧА 2. Найти угол между пересекающимися (скрещива- ющимися) прямыми в пространстве.
- •Пусть дана прямая
- •Пусть даны две скрещивающиеся прямые:
- •Пустьданыдвепересекающиесяпрямые
- •5. Взаимное расположение прямой и плоскости в пространстве
- •Частным случаем пересечения прямой и плоскости в одной точке является перпендикулярность прямой и
- •ОПРЕДЕЛЕНИЕ. Углом между прямой ℓ и плоскостью λ
- •Раздел 3.
- •Указать нормальный вектор прямой:
- •Составить уравнения прямой, проходящей через две фиксированные точкиM1 (3, 2) M 2 (
- •1b). Вектор нормали прямой
- •1c). Данная прямая является горизонтальной и составляет осью OX угол 0 градусов. Под
- •Для построения прямых в системе координат можно найти точки пересечения с осями
- •2. Даны две прямые
- •2a).Точкой пересечения прямых является решение системы
- •2c) . Даны две прямые
- •а также формулой для вычисления расстояния от точки до прямой
- •Приведем уравнение
- •Нетрудно заметить, что полученные уравнения биссектрис определяют перпендикулярные прямые.
- •3.Привести уравнения линий к каноническому виду и построить:
- •3.1. Полученное уравнение определяет окружность с центром
- •Полученное уравнение определяет эллипс с центром
- •3.3) Преобразуем уравнение линии
- •Раздел 4.
- •Определение. Поверхностью в
- •Некоторое геометрическое место
- •Уравнение плоскости, проходящей через фиксированную точку M 0 (x0 , y0 , z0
- •Вывести уравнение плоскости , проходящей через точкуM 0 ( 1,2, 2) перпендикулярно вектору
- •1.а).Составить уравнение плоскости, которая проходит : через точку параллельно двум векторам
- •Решение №1а) (продолжение)
- •Уравнение плоскости, проходящей
- •Уравнение плоскости в отрезках:
- •№1d) . Составить уравнение плоскости,
- •Определение . Векторl (m, n, p)
- •Каноническое уравнение прямой в пространстве в координатной форме:
- •Составить каноническое и параметрическое
- •№ 1.c) Составить уравнение плоскости, которая проходит через точку
- •Уравнение прямой, проходящей через 2 фиксированные точкиM1 (x1 , y1 , z1 ),
- •№2 b) . Составить канонические уравнения прямых, которые проходят
- •№2.c) Составить канонические уравнения прямых, которые проходят через точку
- •Направляющие косинусы указанного направления, которые являются координатами единичного вектора направления, удовлетворяют условию:
- •№2с). Точка:
- •№2d). Составить каноническое уравнение прямой, которая проходит через точку
- •№3. Фиксированная точкаM 0 ( 85 , 78 ,0)
- •4. Найти точку пересечения и угол между прямой
- •№4 . Косинус угла между прямой и плоскостью равен синусу угла между направляющим
- •Определить расстояния от точки
- •Расстояние d от точки M до прямой -длина высоты параллелограмма ,
- •1.Прослушать видео-лекцию 4 на тему: «Высшая математика. Аналитическая геометрия в пространстве».
- •Для нахождения уравнения прямой будем использовать уравнение прямой, проходящей через заданную точку перпендикулярно
- •информация о

Указать нормальный вектор прямой:
12x 5y |
24 0 -общее |
уравнение прямой.
Варианты ответов:
1. (5, 12);
2. (12, 5);
3. (12, -5).
Укажите номер правильного ответа.
97

|
x |
|
y |
|
1 |
|
a |
b |
|||
|
|
|
|||
Прямая отсекает от координатных осей |
|||||
отрезки a, b соответственно. (x, y) - |
|||||
координаты текущей |
точки |
||||
прямой . |
|
|
|
|
|
У |
|
|
|
|
|
b |
|
|
|
|
|
а
 Х
Х
98

M |
1 |
(x , y |
|
), M |
2 |
(x |
2 |
, y |
2 |
) |
–фиксированные |
|
||||||
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
||||||
точки; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
M (x, y) |
|
|
– текущая точка с переменными |
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||
координатами. |
|
|
|
|
|
|||||||||||||
|
x |
|
x1 |
|
|
|
|
y |
y1 |
|
|
|
|
|
|
|
|
|
|
x2 x1 |
|
y2 |
y1 |
|
- уравнение прямой |
|
|||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(x2 , y2 ) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M1 (x1 , y1 ), M 2 |
|
проходящей через две фиксированные |
|
|||||||||||||||||
точки |
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
||||
M2
M1
99

Составить уравнения прямой, проходящей через две фиксированные точкиM1 (3, 2) M 2 ( 5,1) и
, вычислить угловой коэффициент k этой прямой.
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Будем использовать уравнение |
|||||||||||||||||||||
|
|
x |
x1 |
|
y |
y1 |
|
|
x |
3 |
|
|
y 2 |
|
x 3 |
|
|
y 2 |
3x 8y 7 0 |
||||
|
|
x |
|
x |
|
|
|
5 3 |
1 2 |
8 |
|
||||||||||||
|
|
2 |
|
y |
2 |
y |
1 |
|
|
|
|
3 |
|
||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Выразим у в явном виде, т.е. приведем к |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( y |
kx b) |
|||
|
|
|
уравнению с угловым коэффициентом: |
||||||||||||||||||||
|
|
|
|
8y 3x 7 y |
3 |
x |
7 |
|
|
|
|
3 |
|
||||||||||
|
|
|
8 |
8 |
|
т.е.k 8 |
|||||||||||||||||
|
|
|
|
|
|
3 |
|
7 |
|
|
|
||||||||||||
|
|
Ответ: |
y 8 x |
8 |
|
- уравнение прямой с |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 8 |
|
|
|
|
-угловой |
||
|
|
|
угловым коэффициентом и |
|
|||||||||||||||||||
коэффициент. |
100 |
|




.,
.
|
|
Решение |
|
1а). Вектор нормали данной прямой |
|
|
x 3y 7 0 : |
. |
|
Так как искомая прямая параллельна |
|
|
данной, то вектор нормали данной |
|
|
может служить и |
|
вектором нормали |
|
искомой прямой |
106

,
Фиксированная точка на искомой прямой дана
Воспользуемся уравнением прямой,
проходящей через точку |
с |
нормальным вектором |
|
|
Для последней |
|
прямой вектор |
|
нормали |
|
имеет вид: |
107

,
Для полученной прямой: направляющий вектор (надо поменять местами координаты вектора нормали и у одной
сменить знак) |
, угловой |
|
коэффициент |
|
(надо записать |
|
уравнение в |
|
виде |
|
) |
108

,.
1b). Прямая задана в канонической форме и ее направляющий вектор
. Он может служить вектором нормали искомой прямой, так как прямые перпендикулярны. Таким образом, имея точку и вектор нормали
записываем уравнение прямой в виде:
109
