Комплексные числа

История развития комплексных чисел.

•Древнегреческие математики считали “настоящими” только натуральные числа. Постепенно складывалось представление о бесконечности множества натуральных чисел.

Следующим важным этапом в развитии понятия о числе было введение отрицательных чисел - это было сделано китайскими математиками за два века до н.э. Отрицательные числа применяли в III веке древнегреческий математик Диофант, знавший уже правила действия над ними, а в VII веке эти числа уже подробно изучили индийские ученые, которые сравнивали такие числа с долгом

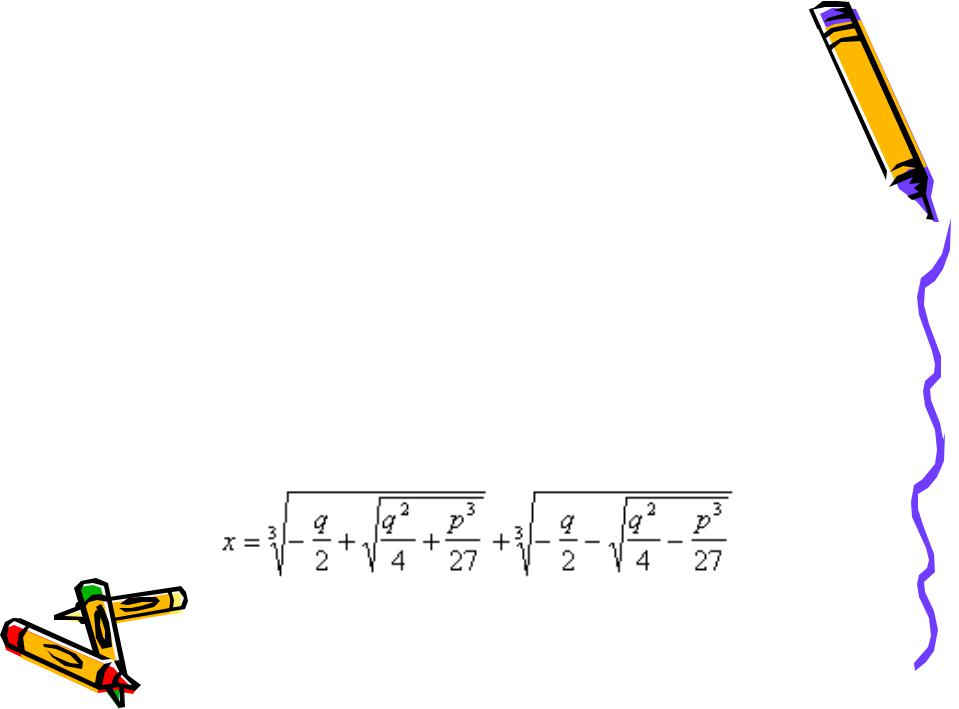
В XVI веке в связи с изучением кубических уравнений оказалось необходимым извлекать квадратные корни из отрицательных чисел. В формуле для решения кубических уравнений вида кубические и квадратные корни:

Постепенно развивалась техника операций над мнимыми числами. На рубеже XVII иXVIII веков была построена общая теория корней n-ых степеней сначала из отрицательных, а за тем из любых комплексных чисел, основанная на следующей формуле английского математика А. Муавра (1707):

Большой вклад в развитие теории функций комплексного переменного внесли русские и советские ученые Н. И. Мусхелишвили занимался ее применениями к упругости, М. В. Келдыш и М. А. Лаврентьев - к аэро- и гидродинамике, Н. Н. Богомолов и В. С. Владимиров - к проблемам квантовой теории поля.

Вид комплексного числа

Х²=-1

Х=i -корень уравнения

i- комплексное число, такое , что i²=-1

А + В· i

ЗАПИСЬ КОМПЛЕКСНОГО ЧИСЛА В ОБЩЕМ ВИДЕ

Комплексно сопряженные числа.

Z=А - В· i СОПРЯЖЕННОЕZ= А + В· i

(Z) = Z

Модуль комплексного числа

Z = A + B i= 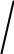А2 В2

Тригонометрическая форма комплексного числа

Z =r

φ- аргумент аргумент комплексного числа

Z=r cos φ + i Z sin φ = = r (cos φ+ i sin φ)

Для Z=0 аргумент не определяется

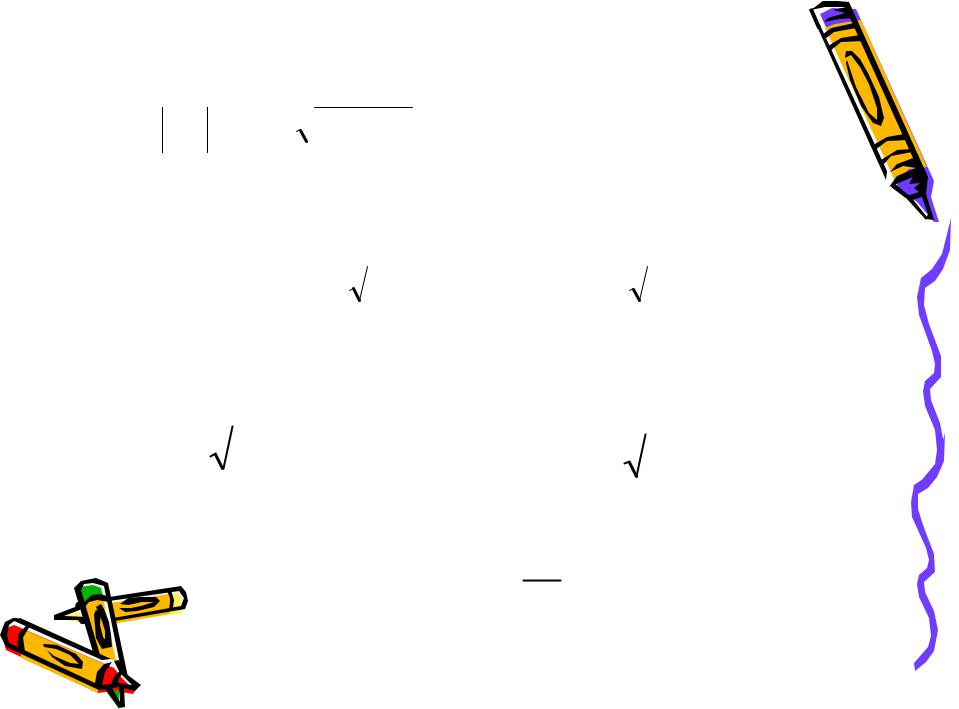
Т.к Z =r = А2 В2

tg BA