Сегодня: Thursday, July 4, 2019
Содержание лекции:
Лекция
Тема: ЭЛЕКТРОСТАТИКА
1.Закон Кулона
2.Принцип суперпозиции электрических полей
3.Электрические силовые линии
4.Электрические поля систем зарядов. Электрический диполь
5.Электрический потенциал
6.Связь между потенциалом и напряженностью
продолжение на следующем слайде…
7.Безвихревой характер электростатического поля
8.Поток вектора напряженности
9.Электростатическое поле равномерно заряженной плоскости и шаровой поверхности
9.1Электростатическое поле равномерно заряженной плоскости
9.2Электростатическое поле равномерно заряженной шаровой поверхности
10.Проводники в электрическом поле
10.1 Поле однородном проводнике 10.2. Поле во внутренней полости проводника
продолжение на следующем слайде…
10.3 Пробой при высоком напряжении
11.Диэлектрики в электрическом поле
11.1.Классификация диэлектриков, поляризуемость и дипольные моменты молекул
11.2.Вектор поляризации
11.3.Электреты. Пьезоэлектрики.
11.4.Сегнетоэлектрические кристаллы
12.ЭНЕРГИЯ СИСТЕМЫ ЗАРЯДОВ И ЭЛЕКТРИЧЕСКОГО ПОЛЯ
12.1.Электрическая емкость. Конденсаторы
12.2.Энергия взаимодействия электрических зарядов
|
1. Закон Кулона |
|
||
Электростатика |
изучает |
электрические |
поля |
|
неподвижных зарядов. |
|
|
|
|
Основной |
количественный закон электростатики |
|||
был открыт французским инженером Кулоном в 1785 г. |
||||
Закон Кулона утверждает, что между двумя |
||||
покоящимися точечными зарядами действует сила, |
||||
пропорциональная произведению зарядов и обратно |
||||
пропорциональная квадрату |
расстояния |
между |
||
ними. |
|
|
|
|
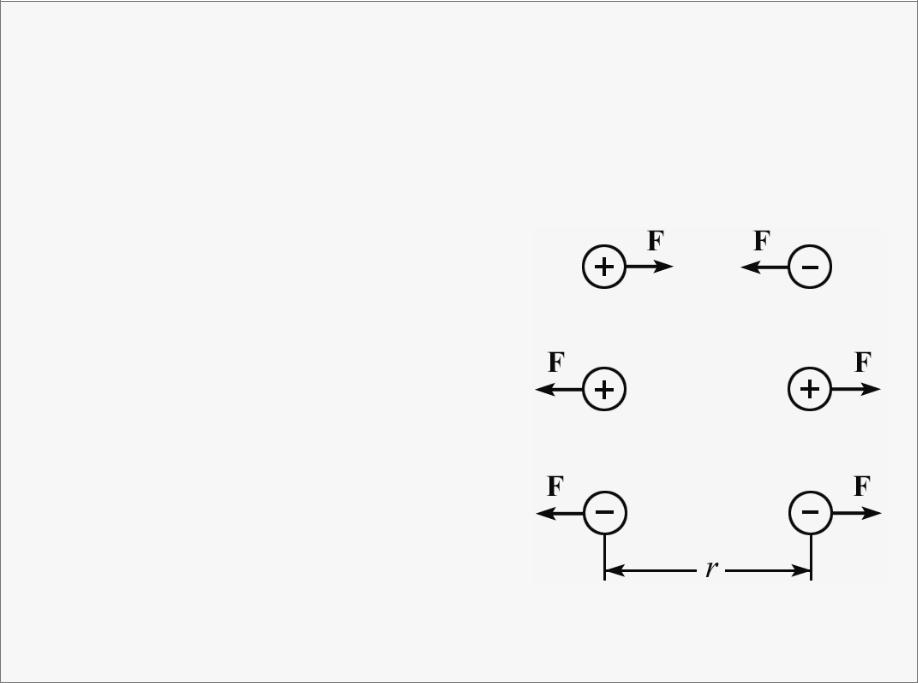
Сила направлена по прямой от одного заряда к другому.
Если знаки заряда разноимённые, то сила является силой притяжения, и силой отталкивания, если знаки зарядов одноимённые (рис. 1):
рис. 1
|
q1q2 |
|
|
|
|
|
|
r12 |
|
|
|
F1 k0 r2 |
|
F2 |
|||
r |
|
||||
12 |
12 |
|
|
||
Здесь F1 – сила, действующая на заряд q1;
F2 – сила, действующая на заряд q2; r12 – расстояние между зарядами q1 и q2; r12/r12 – единичный вектор, направленный от q2 к q1.
Множитель k0 определяется выбором системы единиц.
В СИ он записывается в виде k0 =
Величина 0 называется электрической постоянной и в СИ 0 =8.85 · 10-12 Ф/м или
k0=9 · 109Н·м2/Кл2
Величина - относительная диэлектрическая проницаемости среды, в которой находятся заряды.
Единицей заряда в СИ является кулон и обозначается Кл. Точечность зарядов в законе Кулона означает, что линейные размеры заряженных тел пренебрежимо малы по сравнению с расстоянием между ними.
Рассмотрим два шара из углерода. Пусть они имеют небольшой избыток электронов.
Найдем такое отношение числа электронов к числу протонов, чтобы электростатическое отталкивание в точности компенсировало силу гравитационного притяжения.
По условию F = F , т.е. |
k0 |
q1q2 |
G |
m1m2 |
E G |
r 2 |
r 2 |
(здесь q1 и q2 – заряды, а m1 и m2 – массы шаров), и можно записать
|
q |
|
q |
2 |
|
|
G |
||
|
1 |
|
|
|
|
|
|
||
|
|
|
k |
|
|||||
m |
m |
2 |
|
0 |
|||||
|
1 |
|
|
|
|
|
|
||
Если у обоих шаров отношения числа электронов к числу протонов одинаковы, то
|
|
q1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
G |
|
|
||||
Кроме того, q1 |
|
m |
|
|
k |
|
|
|
|
Кл |
|
|
|
|
|
|
|
|
|
||||
= (Ne – Np)e, |
e=1,6·10 |
-19 |
|||||||||
|
1 |
|
|
|
|
0 |
|
|
|
||
где Ne – число электронов, а Np – число протонов. Масса первого шара
m1 = Npmp + Nnmn + Neme,
где mp, mn и me – массы протона, нейтрона и электрона соответственно. Учитывая, что mp mn >> me и Np = Nn, получаем m1 = 2Npmp.
Тогда |
|
|
Ne N p e |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
q1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
G |
, |
|
||||||||||||||
|
|
m |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
2N |
p |
m |
p |
|
|
|
|
k |
0 |
|
|
|
|||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Ne N p |
|
|
|
2mp |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
G |
|
1,8 10 |
18 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
N p |
|
|
|
|
e |
|
|
|
|
k0 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
для компенсации |
|||||||||||
|
|
|
Следовательно, |
|
|
|||||||||||||||||||
гравитационного притяжения необходим лишь один дополнительный электрон на каждые 5 1017 протонов.