3.4.2. Вывод законов Ома и Джоуля –

Ленца в классической теории

электронной проводимости металлов

Исходя из того ,что электроны представляют в

металлах идеальный газ, попытаемся получить

закон Ома и выражение для электропроводности

металла.

Воспользуемся определением величины плотности

тока

j = enu.

Согласно

классической

теории

проводимости

электроны представляют точки, движущиеся под

действием внешнего поля Е.

В отсутствие поля средняя скорость

направленного движения электронов u равна нулю,

а средняя скорость хаотического движения v

определяется согласно молекулярно-кинетической

теории следующим выражением:

v

8мkT

105

m

с

e

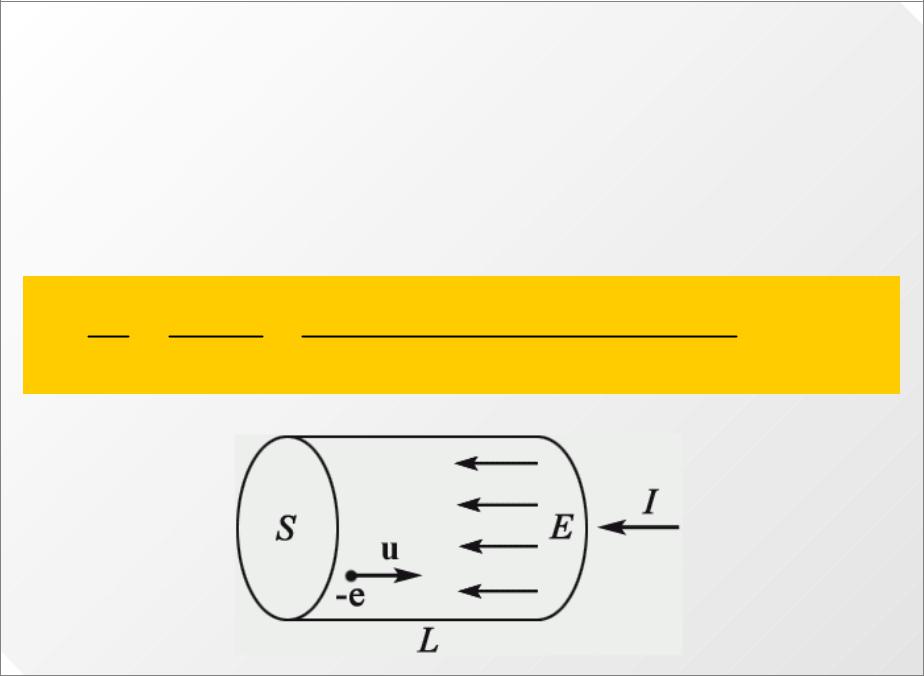
Под действием поля Е электроны приобретают

добавочную скорость u (рис. 3.4). Величина этой

скорости много меньше средней скорости

хаотического движения практически для всех

реально достижимых токов

u

j

I / S

107 А/м

10

3

м

en

en

19 Кл 8,5 1028 м 3

с

1,6 10

Здесь концентрация электронов подсчитана для

меди, n = NA /A

8,5 1028

м 3. Поэтому

столкновения электронов с дефектами, примесями и

ионами решетки связаны главным образом с

тепловым движением электронов и происходят в

среднем через промежуток времени

l

где l длин свободного v электрона.

За время электрон может приобрести среднюю

скорость направленного движения:

u = a = F

e E

,

m m

где a = F/m = eE/m ускорение, сообщаемое

электрону силой F = = eE.

Среднее значение скорости u

uср 0 u

1 eE

2

2 m

Подставив величину uср в выражение для

плотности тока получим

j

e2 nl

E

2mv

Плотность тока пропорциональна напряженности

поля, что соответствует закону Ома

j = E,

-величина электропроводности, равная

e2 nl

2mv

Металлы оказываются хорошими проводниками не

только электрического тока, но и тепла. Это связано

с тем, что переносчиками тепла и электричества в

металлах являются свободные электроны, а роль

ионов в передаче тепла пренебрежимо мала.

Коэффициент теплопроводности для металлов, как

ранее было показано, равен

= 1 nvC l,

V

где С

V

= (3/2)k теплоемкость при постоянном

3

объеме.

Разделив на , имеем (mv2 3kT) .

2

2

mv2

C

V

k

3

3

T

e2

e

что

закон Видемана

отношение коэффициента теплопроводности для

металлов к удельной электропроводности

пропорционально температуре и не зависит от рода

металла.

Этот закон был установлен в 1853 г.

экспериментально немецкими физиками Г.

Видеманом и Р. Францем. Теоретически закон был

обоснован в 1902 г. немецким. физиком

Друде

Совпадение результатов теории П. Друде с

экспериментом считалось долгое время веским

доказательством

справедливости

классической

теории

электропроводности

и

теплопроводности

металлов.

Но реально классическая теория дает неверные

значения для v2 и CV. Случайно эти ошибки

компенсируют друг друга, и фактически CVv2

получается верной. Последовательный вывод закона

Видемана – Франца может быть выполнен только в

рамках квантовой механики.

Классическая

теория

электропроводности

дает

правильное объяснение закону Джоуля Ленца, т.е.

тепловому действию тока.

Поскольку при каждом столкновении частицей

рассеивается дополнительно приобретенная энергия

mu2/2, а число таких столкновений в единице

объема равно n/ , то полное тепловыделение в

единице объема

w mu2 n

e2nl E2 = Е2

2

2mv