
лекции_1 / Лекция 4_Трение твердых тел
.pdf
Лекция 4. Трение твердых тел
Трение внешнее, механическое сопротивление, возникающее в плоскости касания двух соприкасающихся тел при их относительном перемещении. Сила сопротивления Fтр, направленная противоположно относительно перемещению данного тела, называется силой трения, действующей на это тело. Трение внешнее — диссипативный процесс, сопровождающийся выделением тепла, электризацией тел, их разрушением и т.д.
Различают Трение внешнее скольжения и качения. Трение скольжения — сила, возникающая при поступательном перемещении одного из контактирующих тел относительно другого и действующая на это тело в направлении, противоположном направлению скольжения. Трение качения — момент сил, возникающий при качении одного из двух контактирующих тел относительно другого, препятствующий качению.
Характеристика трения скольжения — коэффициент трения скольжения fc - безразмерная величина, равная отношению силы трения к нормальной нагрузке; характеристикой трения качения является коэффициент трения качения fk - величина, имеющая размерность длины, представляет собой отношение момента трения качения к нормальной нагрузке. Внешние условия (нагрузка, скорость, шероховатость, температура, смазка) влияют на величину Трения внешнего не меньше, чем природа трущихся тел, меняя его в несколько раз.
Fс = Fтр./mg (4.1) |
fк = Fтр.кач. R/mg (4.2) |
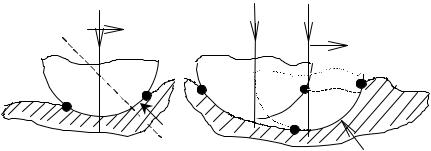
Механизм возникновения трения объясняет молекулярно-механическая теория трения, в разработку которой внесли большой вклад российские ученые (Б.В. Дерягин, И.В. Крагельский и др.) и зарубежные (Боуден, Тейбор, Томлинсон и др.). В соответствии с этой теорией трение имеет двойственную молекулярномеханическую природу. Силу трения Fтр можно представить как сумму молекулярной (адгезионной) Fа и механической (деформационной) Fσ составляющих:
Fтр = Fа + Fσ . |
(4.3) |
Молекулярная составляющая обусловлена сопротивлением разрыву молекулярных либо межатомных связей, которые возникают между контактирующими телами. Механизм этого процесса аналогичен разрушению кристаллической решетки при сдвиге. Рассеяние работы трения в теплоту связано с упругой деформацией кристаллических решеток. Работа внешней силы переходит в потенциальную энергию решеток. После
разрыва связи потенциальная энергия переходит в энергию колебаний атомов (тепло). |
|
|
||||||||||
|
Ni |
Ni |
Ni |
Механическая |
|
составляющая вызвана |
сопротивлением |
|||||
|
упругому и |
|
пластическому |
оттеснению выступов |
||||||||
|
Ti |
|
|
|
||||||||
|
|
Ti |
контактирующих тел, внедрившихся при движении в |
|||||||||
|
|
|
||||||||||
|
|
|
B1 |
контроповерхности (см. рис. 4.1). |
|
|
|
|||||
A |
B |
A |
B |
В зависимости от условий трения, а также от структуры |
||||||||
|
|
|
|
тел и межатомных взаимодействий, отдельные компоненты |
||||||||
|
|
R |
Ri |
в выражении |
|
(4.3) |
могут |
вырастать или |
уменьшаться. |
|||
|
|
A1 |
Различают |
4 |
вида |
трения: |
сухое, |
граничное, |
||||
|
а |
|
б |
|||||||||
|
|
гидродинамическое |
(жидкостное) |
и |
смешанное |
|||||||
Рис 4.1. Упругое и пластическое оттеснение |
||||||||||||
(одновременно имеются элементы сухого, граничного и |
||||||||||||
материала при скольжении |
|
гидродинамического трения). |
|
|
|
|||||||
В первом случае контактируют несмазываемые поверхности, покрытые окисными пленками и тончайшими слоями молекул газов и воды, адсорбированными из окружающей среды. В этом случае сила трения складывается из адгезионной и когезионной составляющих. Сухое и граничное трения сходны по своей

природе и имеют общие закономерности. Причиной служит то обстоятельство, что при граничном трении мономолекулярные слои смазки прочно связаны с твердой поверхностью, обладают твердообразными свойствами и как бы служат продолжением твердой фазы. Поэтому, как и при сухом трении, фактически имеет место контакт двух твердых поверхностей. Отличие проявляется в разных значениях коэффициента трения.
Во втором случае, помимо перечисленных пленок, присутствуют молекулы смазочных материалов в виде тонкого слоя толщиной в несколько молекул, которые прочно связаны с поверхностью. Характерным в этом случае является снижение как той, так и другой составляющей.
В третьем случае слой жидкой смазки полностью разделяет сопряженные поверхности. Адгезионная составляющая уменьшается до нуля.
Многочисленные исследования показали, что для металлов деформационная составляющая коэффициента трения примерно в 100 раз меньше, чем адгезионная. Поэтому коэффициент трения в первом приближении равен адгезионной составляющей. Несколько иначе дело обстоит для пластмасс и резин. В последнем случае различие снижается более чем на порядок, и, если резина скользит по грубо обработанной поверхности, деформационной составляющей пренебрегать не следует.
|
|
|
|
|
|
N |
1 |
|
|
Для измерения силы трения применяют различные трибометры. |
|
|
|
|
|
|
|
|
На них изучают трение образцов в виде дисков, контактирующих |
||
|
|
|
|
|
|
F |
|
3 |
|
торцами; цилиндров, контактирующих по образующей, и т.д. |
|
|
|
|
|
|
|
|
Наиболее простым и часто используемым является трибометр, |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
схема которого изображена на рис. 4.2. Образец 1 прикрепляется к |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пружинному динамометру 3 и прижимается к контртелу 2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
приводимому в движени е. |
|
V |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Динамометр измеряет силу трения. Прибор позволяет исследовать |
|
|
|
|
|
|
|
2 |
|
|
влияние на трение шероховатости поверхностей, материалов пары |
|
|
|
|
|
|
|
|
|
трения, нормальной нагрузки, скорости скольжения, температуры, |
|
смазки и многих других факторов.
Рис. 4.2. Схема трибометра
Определение сил и коэффициентов внешнего трения. При упругих деформациях в зонах касания взаимодействие твердых тел может осуществляться при ненасыщенном и насыщенном контакте.
При упругом ненасыщенном контакте расстояния между отдельными зонами контактирования достаточно велики, так что влиянием зон друг на друга можно пренебречь. Общая сила трения при скольжении абсолютно жесткого тела, обладающего шероховатой поверхностью, относительно более мягкого тела, обладающего абсолютно ровной поверхностью, будет равна
nr |
|
|
F тр = ∫F i |
dnr , |
(4.4) |
0 |
|
|
где Fi – сила трения, возникающая на единичной произвольной микронеровности; nr – число микронеровностей, имеющих одинаковое внедрение.
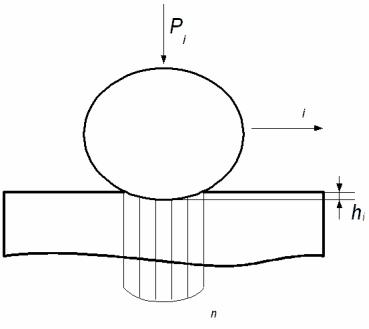
Для определения силы Fi рассмотрим процессы, происходящие в зоне контакта единичной микронеровности (рис. 4.3). Деформационная составляющая силы трения возникает вследствие несовершенной упругости материала деформируемых слоев. Она обусловлена гистерезисными потерями. В соответствии с исследованиями английского ученого Д. Тейбора
деформационная составляющая силы трения равна
Fiдеф = |
0,25α |
h2 E |
, |
|
||
|
|
гист i |
(4.5) |
|||
1 |
− μ2 |
|||||
|
|
|
||||
где E – модуль упругости деформируемого материала; μ - коэффициент Пуассона этого материала; αгист – коэффициент гистерезисных потерь материала в условиях сложного напряженного состояния.
Рис. 4.3. распределение напряжений при упругих деформациях в зоне контакта шара с плоской поверхностью деформируемого тела
Молекулярная составляющая силы трения обусловлена межатомным и межмолекулярным взаимодействием и равна
Fiмол = (τ0 + βPri)πRhi |
(4.6) |
Тогда общую силу трения, возникающую при скольжении произвольной микронеровности, можно выразить следующим образом
Fi = |
0,25α |
|
h2 E |
+ (τ0 |
+ βPri)πRhi |
(4.7) |
|
гист |
i |
||||
|
|
|
|
|
||
|
1 − μ2 |
|
|
|
||
Сила трения Fтр вычисляется из выражения (4.4), в котором все i-е параметры определяются через известные величины. Если определить
нормальную нагрузку P в зависимости от сближения, то можно вычислить коэффициент трения в зависимости от сближения f =
Fтр/P. Расчеты показывают, что при увеличении сближения между поверхностями твердых тел молекулярная составляющая
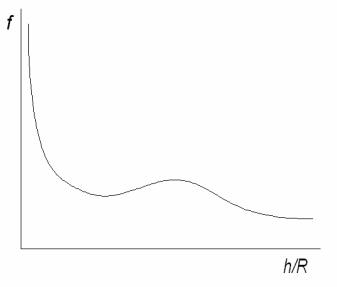
коэффициента трения (содержащая фрикционные параметры τ0 и β) уменьшается, а деформационная возрастает. Зависимость коэффициента трения от параметра h/R показана на рис. 4.4.
Рис. 4.4.Зависимость коэффициента трения от сближения
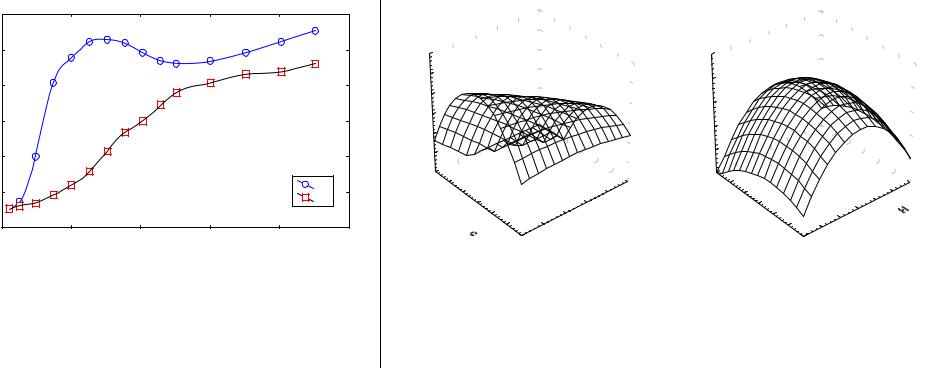
Экспериментальные результаты. Поведение материала при трении определяется глубиной распространения пластической деформации внутрь образца. С ростом нормального давления на пятнах факти-ческого контакта развиваются сначала упругие, а затем пластические деформации. Некоторое формоизменение, связанное с ползучестью материала, происходит и после, в условиях действия постоянной нагрузки. Окончательное равновесие устанавливается после того, как площадь фактического контакта оказывается достаточной для обеспе-чения необходимой несущей способности. Таким образом, после приработки поверхности устанавливается стационарный режим трения, при котором износ поверхности находится в равновесии с ростом новых деформированных слоев. На рис. 4.5 и 4.6 приведены зависимости коэффициента трения от давления в установившемся режиме граничной смазки при скольжении образцов из стали 36НХТЮ в закаленном и состаренном состояниях по закаленной стали 45. Аустенитная сталь 36НХТЮ
отличается высокой коррозионной стойкостью, |
поэтому при трении оксидные слои не образуются, |
что |
||||||||||
|
|
|
|
|
|
|
|
обусловливает схватывание уже при незна- |
||||
0.17 |
|
|
|
|
|
|
|
чительном нагружении. Более высокая |
||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
несущая |
способность состаренного сплава |
|||
|
|
а |
|
|
|
|
|
|||||
0.15 |
|
б |
|
|
|
|
|
объясняется высоким пределом текучести и |
||||
|
|
|
|
|
|
|
|
твердостью. |
|
|
|
|
0.13 |
|
|
|
|
|
|
|
Следует заметить, что при различных |
||||
k |
|
|
|
|
|
|
|
условиях |
экспериментальные зависимости |
|||
0.11 |
|
|
|
|
|
|
|
коэффициента трения от нагрузки, скорости и |
||||
|
|
|
|
|
|
|
|
температуры могут быть возрастающими, |
||||
0.09 |
|
|
|
|
|
|
|
убывающими, |
неизменными |
и |
с |
|
|
|
|
|
|
|
|
|
экстренумами. Параметры трения - износ и |
||||
0.07 0 |
0.1 |
0.2 |
0.3 |
|
|
коэффициент трения зависят от структуры |
||||||
0.4 |
||||||||||||
|
|
|
|
P, МПа |
|
|
|
поверхностного слоя и кинетики его |
||||
Рис. 4.5. Зависимость коэффициента трения (k) от давления |
деградации, которые, в свою очередь, |
|||||||||||
для сплава 36НХТЮ закаленного от 9700С (а) и состаренного |
определяются внешними условиями. Поэтому |
|||||||||||
после закалки при 7500С в течение 1 часа (б). |
|
|
|
и существует |
необходимость |
изучения |
||||||
структуры и триботехнических свойств материалов в каждом конкретном случае, применительно к тому или иному узлу трения.
|
0.6 |
|
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
k |
0.3 |
|
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
|
0.1 |
|
|
|
|
|
- 1 |
|
|
|
|
|
|
- 2 |
|
|
|
|
|
|
|
|
|
|
0 |
0 |
2 |
4 |
6 |
8 |
10 |
|
|
|
|
|
P, МПа |
|
|
Рис. 4.6. Зависимость коэффициента трения
(k) от давления для сплава 36НХТЮ закаленного от 9700С (1) и состаренного после закалки при 7500С в течение 1 часа (2)
а |
б |
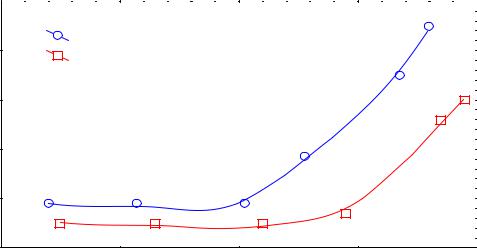
Рис.4.7. Зависимость коэффициента трения образца из стали 36НХТЮ (а) и меди (б) от скорости скольжения и нагрузки
На рис. 4.7 показаны поверхности, образованные значениями коэффициента трения меди и сплава 36НХТЮ, в зависимости от скорости скольжения и нагрузки. Коэффициент трения меди изменяется по кривой с максимумом в зависимости от нагрузки при всех скоростях. Для сплава 36НХТЮ коэффициент трения при малых скоростях практически не зависит от прикладываемого усилия. Возрастание нагрузки при больших скоростях приводит к падению коэффициента трения. Это свидетельствует о том, что вклад в силу трения, обусловленный пластическим течением поверхностного слоя, уменьшается. Такое возможно при уменьшении
вязкости материала, связанном с увеличением возбуждения при трении. По-видимому, при этом имеет значение процесс фрагментации поверхностных слоев, который приводит к возрастанию подвижности составляющих структуру элементов.
Р,кН
|
|
|
|
а |
|
22 |
|
|
220 |
|
18 |
P (Т) |
|
180 |
|
|
M (Т) |
|
|
|
14 |
|
|
140 |
Р,кН |
10 |
|
|
100 |
|
|
|
М,Нм |
|
|
6 |
|
|
60 |
|
2 |
|
|
20 |
|
-2 |
400 |
1200 |
-20 |
|
0 |
2000 |
22 |
|
220 |
|
18 |
P (T) |
180 |
|
14 |
M (T) |
140 |
|
|
|
||
10 |
|
100 |
Нм |
|
|
|
М, |
6 |
|
60 |
|
2 |
|
20 |
|
-2 |
|
-20 |
|
|
0 |
400 |
800 |
1200 |
1600 |
б |
|
|
|
|
Т,с |
|
|
|
35 |
|
|
|
|
220 |
|
30 |
P (T) |
|
|
|
180 |
|
|
|
|
|
||
|
25 |
M (T) |
|
|
|
140 |
|
20 |
|
|
|
|
|
Р,кН |
|
|
|
|
|
|
15 |
|
|
|
|
100 |
|
10 |
|
|
|
|
М,Нм |
|
|
|
|
|
|
60 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
20 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
-5 |
1000 |
2000 |
3000 |
4000 |
-20 |
|
0 |
5000 |
Т,с |
в |
T,c |
г |
|
|
|
Рис. 4.8. Зависимость момента силы трения композиционного материал TiC-NiCr (а) от нагрузки в паре с различными сплавами (б - TiC-NiCr; в – 3В16К; г – композиция на основе бронзы КАМ)
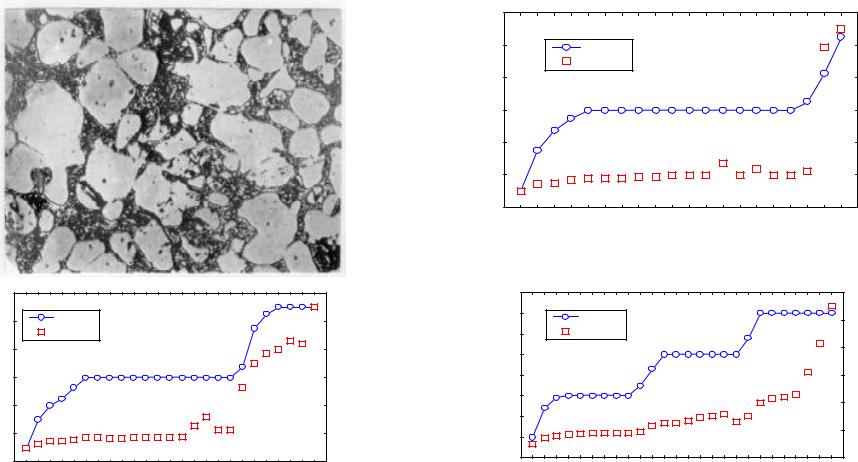
Анализ параметров трения (рис. 4.8) показывает , что большую роль в процессе контактирования двух материалов при их относительном скольжении играет тепло, выделяющееся на поверхности и в приповерхностном слое.
Действительно, примером влияния контактной температуры на процесс трения может служить поведение композиционного материала TiC-NiCr при трении в паре с материалами, среди которых были КМ TiC-NiCr, стеллит и композиция “твердый сплав - бронза”, различающиеся теплопроводностью. В данных испытаниях, когда сопряжение было в виде торцевого уплотнения, отвод тепла из зоны трения может осуществляться в основном за счет теплопроводности контактирующих материалов. Поскольку теплопроводность КМ TiCNiCr и стеллита (3В16К) значительно меньше, чем у композиции КАМ, разработанной для высоконагруженных узлов трения, характер трения должен различаться. Действительно, из рис. 4.8,б видно, что трение пары одинаковых КМ TiC-NiCr становиться нестабильным уже после нескольких минут работы при нагрузке 1 т. Повышение нагрузки до 2 т сопровождается скачками момента трения, что свидетельствует
|
|
о заклинивании сопряжения. В паре со стеллитом КМ TiC- |
Температура |
|
NiCr также ведет себя нестабильно (рис.4.8,в), а при нагрузке |
|
2 т испытания были прекращены из-за очень высокого |
|
|
|
|
|
|
момента трения. Иное поведение наблюдается, когда |
|
|
контртелом служил материал КАМ. Критическое значение |
|
|
момента трения наблюдалось лишь при нагрузке 3 т после |
|
|
нескольких минут работы (рис. 4.8,г). По-видимому, |
|
|
работоспособность материала сохраняется до тех пор, пока |
|
|
температура в зоне трения (рис. 4.9) не достигнет значений, |
|
|
при которых происходит схватывание. |
|
|
|
Рис. 4.9. Схематическое изображение распределения температуры в поверхностном слое в случае пластической деформации при трении
