Лекция 2. Деформации
•Деформацию тела под действием внешних сил связывают с изменением формы и размеров тела.
•Если устранение причины деформации (разгрузка) приводит к исчезновению деформации, то деформацию называют упругой или обратимой.
•Если устранение причины деформации не приводит к полному исчезновению деформации, то оставшуюся часть деформации называют необратимой или пластической.
•Различают абсолютную деформацию и относительную
деформацию
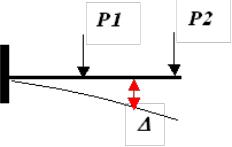
Абсолютная деформация
•Абсолютная деформация характеризует интегральную реакцию тела на внешнее воздействие. Примеры абсолютной деформации – прогиб балки, удлинение стержня, угол закручивания вала.
•Мерой абсолютной деформации является перемещение одной или нескольких точек тела из начального положения в конечное.
Относительная деформация
•Чтобы получить характеристику интенсивности изменения формы и размеров тела вводят понятие
относительной деформации.
•Относительная деформация характеризует реакцию рассматриваемой точки (области) тела на внешнее воздействие.
•Различают линейную и угловую относительную деформацию
•Под точкой тела в сопротивлении материалов понимают объем некоторого элементарного параллелепипед.
Относительная линейная деформация
Под действием сил произойдет изменение размеров граней параллелепипеда y 
|
dy |
|
|
|
dy |
dx |
dx |
x |
Относительнаялиейнаядеформация–эттношение
удлиенияdxотрезакегончальнойдлинеdx.
dx
x dx
Аналогично
d dz
y d z dz
Относительная угловая деформация
Предположим, что элемент изменил также форму – прямоугольный параллелепипед стал косоугольным.
Опрделимугловуюдеформациюкамеруизменияпр xy
угла,вданомслучаеугламеждуосямиxиy:
dx |
dx |
||
xy a tan |
|
|
dy |
|
dy |
|
|
Аналогично dy |
|
|
dz |
|
|
||
yzdz |
zxdx |
||
Закон Гука. Модули упругости
З а к о н Г у к а о т р а ж а е т эк с п е р и м е н т а л ь н о у с т а н о в л е н н у ю л и н е й н у ю за ви с и м о с т ь м е ж д у о т н о с и т е л ь н ы м и д е ф о р м а ц и я м и и н а п р я ж е н и я м и .
Д л я н о р м ал ь н ы х н ап р я ж е н и й
|
x |
E x , |
гд е |
Е – м о д у л ь у п р у го сти п е р в о го р о д а (м о д у л ь Ю н г а ). |
|
Д л я к а са те л ь н ы х н ап р я ж ен и й |
||
|
xy |
G xy , |
гд е |
G – м о д у л ь у п р у го с ти в то р о го р о д а (м о д у л ь с д в и г а ). |
|
Коэффициент Пуассона
КоэффициентПуассона устанавливает связь между продольными x и поперечными ( у и y)
относительными деформациями
y zx x
Растяжение – сжатие прямого стержня
Растяжение (сжатие) – деформация стержня под действием сил, направление действия которых совпадает с осью стержня, проходящей по центрам тяжести всех нормальных сечений стержня.
Напряжения при растяжении
dN |
X |
|
X |
dF |
N |
X |
|
dF |
X |
F |
|||
|
|
|
|
|
X |
|
|
|
|
||||
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
X |
N X |
|
|
X x |
NX (x) |
|
|||||
|
|
|
|
|
|||||||||
|
|
F |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
F(x) |
|
|
||
Деформации и перемещения при растяжении
|
|
|
dx |
|
|
X |
|
N X |
|
dx X dx |
|
N X dx |
||||||
X |
|
|
|
|
|
|
|
|
|
|
||||||||
|
dx |
E |
EF |
|
|
EF |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
NX x dx |
|
|||||
|
x |
x |
|
dx x |
NX dx |
|
|
|
x x |
x dx x |
|
|
|
|||||
|
|
|
|
|
|
|||||||||||||
|
N |
|
X |
|
|
|
EF |
|
|
N |
X |
|
|
|
|
|||
|
|
|
0 |
|
|
0 |
|
|
|
|
|
0 |
0 |
E x F x |
|
|
||
Температурноеудлинениестержняравно
x
x Txd,
T
0
где -коэфициентлинейноготемпературногорасширенияиTx - законизменениятемпературыподлинестержня.
U x |
N |
x |
x x |
|
x dx x |
T x dx |
U |
N X L |
TL |
|
|||||||||
|
T |
X |
|
|
EF |
||||
|
|
|
0 |
|
0 |
|
|
||