4.2. Статические и динамические нагрузки приводов механизмов непрерывного действия

При движении конвейера приводной двигатель должен преодолевать статическую нагрузку, обусловленную силами трения во всех движущихся элементах, а также составляющую силы тяжести транспортируемого груза на наклонных участках конвейера. Силы трения возникают в подшипниках вращающих элементов, в местах контакта роликов и катков с опорой, в тяговом элементе при его изгибах и вследствие значительной протяженности конвейера и большого количества движущихся элементов составляют значительную часть суммарной статической нагрузки, а для горизонтальных конвейеров определяют всю статическую нагрузку привода.

Силы сопротивления движению конвейера можно разделить на две категории: силы, не зависящие от натяжения тягового элемента, и силы, зависящие от натяжения. Первые возникают на прямолинейных горизонтальных и наклонных участках и распределены по участку равномерно (рис. 56, а, б). Вторые возникают на участках изгиба тягового элемента и сосредоточены в рамках дуги этого участка (рис. 57 а – в).

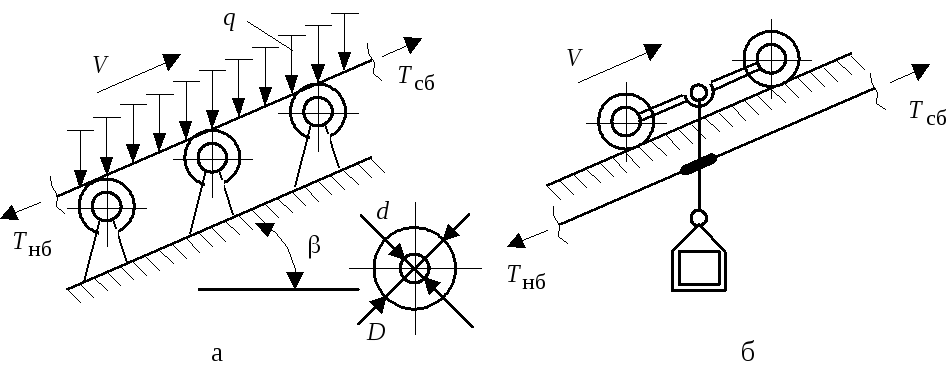
Рис. 56. Прямолинейные участки ленточного (а), цепного и канатного (б) конвейеров (– натяжение в набегающей и сбегающей точках участка)

В соответствии с рис. 56 сила сопротивления движению определяется по выражению

, (4.1)

где:

q – весовая нагрузка на 1 м пути;

l – длина участка;

–результирующий коэффициент сопротивления движению на прямолинейном участке;

;

–коэффициент трения в подшипниках;

f – коэффициент трения качения роликов и катков.

Первое слагаемое в выражении (4.1) обусловлено потерями трения, а второе – составляющей веса перемещаемого по наклонному участку конвейера груза. В расчетах следует применять при движении на подъем ипри движении на спуск. В приближенных расчетах можно пользоваться значениямиприведенными в табл. 4.1.

Рис. 57. Участки изгиба тягового элемента на блоке (а), шине (б), и батарее роликов (в) (- угол обхвата)

Таблица 4.1.

Значение результирующего коэффициента сопротивления движению для конвейеров с подвижными опорами на подшипниках качения

Тип конвейера
Канатная дорога
Ленточные и цепные конвейеры

На участках изгиба (рис. 57, а – в) сила сопротивления движению состоит из двух слагаемых: силы от изгиба тягового элемента, пропорциональной натяжению в набегающей точке участка, и силы трения в подшипниках блоков или роликов, пропорциональной равнодействующей силеN на участке.

, (4.2)

где – коэффициент сопротивления от изгиба тягового элемента.

В конвейерных установках обычно выполняются условия:

Поэтому при определении равнодействующей силе N можно пренебречь весом блока G и принять, что натяжение в набегающей и сбегающей точках участка равны. Тогда выражение (4.2) приводится к виду

где – результирующий коэффициент сопротивления на участке изгиба.

В приближенных расчетах можно пользоваться значениями приведенными в табл. 4.2.

Таблица 4.2.

Значение результирующего коэффициента сопротивления движению на участках изгиба трассы конвейера

Вид участка изгиба трассы	№ рис.	Угол обхвата
Звездочка с цепью и шкив с канатом	57, а
Барабан с лентой	57, а
Цепь с катками по шине	57, б
Лента на роликовой батарее	57, б
Цепь на роликовой батарее	57, в

Сила сопротивления вызывает увеличение натяжения тягового элемента на каждом участке.

Для прямолинейного участка

. (4.3)

Для участка изгиба

, (4.4)

где – коэффициент увеличения натяжения на данном участке.

В общем случае конвейер может состоять из многих участков (рис. 58).

Рис. 58. Общая схема конвейерной линии

Так как прямолинейные участки отделяются друг от друга участками изгиба, то по всей замкнутой конвейерной линии имеется одинаковое число n прямолинейных и криволинейных участков.

Тогда результирующая сила сопротивления движению определяется как сумма сил всех участков

(4.5)

Так как силу должен преодолеть приводной элемент, то очевидно, что при установившемся движении разность натяжений на нем уравновешивается силой сопротивления

. (4.6)

Второе слагаемое в уравнении (4.5) зависит от натяжения, поэтому для расчета необходимо последовательно определять натяжение на участках. При этом должно быть известно заранее натяжение в какой-либо точке тягового органа, которая и принимается за исходную в расчете. Предположим, что известно месторасположение приводного элемента и натяжение на его сбегающей точке. Следуя от этой точки по направлению тягового элемента, пронумеруем все прямолинейные участки П и участки изгиба И (см. рис. 58). В соответствии с (4.5) и рис. 58, определив последовательно натяжение на входе участков изгиба, выразимна приводном элементе через исходно принятое значение

Полученное выражение для можно преобразовать к виду

, (4.7)

причем результирующий коэффициент увеличения натяжения от всех участков изгиба (без приводного элемента) и результирующее усилие сопротивленияна прямолинейных участках трассы могут быть описаны выражениями

На основании уравнений (4.4) и (4.5) получим

. (4.8)

Выражение (4.8) позволяет при известном значении определить результирующую силу сопротивления движению без расчетов натяжений на всех промежуточных участках.

Из выражений (4.7) и (4.8) следует, что чем меньше , тем меньше будут как максимальное натяжение цепи, так и. Однако по условиям работы конвейера регламентированы максимально допустимый провис тягового органа любого вида (цепь, канат, лента) и максимально возможное отношениедля тягового органа, фрикционно соединенного с приводным элементом (лента, канат). Для выполнения этих условий в тяговом органе с помощью натяжного устройства должно быть обеспечено определенное предварительное натяжение.

Для цепных конвейеров задача определения решается следующим образом:

1. При известном расположении приводной станции предположительно определяется точка конвейерной линии с минимальным натяжением. Этой точкой может оказаться точка сбегания на приводном элементе или самая низшая точка по ходу конвейера относительно приводного элемента при условии, что ;

2. Точке с минимальным натяжением приписывается заданное конструкторами, по условиям допустимого провеса значение предварительного натяжения .

3. По известному с помощью выражений (4.3) и (4.4) определяется значение.

4. Если , то точка минимального натяжения выбрана правильно. Приминимальное натяжение, равное, следует приписать точке сбегания на приводном элементе.

5. По найденному значению по выражениям (4.7) и (4.8) рассчитываются значенияи.

Для ленточных и канатных конвейеров на инакладывается условие Эйлера, исключающее пробуксовывание тягового элемента относительно приводного

, (4.9)

где

–угол обхвата приводного элемента;

–коэффициент трения между тяговым и приводным элементами (см. табл. 4.3).

Таблица 4.3.

Коэффициент трения между тяговым и приводным элементами

Тип конвейера
Ленточный
Канатная дорога

Соотношение (4.9) совместно с (4.7) дает условие для выбора значения

. (4.10)

Выбираемое по (4.10) значение должно иметь определенный запас по превышению правой части, так как в процессе эксплуатации необходимо учитывать изменение коэффициента трения, а также динамические нагрузки при пуске конвейера.

Задача по определению статической нагрузки приводной станции конвейера оказывается комплексной. В процессе расчета силы сопротивления движению одновременно определяется минимально необходимое натяжение тягового элемента и точка его месторасположения на конвейерной линии. Эта точка оказывается оптимальным местом расположения натяжного устройства, так как при этом от него потребуется минимальное усилие.

Динамические нагрузки привода конвейера возникают в процессе пуска и определятся движущимися массами собственно конвейера и его приводной станции

,

где

–динамическая сила на обводе приводного элемента с радиусом ;

–движущаяся масса одного прямолинейного участка совместно с массой предшествующего участка изгиба;

–моменты инерции двигателя и приводного элемента;

–передаточное отношение редуктора приводной станции;

–ускорение конвейера при пуске.

Для тяжелых конвейеров динамическое усилие за счет большой поступательно движущейся массы может оказаться значительным и существенно превосходить силу статического сопротивления. При этом слагаемое, вызванное поступательно движущимися массами, может составлять 90% и более результирующего динамического усилия. Пуски конвейера с длительным режимом работы осуществляются редко и, как правило, вхолостую. Тем не менее, высокий уровень динамических нагрузок и возможность пуска под нагрузкой после аварийной остановки вынуждают учитывать в расчетах силу . Так как при пуске результирующее усилие приводавозрастает, то увеличивается максимальное натяжение в тяговом элементе за счет дополнительного приращения натяжения на каждом участке

(4.11)

С учетом (4.11) результирующее натяжение на набегающем крае приводного элемента по сравнению с установившемся режимом (4.7) повысится

, (4.12)

причем расчетная суммарная масса определяется выражением

.

Следовательно, условие (4.10) выбора значения для ленточных и канатных конвейеров должно быть скорректировано с учетом (4.12)

.

Таким образом, динамические нагрузки при пуске конвейера могут существенно повысить как максимальное натяжение в тяговом элементе, так и необходимое значение предварительного натяжения . Чтобы исключить высокий уровеньв установившемся режиме для крупных конвейерных установок применяют вспомогательное натяжное устройство, которое создает дополнительное натяжение только на период пуска конвейера.