ЛЕКЦИЯ 4 Задачи теплопроводности в различных системах координат.

Цилиндрическая система координат

Уравнения теплопроводности для тел канонической формы

Стационарные задачи теплопроводности в различных системах координат

Электрическая аналогия

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Политехнический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Князева_лк / лекция_4.ppt

Скачиваний:

Добавлен:

30.05.2015

Размер:

2.63 Mб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

Декартова система координат

T T x, y, z,t ,

(1)

(2)

(3)

В практике часто встречаются такие условия, которые приводят к необходимости записи уравнения теплопроводности в иной форме, более удобной для представления решения и его физической трактовки.

Зависимость вида уравнения от используемой системы координат можно исключить, используя операторную запись

1 T	q	2	2	2
a t T	V
a t T		x2	y 2	z2

a c

c	T div	gradT	q	или	c	T T q		(4)
	t		V	или		t	V	(4)
	t					t

Слагаемые, выражающие тепловыделение и аккумулирование энергии, инвариантны относительно системы координат (т.е., неизменны); но слагаемые, выражающие результирующий кондуктивный тепловой поток, зависят от геометрии и, следовательно, от системы координат.

r, , z

z	r	dr	c	T	div q q		(5)
dz				t
					q T
		r , , z
z
		y	x r cos			y r sin	(6)

x
		d
		d
	y

dy	dr
dy	d
dx	x
z

1 T	1				T	q
a t		r		r		V

			r		r

1 2

r r

r 2 2

T ;q

1 T ;q

1 T

1 2T

a t

r2 2

r r

	(9)
	(9)	a c
		a c
		T Ts

(7)

(8)

Сферическая система координат

r, ,

1 T

div q q

a t

r , ,

q T

sin

r 2 r

2 sin

2 sin 2

; q

1 T

; q

(10)

r sin

1 T

2 T

sin

(11)

a t

r2 sin 2

r2 sin

1 T

(12)

r2 r

x r sin cos

y r sin sin

z r cos

Запись уравнений в различных системах координат особенно удобна, когда нужно найти распределение температуры в телах канонической формы – в цилиндре или шаре. В этих случаях уравнения существенно упрощаются при задании особых условий, когда поле температуры зависит только от одной координаты.

параллелепипед

	1 T	2T qV
пластина	a t	x2
пластина

	1 T	1				T	q
цилиндр	a t		r		r		V

				r		r

	1 T	1			2	T	q
сфера				r			V
	a t	r2
			r			r

q e

T T s

1 T

n T

Три последних

a t

(13)

уравнения вместе:

rn r

n 0 плоскость

n 1 цилиндр

n 2

сфера

T T0

T* T0

На доске

(14)

qV r*2

пространственныйХарактерный

Fo at*

;

T* T0

масштаб задачи

T T

* 1:

r 2

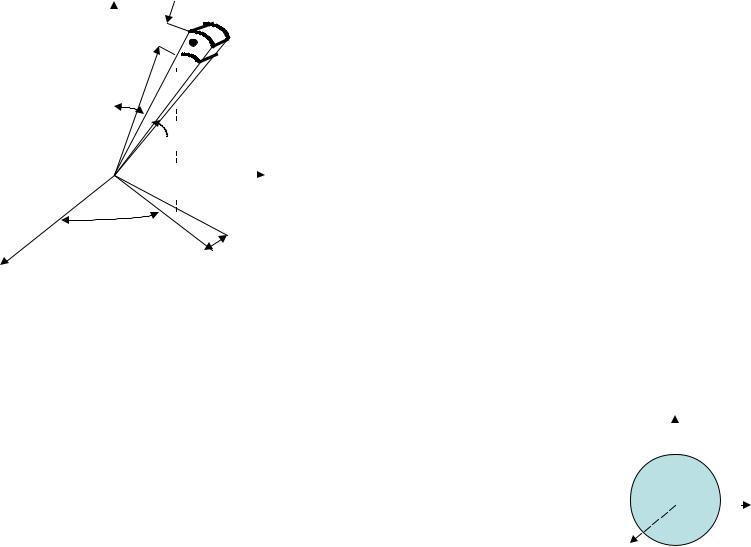
Цилиндрическая стенка: стационарный процесс теплопроводности в

цилиндрической стенке (трубе) с внутренним радиусом

r1 :

d1 2r1

1 T

1 2T

d 2T

1 dT

(15)

a t

r2 2

dr2

r dr

Te1

1 T1 T2

Te2

dT	u	du	1 u 0	lnu ln r lnC1	(16)
dr		dr	r
T C1 ln r C2			(17)
T C1 ln r C2			(17)	Удельный тепловой поток не
		dT	C1 (18)	постоянен по толщине и убывает по
		dT	C1 (18)	направлению к внешней поверхности
	q dr			направлению к внешней поверхности
			r
			r

В стационарных условиях постоянным должен быть полный тепловой поток проходящий через

участок цилиндрической трубы длиной		l и равный
	Q q F q 2 rl		(19)
	Удельный тепловой поток	Площадь поверхности
	убывает с радиусом	увеличивается с радиусом

!!!	Температура по толщине трубы изменяется нелинейно даже при постоянном
!!!	коэффициенте теплопроводности

Постоянные интегрирования могут быть найдены из граничных условий.

Граничные условия первого рода		r r1 : T T1; r r2 : T T2
Система линейных		T1 C1 ln r1 C2 ,

уравнений		T2 C1 ln r2 C2 ,
T	T1 ln r2 r T2 ln r r1		;	(20)

		ln r2 r1

q dTdr Cr1

Погонный тепловой	qп Q	2	T const,	T T1 T2	(22)
		ln r2 r1
поток	l

Граничные условия третьего рода

(температуры стенок – неизвестны)

Можем поступить аналогично:

T C1 ln r C2

r r : T

T T

; r r :

Поступим иначе:

Конвективный тепловой поток на единицу длины

трубы должен равняться погонному тепловому потоку

вследствие теплопроводности:

qп 1 Te1 T1 2 r1

qп Kc Te1 Te2

(24)

(23)

T T

ln r

1 2

Вт/(М·К) (25)

ln 2

2 r

1 1

2 2

Коэффициент теплопередачи для	R		1			1					1		r		1				(26)
Коэффициент теплопередачи для	R											ln 2							(26)
	c		K	c		2 r				2			r		2	r
				c			1 1						1			2 2
Полное термическое		от											плоская стенка						1
сопротивление трубы		от							1		L		1			1	L	1
сопротивление трубы	К для					R								K

																			2
																			2
	плоской стенки!																		Вт/(М ·К)
	плоской стенки!							1					2			1		2	Вт/(М ·К)
								1					2			1		2
Из системы уравнений (23) мы можем найти					T T1 ln r2							r T2 ln r r1 ;						Можно
и температуры стенок и подставить в (20)											ln r2			r1				на доске

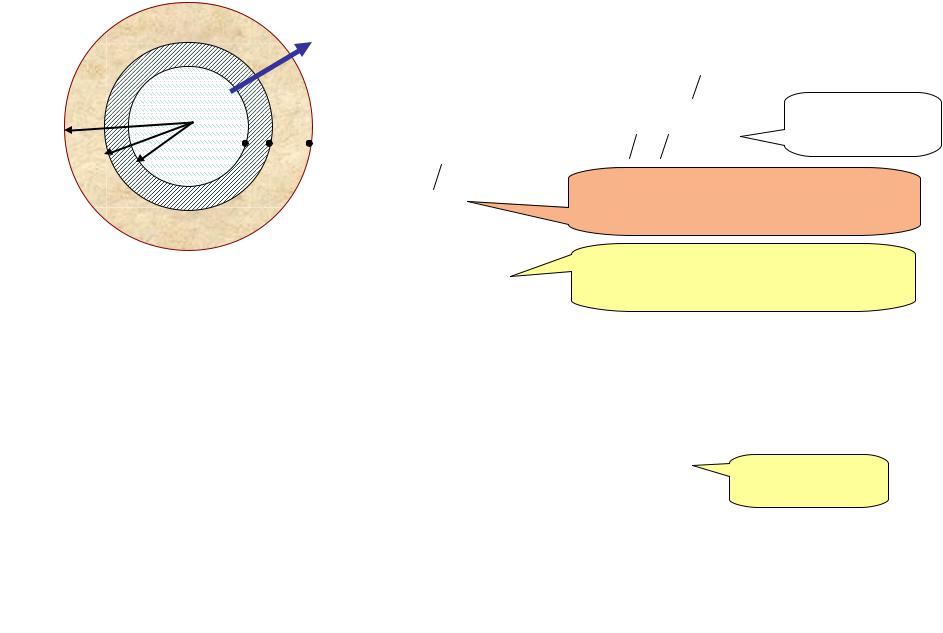
	В безразмерных переменных			T Te2
	В безразмерных переменных			Te1 Te2

Te1

Te2

d 2	1 d	0
d 2	d

r1r2 : dd Bi1 : dd Bi 1

C1 ln C2

C1 Bi C1 ln C2

C1 Bi C2 1

r	;	r	r	В качестве
r	;	r	r	масштаба выбран
r2		*	2	внешний радиус
r2

				цилиндра

(27)

(28)
	Bi 2r2	1

		2
(29)

(30)

Задание 1	А) Перейти аккуратно к безразмерным переменным
Задание 1	Б) Найти постоянные интегрирования из системы (30)
	Б) Найти постоянные интегрирования из системы (30)
	В) Построить для разных значений параметров	Bi и

l 2 r ln r

Принципы

последовательного и параллельного

соединений

термических

сопротивлений в цепь,

справедливые для плоской стенки в прямоугольной

системе координат, можно применить и для задачи о

теплопроводности в полом цилиндре.

Q dr l 2 r ln r

r 2 l,

В форме

ln r2 r1

2 l

закона Ома

ln r2

Термическое сопротивление

2 l

полого цилиндра

Жидкость течет в трубе,

Конвективное термическое

2 r1l

сопротивление жидкости

покрытой изоляционным

материалом

Имеем последовательное соединение конвективного сопротивления жидкости с двумя кондуктивными термическими сопротивлениями. Если задана температура жидкости и температура

внешней поверхности:

(31)

А)

full

2 r l

2 l

Сопротивление

1 1

изоляции

Если заданы температуры внутренней и внешней поверхностей

T T

(32)

Б)