
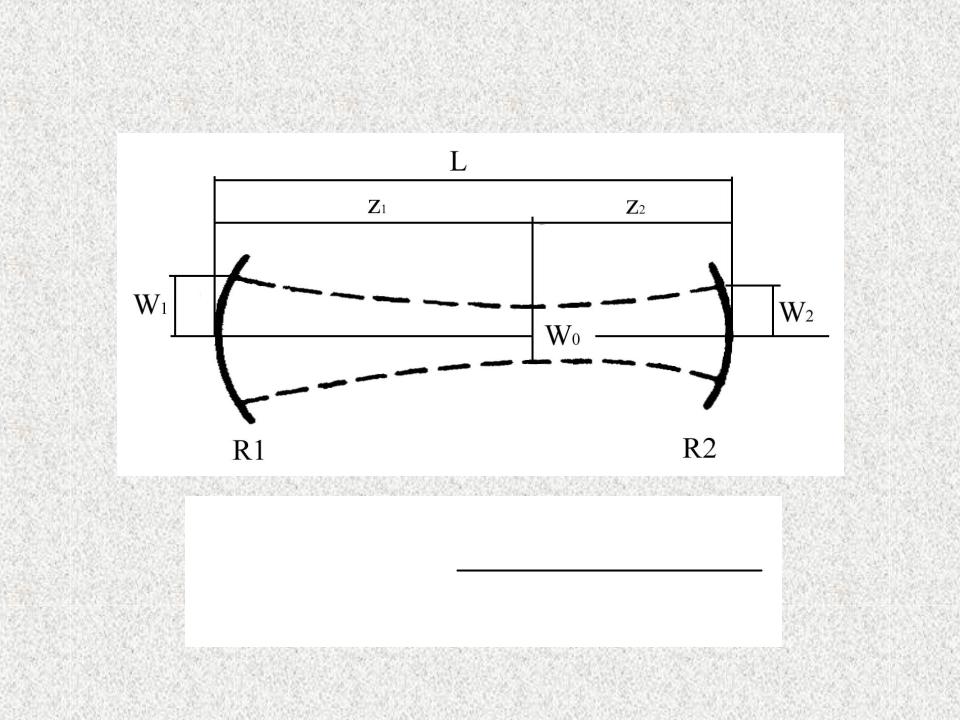
Параметры гауссова пучка
Размеры гауссова пучка на зеркалах:
|
|
2R |
2 |
|
(R L)L |
||
|
|
|
|
||||
W1(2) |
4 |
|
|
1(2) |
|
|
2(1) |
|
|
k |
L)(R1 R2 L) |
||||
|
|
|
|
(R1(2) |
|||

Параметры гауссова пучка
Нахождение положения и размера перетяжки
|
z1 |
|
z2 |
L |
|
|
|
|
|
2 |
|
|
|
|
z |
|
L(R2(1) L) |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1(2) |
|
R R L |
|
|
||||
|
|
|
|
|
|
|
( z ) |
|
|
|
|
|
|
|
|
|
|
||||||
W12 W02 1 |
|
|
12 |
|
|
|
|
|
|
|
|
1 2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
W0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
L)(R2 L)(R1 R2 L) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
4 |
L(R1 |
|||||||||
|
|
|
|
|
|
|
|
z2 |
|
|
W0 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
(R1 R2 2L) |
|||||||||||||
W2 |
2 |
W0 |
2 1 |
|
|
|
|
|
k |
|
|
||||||||||||
|
|
|
2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
W0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для конфокального резонатора: |
W |
2 |
|
λL , W |
2 λL , |
z |
L |
|
|||||||
|
|
|
|||||||||||||
|
1(2) |
|
|
|
|
π |
0 |
|
2π |
1(2) |
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для концентрического резонатора: |
W |
2 |
|
|
|
|
λR |
, W 2 |
|
λ |
L(2R L), |
||||
|
|
|
|
|
|
|
|||||||||
|
1(2) |
|
|
|
π |
2R / L 1 |
0 |
|
2π |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
|
z |
|
L |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1(2) |
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Эквивалентный конфокальный резонатор
ЭКР – резонатор, в котором поверхности равной фазы совмещены с поверхностями зеркал исследуемого резонатора. ЭКР используется для оценки приблизительного уровеня дифракционных потерь и пространственных характеристик гауссовых пучков
Радиус кривизны ЭКР: |
RЭКР LЭКР 2L |
g1g2 (1 g1g2 ) |
|
|||
g1 |
g2 |
2g1g2 |
||||
|
|
|||||
|
|
|
πW 2 |
|
L |
|
|
|
|
0ЭКР |
|
|
|
Расположение зеркал ЭКР: |
z1(2) |
|
|
|
|
|
λ |
2 |
|
||||
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
a2 |
|
g |
|
|
|
Число Френеля ЭКР: |
N1(2) |
|
1(2) |
1(2) |
(1 g g |
|
) |
|
|
|
|
2 |
|||||
|
ЭКР |
|
λL |
|
g2(1) |
1 |
|
|
|
|
|
|
|
|
|
||

Спектр мод резонатора
Ранее спектр продольных мод резонатора был получен из условия равенства длины резонатора целому числу длин полуволн электромагнитного поля
Для произвольной пространственной конфигурации электромагнитной волны, имеющей определенную фазу, условие существования стоячей волны в резонаторе формулируется так:
Разность фаз, соответствующая проходу волны через резонатор, должна быть кратной
Это приводит к изменению полученного ранее частотного спектра мод резонатора
Для продольных и поперечных мод получаются разные частоты, поскольку фазы этих типов колебаний разные
Спектр мод резонатора
Условие для нахождения частот продольных мод:
|
|
|
|
|
|
λz1 |
|
|
|
|
|
|
|
|
|
||
|
φ kL arctg |
|
|
|
arctg |
|
λz2 |
|
qπ |
|
|||||||
|
|
|
2 |
|
2 |
|
|||||||||||
|
|
|
|
|
πW |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
πW |
|
|
|
|
|||
|
|
|
|
|
0 |
|
|
0 |
|
|
|||||||
Частоты продольных мод: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
c |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
νq |
|
q |
|
arccos |
g1g2 , |
νq νq νq 1 |
|
|
|||||||||
|
|
L |
|||||||||||||||
|
2πL |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||
Частоты поперечных мод:
|
c |
|
1 m n |
|
|
|
c (m n) |
|
|
νqmn |
|
q |
|
arccos |
g1g2 , |
νmn |
|
|
arccos g1g2 |
|
|
L |
|||||||
|
2πL |
|
|
2 |
π |
|
|
||
Спектр мод конфокального резонатора: |
|
|||
|
c |
|
m n 1 |
|
νqmn |
|
q |
2 |
|
|
||||
|
2L |
|
||
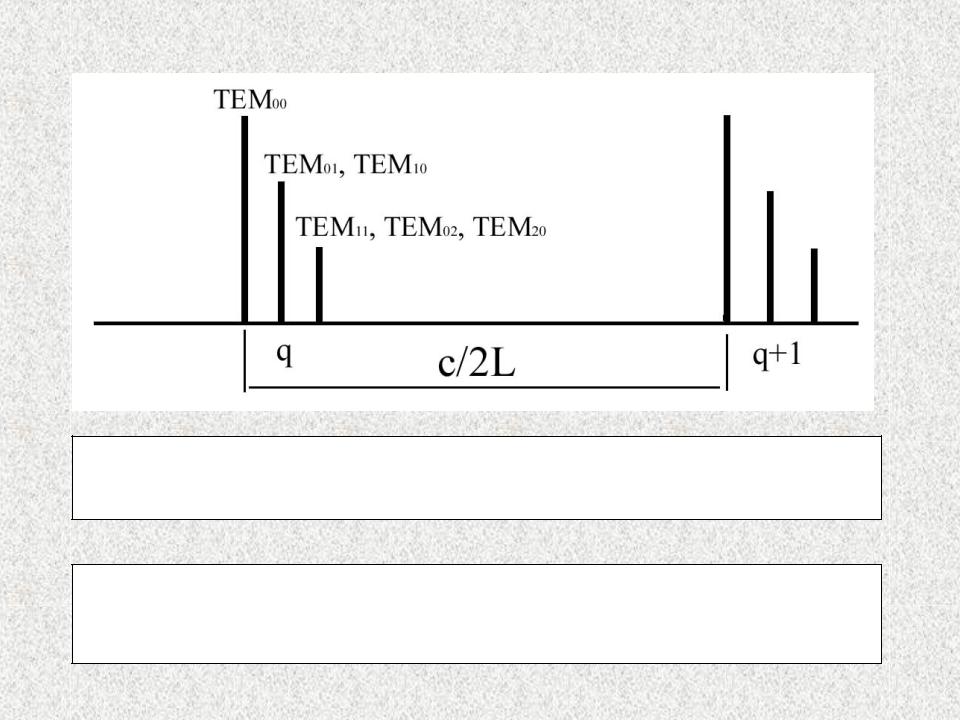
Спектр мод резонатора
При фиксированном значении m+n расстояние между соседними про- дольными модами составляет c/2L
При фиксированном значении q разность частот между поперечными модами определяется разностью. Поэтому частоты различных поперечных мод совпадают

Затягивание частоты
Моды резонатора имеют конечную спектральную ширину
Рассмотрим лазер, излучающей на одной моде, частота которой не совпадает с центральной частотой лазерного перехода
Найдем частоту генерации моды и ее ширину
Частота генерации имеет промежуточное значение между центральной частотой перехода и частотой моды резонатора
Частота генерации затягивается по направлению к центральной частоте
Как для однородно, так и для неоднородно уширенной линии частота генерации может быть определена одинаковым образом
Для вычисления частоты генерации можно использовать полуклассический подход
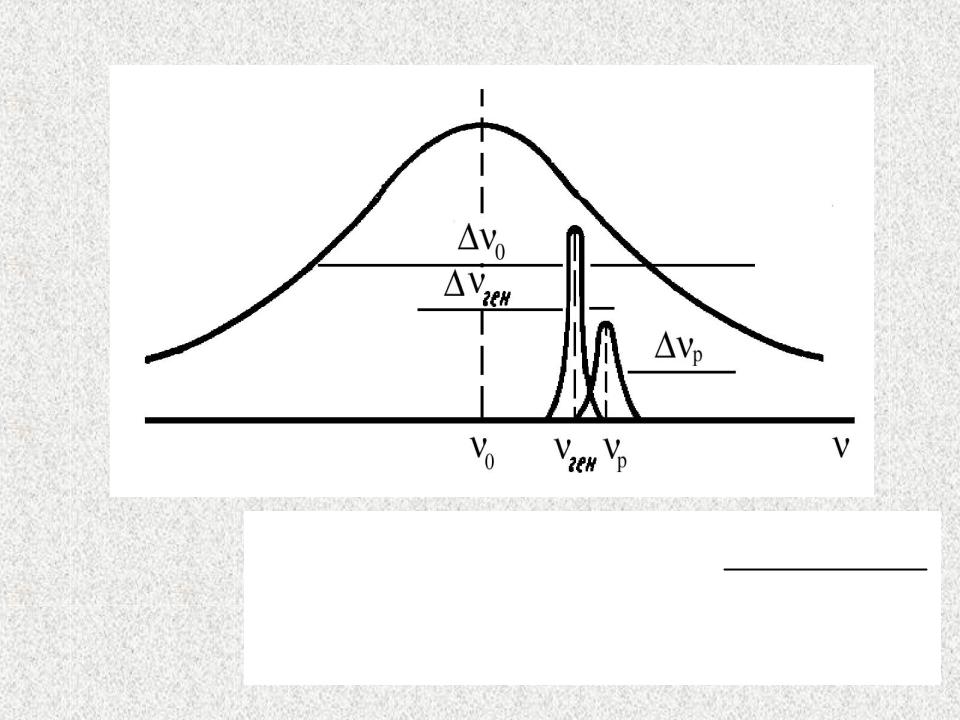
Затягивание частоты
|
|
|
|
ν |
0 |
/Δν +ν |
р |
/Δν |
p |
|
|
|
N2 |
2π |
2hν ( ν |
p |
)2 |
|
Частота генерации: |
ν |
ген |
= |
|
0ген |
|
|
, ν |
ген |
|
|
|
|
|||||
1/Δν +1/Δν |
p |
|
N |
P |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
0вых |
|
|
|
|
|
|
|
|
|
|
|
|
|
N N2 N1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Затягивание частоты
Пример для случая неоднородного уширения
Для большинства газовых лазеров величина 0 составляет порядка 1 ГГц, а для твердотельных может достигать 300 ГГц. В то же время, p
составляет единицы и десятки мегагерц
Следовательно, 0 p и затягивание частоты невелико
Пусть лазер излучает с выходной мощностью 1 мВт Пусть νген10 МГц Тогда на длине волны 633 нм νген меньше 1 Гц
Δνген /νген 10 15

Затягивание частоты
Пусть длина резонатора лазера составляет 1 м
|
|
Δν |
|
|
|
L |
|
|
|
|
|
|
|
||||
|
|
ν |
|
|
|
L |
|
|
Δνpр/ν 10 15 |
|
|
|
13 |
||||
L 10см |
||||||||
Эта ширина может быть |
|
|
|
Это ничтожно малое изменение |
||||
|
|
|
длины, приблизительно в 105 раз |
|||||
обусловлена изменением |
|
меньшее размера атома, уже приводит |
||||||
длины резонатора |
|
к изменению частоты моды резонатора |
||||||
и частоты генерации на величину порядка 1 Гц
На практике же длина резонатора меняется на много порядков больше, например, из-за вибрации или неоднородности температуры. Поэтому реальная ширина генерации оказывается существенно большей и составляет единицы и десятки килогерц
