Вопрос 7 - Способы задания булевых функций

Способы задания булевых функций.

1. Задание ф-ции таблицей истинности

2. Диаграммный способ

3. Аналитический способ

4. Числовые способы

5. Карточный способ

6. Кубический способ

7. На основе двоичной системы

1. Задание ф-ции таблицей истинности

Формальная логика занимается высказываниями с точки зрения их истинности.

В таблице истинности должны быть указаны все наборы и значения функций на этих наборах. Функции f ₆ и f ₉ представлены в таблице.

x1	x2	f6	f9
0	0	0	1
0	1	1	0
1	0	1	0
1	1	0	1

2. Диаграммный способ

Диаграммный способ предполагает диаграмму, для каждой переменной и диаграмму для функции. На диаграммах нужно выделять наборы. Достоинством диаграммного способа -наглядность, а недостаток - при большом количестве переменных диаграммы становятся слишком сложными.

Каждый участок служит для фиксирования набора.

Набор должен читаться ; должен совпадать с двоичными числами в столбце

f7

x1 x2 f7

0 0 1

0 1 1

1 0 1

1 1 0

3. Аналитические способы

Аналитические способы. Булевая функция может быть записана в виде формул. Известно четыре формы: СДНФ, СКНФ, ДНФ, КНФ.

С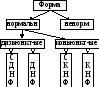ДНФ – совершенная дизьюктивная нормальная форма

ДНФ - дизьюктивная нормальная форма

КНФ - коньюктивная нормальная форма

Терм – составная часть формулы, выражения

Минтерм F_i x1x2...x_n

Макстерм Ф_i x1+x2... x_n

Форма называется нормальной, если она состоит из однотипных составляющих (термов). В зависимости от типа терма (дизъюнктивного или конъюнктивного) форма называется дизъюнктивной или конъюнктивной.

В качестве 1-го признака классификации используется однотипность используемых термов. Однотипность термов:

f = x1x2 + x1x2 f = (x1+x2) + x1x2

Ф F

F

В качестве 2-го критерия берется тип используемого терма.

В дизъюнктивно форме используются минтермы

f = x1x2 + x1x2 ДНФ

F_i F_j

В качестве следующего критерия используется совершенность терма.

Форма считается совершенной при использовании совершенных термов, включающих в себя все предусмотренные переменные. Если хотя бы один терм не является совершенным, то форма не может называться совершенной. Обычно такая форма получается после минимизации на основе тождеств склеивания.

Чтобы записать СДНФ, необходимо:

1) выделить в таблице истинности наборы, на которых функция равна 1;

для каждого выделенного набора оформить минтерм, равный 1;

полученные минтермы объединить знаком дизъюнкции.

Для оформления минтерма (конъюнкции) нужно действовать так:

1) перебирать разряды набора,

анализировать разряд, если разряд равен 1, то соответствующая переменная записывается без инверсии, в противном случае - с инверсией.

Чтобы записать СКНФ, необходимо:

1) выделить в таблице истинности наборы, на которых функция равна 0;

для каждого выделенного набора оформить макстерм, равный 0;

полученные макстермы объединить знаком конъюнкции.

Для оформления макстерма (дизъюнкции) нужно:

перебирать разряды набора,

анализировать разряд, если разряд равен 1, то соответствующая переменная записывается с инверсией, в противном случае – без инверсии.

4) Числовые способы

Числовой способ - сокращенный вариантом аналитической записи.

Для СДНФ числовая запись начинается с соединительного знака \/, левее которого внизу ставится 1. Эта единица означает, что минтермы должны быть равными единице. Правее соединительного знака записывается обозначение минтерма F, после чего в круглых скобках фиксируются наборы, на которых минтермы равны единице.

При числовом способе f_{26, СДНФ} = ₁VF_i(1,3,4), f_{129, СКНФ}= ₀ /\Фi(1, 2, 3, 4, 5, 6).

5) Карточный способ

Карточный и кубический способы. Что касается карточного и кубического способов задания, то СКНФ нужно перевести в СДНФ, так как при этих способах чаще используется СДНФ. Каждую заданную функцию надо представить в таблице истинности или числовым способом.

При карточном представлении каждый квадрат соответствует определенному набору.

6) Кубический способ

Кубическое представление основано на том, что каждой вершине куба соответствует свой набор. Естественно, что в начале координат будет набор 000, в близи координаты х₁ – набор 100, в близи координаты х₂ – набор 010, в близи координаты х₃ – набор 001. Естественно, что кубическое представление заданной функции будет таким, которое показано на рисунке.