
- •"Томский политехнический университет"
- •Матрицы, определители, системы линейных уравнений Метод окаймляющих миноров нахождения ранга матрицы
- •Алгоритм приведения матрицы к ступенчатому виду элементарными преобразованиями
- •Вычисление определителей
- •Действия над матрицами
- •Исследование и решение произвольной системы линейных уравнений
- •Блок-схема исследования и решения произвольной системы линейных уравнений
- •Элементы векторной алгебры
- •Геометрия прямых и плоскостей в таблицах Уравнения плоскости р в трехмерном пространстве r3 и уравнения прямой l в двухмерном пространстве r2
- •Уравнения прямой l в трехмерном пространстве r3 и в двухмерном пространстве r2
- •Взаимное расположение плоскостей p в трёхмерном пространстве r3 и прямых l в двухмерном пространствеR2
- •Расстояния d(p1,p2) между плоскостями p1 и p2 и d(l1,l2) между прямыми l1 и l2 в r3, пересечение pl плоскости p и прямой l в r3
- •Полярная система координат
- •Вычисление пределов
- •Предел дробно-рациональной функции
- •Сравнение бесконечно малых функций
- •Правила дифференцирования
- •8. Логарифмическое дифференцирование
- •Приложения производной Раскрытие неопределенностей по правилу Лопиталя
- •Исследования функции без применения производных
- •Исследования функции с применением производных
- •Неопределенный интеграл Метод непосредственного интегрирования
- •Метод интегрирования по частям
- •План интегрирования рациональных дробей
- •Интегрирование тригонометрических и гиперболических функций
- •Интегрирование иррациональностей
- •Приложения определенного интеграла
- •Дифференциальное исчисление функции нескольких переменных (фнп)
- •Интегральное исчисление функций нескольких переменных Интегралы от скалярной функции
- •Вычисление кратных интегралов
- •Криволинейные и поверхностные интегралы I-го рода.
- •Криволинейные и поверхностные интегралы II-го рода (по координатам).
- •Элементы теории поля
- •Дифференциальные уравнения, системы дифференциальных уравнений Дифференциальные уравнения первого порядка
- •Дифференциальные уравнения первого порядка
- •Дифференциальные уравнения высших порядков
- •Дифференциальные уравнения высших порядков
- •Системы дифференциальных уравнений
- •Системы дифференциальных уравнений
- •Системы дифференциальных уравнений
- •Функции комплексного переменного
- •Вычисление некоторых интегралов при помощи вычетов
- •Некоторые разложения в степенные ряды
- •Операционное исчисление
- •Теория вероятностей и математическая статистика
- •Некоторые непрерывные распределения
- •Интервальная оценка числовых характеристик
- •Сравнение двух средних генеральных совокупностей.
- •Сравнение двух средних генеральных совокупностей.
- •Методы вычислений Методы простой итерации и Зейделя решения систем линейных уравнений Пусть дана система линейных алгебраических уравнений, записанная в виде
- •Интерполяционные многочлены Лагранжа и Ньютона
- •Теоретическое обоснование методов хорд и касательных решения трансцендентных уравнений .
- •Литература
- •Предметный указатель
- •Содержание
Системы дифференциальных уравнений
|
№ |
Тип системы |
Вид системы |
Признак системы |
Метод решения системы |
|
2 |
Нормальная
линейная однородная система
(НЛОС). |
Коэффициенты
линейных комбинаций искомых функций
зависят от аргумента
|
Ур-я записаны явно отн-но первых производных; правые части уравнений представляют собой линейные комбинации искомых функций. |
Метод исключения неизвестных (см. НСДУ). Фундаментальной
системой решений НЛОС называется
совокупность произвольных
Если
|
|
3а |
Нормальная
линейная однородная система
|
Коэффициенты линейных комбинаций искомых функций постоянны.
|
Уравнения записаны явно относительно первых производных; правые части уравнений представляют собой линейные комбинации искомых функций. |
Матричный
метод. Из
характеристического уравнения
|
Системы дифференциальных уравнений
|
3б |
Нормальная
линейная однородная система
|
Коэффициенты линейных комбинаций искомых функций постоянны.
|
Ур-я записаны явно от-но первых производных; правые части уравнений представляют собой линейные комбинации искомых функций. |
Матричный
метод. Из
характеристического уравнения
|
|
3в |
Нормальная
линейная однородная система
|
Коэффициенты линейных комбинаций искомых функций постоянны.
|
Уравнения записаны явно относительно первых производных; правые части уравнений представляют собой линейные комбинации искомых функций. |
Матричный
метод. Если
в)
|

Нет Да Нет Да Нет Да![]()
![]()

























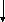

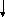
















абсолютно






Ф
![]()
ТВТ©ТПУВМ05
Ряд
Ряд
В
каждой точке z
D На
границе Dсоответствующий
числовой ряд исследуется отдельно Ряды
степеней
n≥0 Ряд
Тейлора n
= 0,1,2,… – правильная
часть Ряд
Лорана Четное
продолжение Ряды
Фурье n-целое n
= 0,1,2,.. Условия
Дирихле f(x)-периодическая,T=2ℓ; f(x)-кусочно-непрерывная
на любом конечном [x1,x2]
и может иметь разрывы толькоIрода; f(x)-кусочно-монотонная в
х0 - т.р. I
рода Нечетное
продолжение Сходится
внутри круга z-z0
<R абсолютно
и равномерно по т.Абеля R=z1-z0
,z1 –ближайшая
кz0изолированная
особая точка
n
< 0 – главная
часть Сходится
внутри кольца
r<
z-z0
<R Сходится
вне круга
r<
z-z0
S(x)–непрерывна в области сходимостиD Ряд
можно почленно дифференцировать любое
число раз в D Ряд
можно почленно интегрировать по любой
кривой L
Dлюбое число раз. да нет![]() сходится вD
сходится вD![]() расходится
вD
расходится
вD![]()
![]() и
другие признаки сходимости числовых
рядов
и
другие признаки сходимости числовых
рядов![]()
![]()
![]()

![]()
![]()

![]() и
другие признаки сходимости числовых
рядов
и
другие признаки сходимости числовых
рядов




























 –матрица из
коэффициентов при искомых функциях.
–матрица из
коэффициентов при искомых функциях.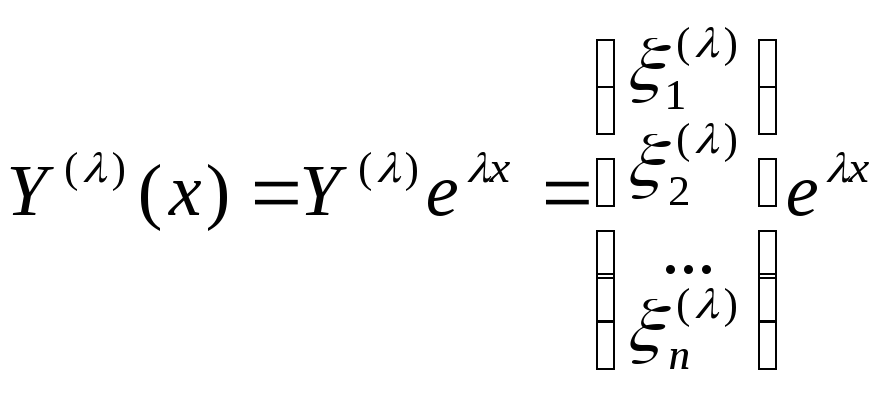 ,
где
,
где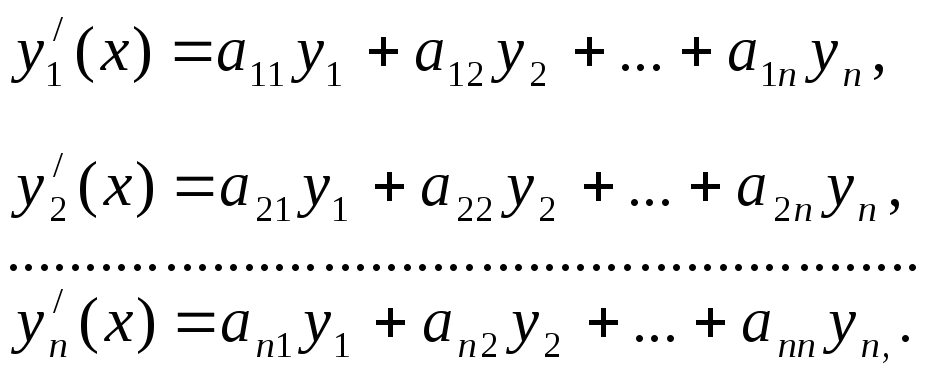
 –матрица из
коэффициентов при искомых функциях.
–матрица из
коэффициентов при искомых функциях.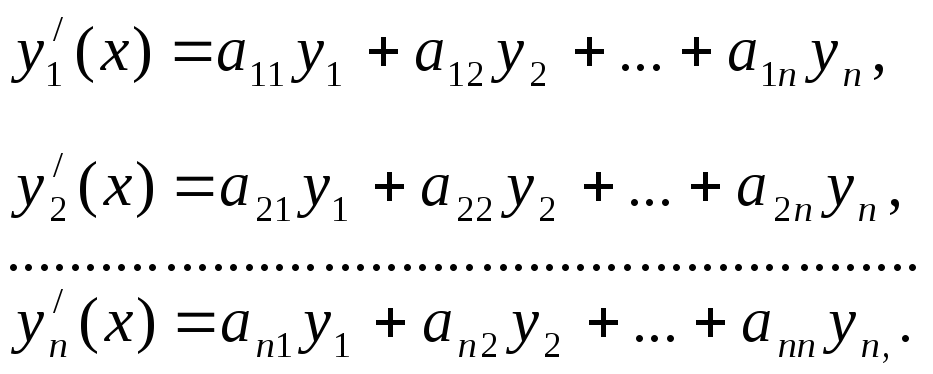
 –матрица из
коэффициентов при искомых функциях.
–матрица из
коэффициентов при искомых функциях.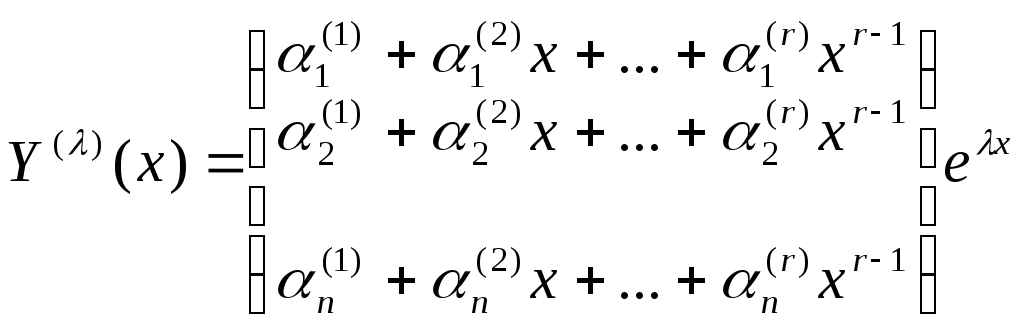 (),
коэффициенты которого
(),
коэффициенты которого