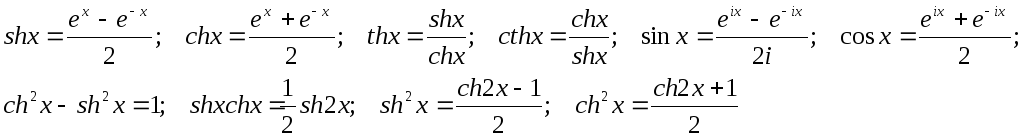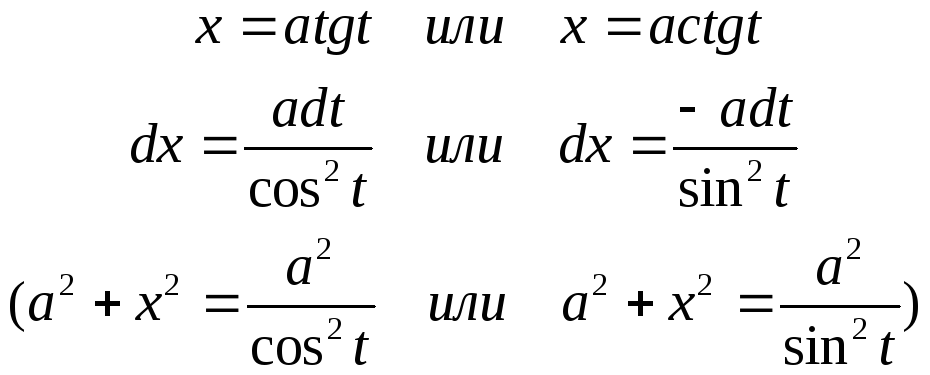- •"Томский политехнический университет"
- •Матрицы, определители, системы линейных уравнений Метод окаймляющих миноров нахождения ранга матрицы
- •Алгоритм приведения матрицы к ступенчатому виду элементарными преобразованиями
- •Вычисление определителей
- •Действия над матрицами
- •Исследование и решение произвольной системы линейных уравнений
- •Блок-схема исследования и решения произвольной системы линейных уравнений
- •Элементы векторной алгебры
- •Геометрия прямых и плоскостей в таблицах Уравнения плоскости р в трехмерном пространстве r3 и уравнения прямой l в двухмерном пространстве r2
- •Уравнения прямой l в трехмерном пространстве r3 и в двухмерном пространстве r2
- •Взаимное расположение плоскостей p в трёхмерном пространстве r3 и прямых l в двухмерном пространствеR2
- •Расстояния d(p1,p2) между плоскостями p1 и p2 и d(l1,l2) между прямыми l1 и l2 в r3, пересечение pl плоскости p и прямой l в r3
- •Полярная система координат
- •Вычисление пределов
- •Предел дробно-рациональной функции
- •Сравнение бесконечно малых функций
- •Правила дифференцирования
- •8. Логарифмическое дифференцирование
- •Приложения производной Раскрытие неопределенностей по правилу Лопиталя
- •Исследования функции без применения производных
- •Исследования функции с применением производных
- •Неопределенный интеграл Метод непосредственного интегрирования
- •Метод интегрирования по частям
- •План интегрирования рациональных дробей
- •Интегрирование тригонометрических и гиперболических функций
- •Интегрирование иррациональностей
- •Приложения определенного интеграла
- •Дифференциальное исчисление функции нескольких переменных (фнп)
- •Интегральное исчисление функций нескольких переменных Интегралы от скалярной функции
- •Вычисление кратных интегралов
- •Криволинейные и поверхностные интегралы I-го рода.
- •Криволинейные и поверхностные интегралы II-го рода (по координатам).
- •Элементы теории поля
- •Дифференциальные уравнения, системы дифференциальных уравнений Дифференциальные уравнения первого порядка
- •Дифференциальные уравнения первого порядка
- •Дифференциальные уравнения высших порядков
- •Дифференциальные уравнения высших порядков
- •Системы дифференциальных уравнений
- •Системы дифференциальных уравнений
- •Системы дифференциальных уравнений
- •Функции комплексного переменного
- •Вычисление некоторых интегралов при помощи вычетов
- •Некоторые разложения в степенные ряды
- •Операционное исчисление
- •Теория вероятностей и математическая статистика
- •Некоторые непрерывные распределения
- •Интервальная оценка числовых характеристик
- •Сравнение двух средних генеральных совокупностей.
- •Сравнение двух средних генеральных совокупностей.
- •Методы вычислений Методы простой итерации и Зейделя решения систем линейных уравнений Пусть дана система линейных алгебраических уравнений, записанная в виде
- •Интерполяционные многочлены Лагранжа и Ньютона
- •Теоретическое обоснование методов хорд и касательных решения трансцендентных уравнений .
- •Литература
- •Предметный указатель
- •Содержание
Интегрирование тригонометрических и гиперболических функций
|
№ п/п |
Подынтегральная функция |
Подстановка |
Вспомогательные преобразования |
Итог |
|
1 |
sin x, cos x |
Универсальная
|
|
Подынтегральная функция рациональная относительно х |
|
2 |
Нечетная относительно сos x |
|
| |
|
3 |
Нечетная относительно sin x |
|
| |
|
4 |
Четная относительно сos x и sin x |
|
| |
|
|
| |||
|
5 |
Степени четные неотрицательные |
|
Понижение степени | |
|
6 |
|
|
Сумма функций | |
|
7 |
Интегрирование гиперболических функций аналогично интегрированию тригонометрических функций
| |||
Интегрирование иррациональностей
|
|
Подынтегральная функция |
Подстановка |
Итог | |
|
1 |
R
– рациональная
функция,
|
|
Рациональная
функция
| |
|
2 |
|
|
Рациональная
функция
| |
|
|
| |||
|
|
| |||
|
3 |
Дифференциальный бином
|
p ─ целое число, m,n ─ дроби |
|
Рациональная
функция
|
|
|
| |||
|
|
| |||
|
4 |
|
|
См. пункт 5 | |
|
5 |
|
|
Два табл-х инт-ла | |
При нахождении первообразной функции можно пользоваться следующим алгоритмом:
Попытаться применить непосредственное интегрирование;
Если это не удается, определить класс функции (рац. дробь, тригонометрическая, иррациональная) и применить соответствующие подстановки, а если функция смешанных классов – интегрирование по частям.
Приложения определенного интеграла
Теорема. Если величинаQобладает на [a,b]
свойством аддитивности, а именно, если a = x0 x1 x2 … xn = b,
то Q=Q1+Q2+…+Qn, гдеQi – значениеQ на [xi-1,xi],i=1,2,…n;
свойством линейности Qв малом:Q f(x)x, гдеf(x) – интегрируемая на[a,b] функция,
то величину Q можно найти интегралом от ее элементаdQ = f(x)dx по промежутку [a,b]:
![]()
|
Q |
№ |
Чертеж |
Система координат и пояснения |
Формула |
Q |
|
S, п л ощ а д ь
п л о с к о й
ф и г у р ы
D |
1 |
|
Д. С. К.
Одна кривая границы области D не выше другой. |
|
S, п л о щ а д ь
п л о с к о й
ф и г у р ы
D |
|
2 |
|
Д. С. К.
Одна кривая границы области D не левее другой. |
| ||
|
3 |
|
Д. С. К. t x()=a, x()=b ( y(t)0, t [, ] ) Верхняя граница области задана параметрически |
| ||
|
4 |
α β ρ1(φ) ρ2(φ) |
П. С. К.
|
| ||
|
д л и н а
к р и в о й
L |
1 |
|
Д. С. К.
|
|
д л и н а
к р и в о й
L |
|
2 |
Д. С. К.
|
| |||
|
3 |
|
Д. С. К.
Линия L задана параметрически |
| ||
|
4 |
ρ(φ) β
α
|
П. С. К.
|
|
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
|
Q |
№ |
Чертеж |
Система координат и пояснения |
Формула |
Q |
|
V, о б ъ е м
т е л а
Т |
1 |
|
Д. С. К.
|
|
V, о б ъ е м
т е л а
Т |
|
2 |
|
Д. С. К.
Тело Т образовано вращением кривой у=f(х) вокруг оси 0Х |
| ||
|
, п л ощ а д ь
п о в е р х н. ω |
1 |
|
Д. С. К.
Поверхность образована вращением кривой у=f(х) вокруг оси 0Х |
|
, п л о щ а д ь
п о в е р х н. |
|
Д. С. К.
Поверхность образована вращением кривой у=f(х (t)), заданной параметрически, вокруг оси 0Х |
| ||||
|
S, п у т ь |
1 |
|
Д. С. К.
V – скорость прямолинейного движения тела на промежутке времени [t1,t2] |
|
S, п у т ь |
|
А, р а б о т а |
1 |
|
Д. С. К.
Сила F направлена параллельно оси 0Х на промежутке [a,b] |
|
А, р а б о т а |
|
Р,д а в л
|
1 |
|
Д. С. К.
– плотность жидкости, давящей на пластину D |
|
Р, д а в л.
|
|
m,м а с с а |
1 |
|
Д. С. К.
– линейная плотность кривой L |
|
m,м а с с а |
Статические моменты относительно координатных осей Sx,Sy,, моменты инерцииМх,, Му, координаты центра тяжестихс, ус плоской кривой