1.3. Погрешности измерений

Погрешность измерения – это отклонение результата измерения от действительного значения измеряемой величины.

Погрешность классифицируется по различным признакам. Общая классификация погрешностей измерения приведена на рис. 1.3.

Погрешности

измерения

-Ожидаемые;

-Грубые;

-Промах.

Рис. 1.3. Классификация погрешностей измерения

Систематической погрешностью измерения называется составляющая погрешности измерения, которая остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины. Если при выполнении ряда измерений одной и той же величины между отдельными результатами измерений имеются различия, которые невозможно предсказать, а какие-либо присущие им закономерности проявляются лишь при значительном числе результатов, то такую погрешность называют случайной.

Качество измерений, отражающее близость к нулю систематических погрешностей результатов измерений, называют правильностью измерений.

Качество измерений, отражающее близость результатов измерений, выполненных в одних и тех же условиях, называют сходимостью измерений.

Говоря о случайных погрешностях, необходимо различать ожидаемую погрешность, грубую погрешность и промах.

18

Ожидаемая погрешность – погрешность, получаемая в результате специально созданных условий измерения.

Грубая погрешность – погрешность, существенно превышающая погрешность, оправданную условиями измерения, свойствами средств измерения и т.д. Такие погрешности могут возникать, например, вследствие резкого кратковременного изменения напряжения в сети питания.

Грубые погрешности обнаруживают с помощью статистических методов и обычно исключают из результата.

Промахи – погрешность измерения, явно и резко искажающая результат измерения. [5]

Статические и динамические погрешности различают по их зависимости от скорости изменения измеряемой величины во времени. Погрешности, не зависящие от этой скорости, называются статическими. Погрешности, отсутствующие, когда эта скорость близка к нулю, и возрастающие при ее отклонении от нуля, называются динамическими. [6]

Методическая погрешность возникает вследствие недостаточной разработанности теории тех явлений, которые положены в основу измерения, и неточности тех соотношений, которые используются для нахождения оценки измеряемой величины.

Погрешность оператора представляет собой субъективную погрешность наблюдателя, например, в случае неправильного отсчитывания долей шкалы прибора. Нужно отметить, что совершенствование конструкций отсчетных устройств приводит к уменьшению этого типа погрешности, а в случае использования цифровых приборов она вообще исчезает.

Погрешность от влияющих величин обусловлена воздействием на элементы процесса измерения влияющих физических величин.

Погрешность при статистической обработке данных возникает вследствие округления и др. действий при статистическом анализе экспериментальных данных.

Инструментальная погрешность возникает вследствие несовершенства средств измерения. [5]

Составляющая погрешности, определяемая погрешностью средства измерения, является наибольшей и включает в себя составляющие инструментальной погрешности. Классификация инструментальных погрешностей приведена на рис. 1.4.

В зависимости от условий появления различают основную и дополнительную погрешности. Основная погрешность – погрешность, возникающая в нормальных условиях работы прибора, оговоренных в технической документации. Изменения показаний вследствие отклонения условий эксплуатации от нормальных называются дополнитель-

19

ными погрешностями и нормируются указанием коэффициентов влияния изменения отдельных влияющих величин на изменение показаний.

Инструментальная

погрешность

Рис. 1.4. Классификация составляющих инструментальной погрешности

Абсолютная погрешность представляет собой разность измеренного и действительного значений измеряемой величины

где X П – измеренное значение физической величины;

X Д – действительное значение физической величины.

Абсолютная погрешность измеряется в единицах измерения измеряемой физической величины.

Абсолютная погрешность не может служить показателем точности измерений, так как одно и то же ее значение, например, t 0,05°С при

t = 100 °С, соответствует достаточно высокой точности, а при t = 1 °С – низкой. Поэтому для характеристики точности результатов измерения вводится понятие относительной погрешности, выражаемой в относительных единицах или процентах:

20

Однако относительная погрешность не может быть использована для нормирования погрешности средств измерений, т.к. при различных значениях измеряемой величины принимает различные значения вплоть до при XП 0 . Поэтому для указания и нормирования погрешно-

сти средств измерения используется приведенная погрешность. Она определяется как отношение абсолютной погрешности к разности между верхним и нижним пределами измерения средства измерения:

где X В – значение верхнего предела измерения средства измерения; X Н – значение нижнего предела измерения средства измерения.

Ее основное отличие от относительной погрешности состоит в том, что абсолютная погрешность относится не к переменному текущему значению измеряемой величины, а к постоянной величине диапазона измерения. [5]

В зависимости от изменения значения измеряемой величины погрешности разделяют на аддитивную, мультипликативную, гистерезисную.

Определение мультипликативной погрешности наглядно иллюстрирует рис. 1.5.

На рисунке представлено две зависимости показаний измерительного прибора Y от значения измеряемой величины Х. Цифрой 1 обозначена номинальная зависимость, определенная в технической документации, цифрой 2 – реальная зависимость, полученная в текущих

21

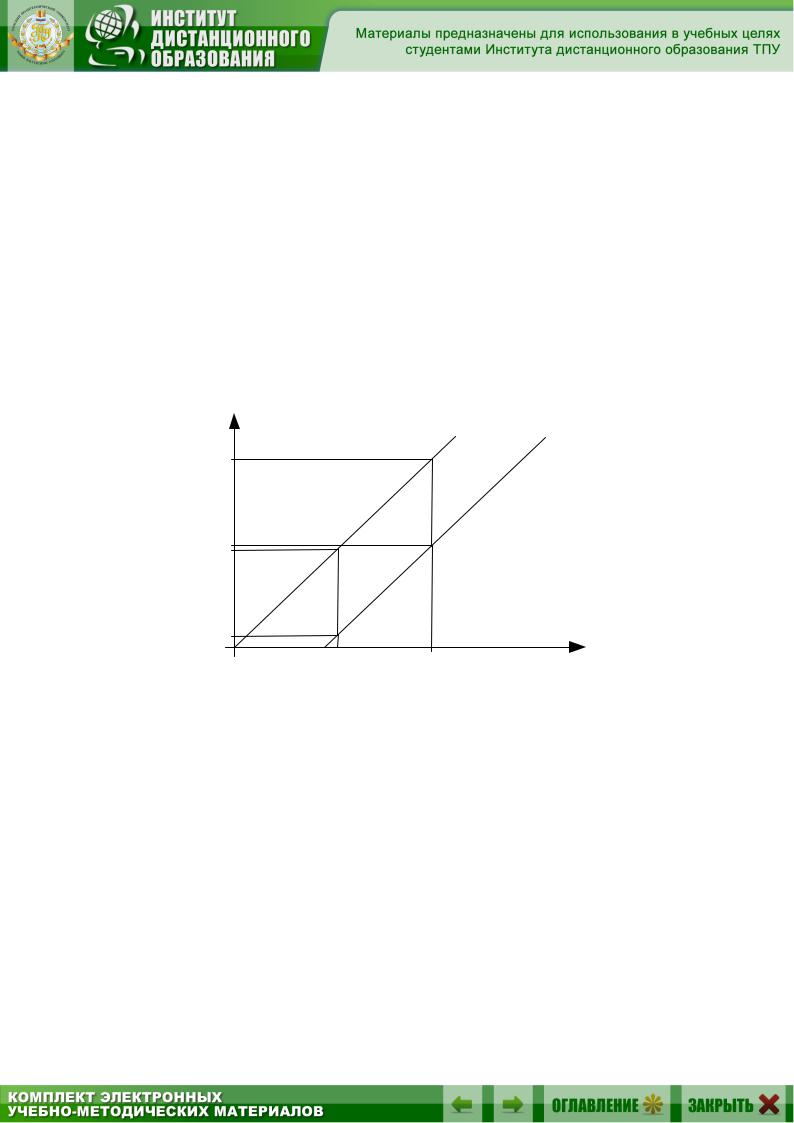
условиях эксплуатации. При измерении значения физической величины Х1 в текущих условиях эксплуатации с помощью измерительного прибора получаем значение Y1P, отличающееся от номинального значения Y1Н на величину абсолютной погрешности 1 Y1P X1H . При измере-

нии значения физической величины Х2 (при этом Х1 < Х2) в текущих условиях эксплуатации с помощью измерительного прибора получаем значение Y2P, отличающееся от номинального значения Y2Н на величину абсолютной погрешности 2 Y2P X2H . Очевидно, что при увеличе-

нии значения измеряемой величины Хi увеличивается погрешность измерения. Погрешность, увеличивающаяся с увеличением значения измеряемой величины, называется мультипликативной.

Погрешность, не изменяющаяся с изменением значения измеряемой величины (рис. 1.6), называется аддитивной.

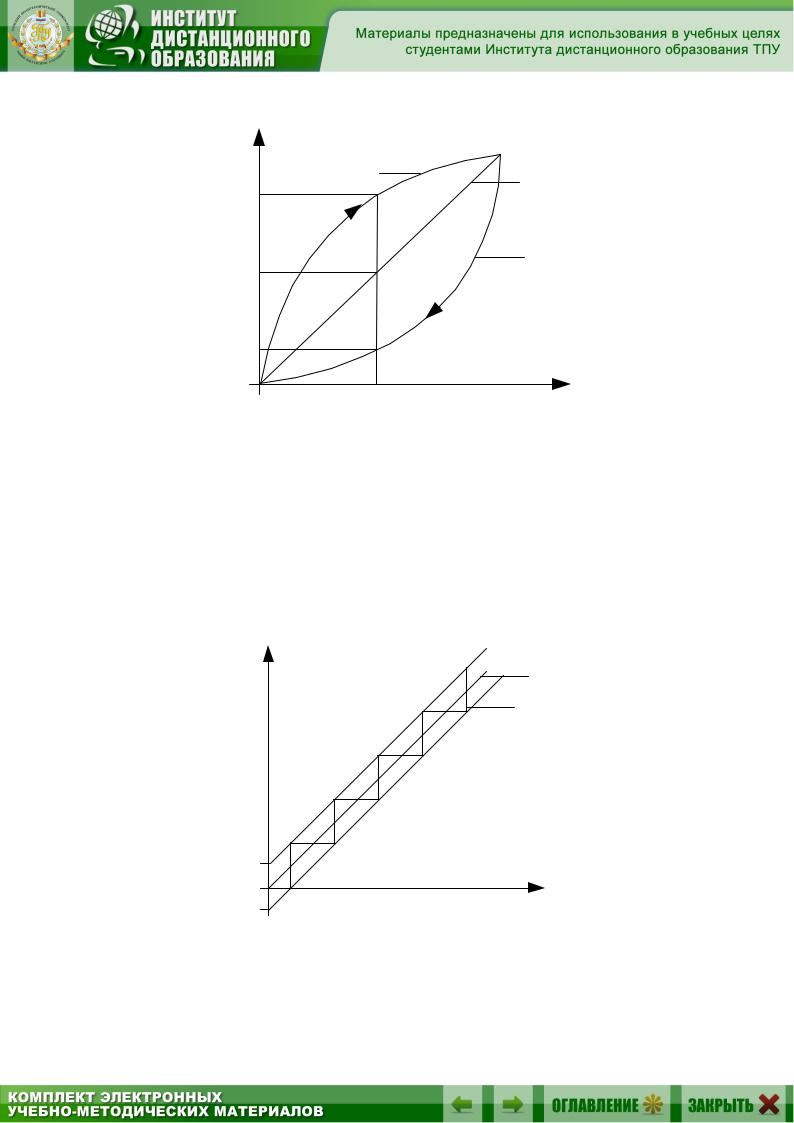
Наиболее существенной и трудно устранимой погрешностью измерительного устройства является погрешность гистерезиса, выражаемая в несовпадении реальных функций преобразования при увеличении и уменьшении значения измеряемой величины и номинальной функции преобразования.

На рис. 1.7 цифрой 1 обозначена номинальная функция преобразования, следовательно, при значении измеряемой величины Х1 показания прибора должны составлять Y1. При увеличении значения измеряемой величины (прямой ход) показания прибора (кривая 2) составляют Y1пх, а при уменьшении (кривая 3) – Y1ох. Таким образом, при измерении одного и того значения Х1 показания прибора отличаются друг от друга (Y1пх Y1пх) и от номинального значения.

22

Номинальной статической характеристикой цифрового преобразователя считают прямую (рис. 1.8, прямая 1), реальная статическая характеристика цифрового преобразователя (рис. 1.8, кривая 2) представляет собой ступенчатую кривую. Текущая разность между номинальной и реальной характеристиками составляет погрешность квантования. Границы полосы погрешности квантования показаны на рис. 1.8 штриховыми линиями. [6].

23

Погрешность квантования – это специфическая разновидность погрешности, возникающая в цифровых приборах и дискретных преобразователях. Например, при плавном изменении напряжения в пределах от 0 до 0,5 мВ показания цифрового вольтметра с пределом измерения 1000 мВ и шагом квантования 1 мВ будут составлять 0 мВ, а при превышении значения 0,5 мВ показания будут составлять 1 мВ.

Контрольные вопросы и задания

1.Что называется погрешностью измерений? По каким признакам она классифицируется?

2.В чем заключается отличие между грубой погрешностью и промахом?

3.Объясните причины возникновения инструментальной погреш-

ности.

4.Определите, в каких пределах находится действительное значение напряжения, если его величина измеряется с помощью вольтметра, имеющего предел измерения 0…30 В с приведенной погрешностью 2 %, показания вольтметра составляют 18 В.

5.Определите, в каких пределах находится действительное значение давления питательной воды, если показания манометра составляют 15,2 МПа с относительной погрешностью 0,5 %.

6.Назовите погрешность, которую называют погрешностью прямого хода, объясните, почему.

7.Каким образом можно уменьшить погрешность квантования?

24