
От Готмана на 8 семестр(Эл. энерг. СиС) / Задачн. (УП) 2010 Реж. КЗ в ЭЭСС
.pdf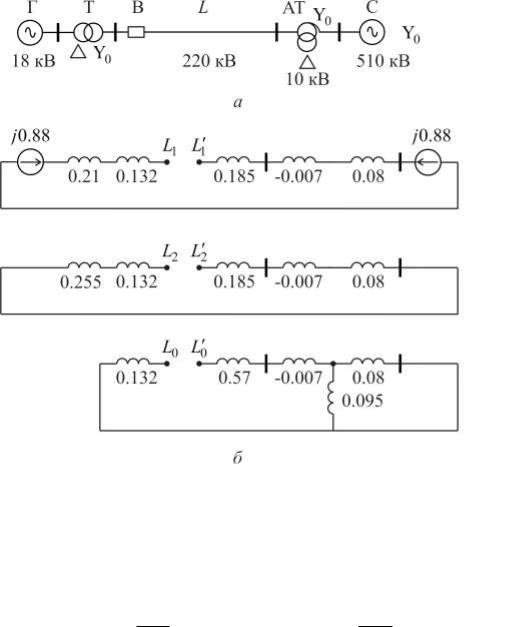
1
2
0
Рис. 3.1. К примеру 3.1: а – исходная схема; б – схемы замещения прямой (1), обратной (2) и нулевой (0) последовательностей
Решение. Расчеты осуществляем в относительных единицах при следующих базисных условиях:
Тогда
U б 2
Sб = 176.5 МВА, |
||||
18 |
242 |
242 |
кВ, |
|
18 |
||||
|
|
|
||
Uб 1
U б 3
=18 кВ.
242 525220 577. 5 кВ.
1. Расчет параметров схем замещения
На рис. 3.1, б приведены схемы замещения прямой, обратной и нулевой последовательностей с реактивностями в относительных единицах при выбранных базисных условиях. Результирующие сопротивления указанных схем относительно места разрыва составляют:
xL1Σ
xL2Σ
xL0Σ
0.21 + 0.132 + 0.185 – 0.007 + 0.08 = 0.6;
0.255+0.132+0.185 – 0.007 + 0.08 = 0.645;
0.132 + 0.57 – 0.007 + 0.08 // 0.095 = 0.74.
81

Считаем, что при включении генератора на параллельную работу напряжение на выключателе со стороны системы равно напряжению системы, которое в о. е. составляет
U |
|
|
j510 |
j0. 88. |
||
С |
577. 5 |
|||||
|
|
|
||||
|
|
|
|
|||
В режиме холостого хода сверхпереходная ЭДС генератора равна |
||||||
|
|
|
|
= j0.88. |
||
напряжению на выключателе, т. е. Е |
||||||
Наиболее тяжелые условия по току имеют место, когда напряжения включаемых источников находятся в противофазе. При этом результирующая ЭДС схемы прямой последовательности относительно места разрыва составит
E1Σ
E
UС
= j0.88 – (– j0.88) = j1.76.
2. Расчет токов при включении источников питания (генератора и системы) на параллельную работу
2.1. Одновременное включение трех фаз представляет симметричный режим:
|
3 |
|
|
E |
|
|
j1. |
76 |
2. 93. |
|
I |
|
|
|
|
|
|||||
L |
|
|
j x |
L1 |
|
j0 |
. 6 |
|
||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
2.2. При включении двух фаз (разрыв одной фазы) имеем:
x |
(1) |
xL2Σ / / xL0Σ 0.645/ / 0.74 |
0.345 . |
|
L |
||||
|
|
|
Рассчитываем симметричные составляющие тока прямой и обратной последовательностей по месту включения:
|
|
|
E |
|
|
|
|
1. 76 |
I |
L1 |
|
1Σ |
|
|
|
|
|
|
x |
(1) |
|
(0. 6 0. 345) |
||||
|
j(x |
|
) |
|
||||
|
|
|
|
|||||
|
|
L1Σ |
|
|
||||
|
|
|
|
|
|
|
||
1. 86
;
|
|
|
|
x |
(1) |
|
0.345 |
|
|
I |
|
I |
|
|
1.86 |
1. |
|||
L2 |
L1 |
x |
|
0.645 |
|||||
|
|
|
|
|
|
||||
|
|
|
|
L2Σ |
|
|
|||
|
|
|
|
|
|
|
|
||
Модуль сверхпереходного тока в здоровых фазах В и С по месту включения составляет:
|
I |
1 |
L |
LC |
m |
1 I |
L1 |
1.5 1.86 2.79 |
, |
|||||
|
|
LB |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
m 1 |
|
|
|
|
|
0. 645 0. 74 |
|
|
|
||||
где |
3 1 |
|
1. 5. |
|
||||||||||
|
|
|
|
|
||||||||||
(0. 645 0. 74) 2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Симметричные составляющие тока прямой и обратной последовательностей в цепи генератора (нулевая – отсутствует),с учетом перехода
82

через трансформатор со схемой соединения обмоток тываются по выражениям:
Y0
/
11
, рассчи-
токи
I |
Г1 |
I |
e |
j30 |
11 |
1.86e |
j330 |
1.86e |
j30 |
; |
|||||
|
|
|
|
|
|
||||||||||
|
|
L1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
Г2 |
I |
L2 |
e |
j30 |
11 |
1e |
j(180 330) |
1e |
j150 |
. |
|
|||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Наибольшего значения ток генератора достигает в фазе В, |
где |
|||||||||||||
I Г1и |
I Г2 |
совпадают по фазе: |
|
|
|
|
||||||||
|
|
|
|
2 |
|
|
|
|
|
j(2 4 0 30) |
|
j(1 20 1 50) |
|
|
|
I |
|
1 |
a |
|
I |
|
aI |
|
1 . 86e |
|
1e |
|
|
|
Г В |
|
Г1 |
Г2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
1 . 86e |
j2 7 0 |
1e |
j2 7 0 |
2 . 86e |
j2 7 0 |
. |
|
|
|
2.3. При включении только одной фазы (разрыв двух фаз) имеем следующие значения дополнительной реактивности и симметричных составляющих токов трѐх последовательностей:
x |
2 |
x |
L2Σ |
x |
L0 Σ |
(0 . 645 0 . 74) 1 . 385; |
|||||||
L |
|||||||||||||
|
|
|
|
|
|
|
|||||||
I |
|
I |
|
|
I |
|
|
|
j1 . 76 |
0 . 89 |
|||
L1 |
L2 |
L0 |
j(0 . 6 1 . 385) |
||||||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||
и модуль тока включившейся фазы А по месту несимметрии
I |
2 |
3I L1 |
3 0.89 2.67 . |
|
LA |
||||
|
|
|
Симметричные составляющие тока прямой и обратной последовательностей в цепи генератора, с учетом перехода через трансформатор, составят:
I |
Г1 |
I |
e |
j30 |
11 |
0.89e |
j30 |
, |
|
|
|
||||||
|
|
L1 |
|
|
|
|
|
I |
Г2 |
I |
e |
j30 |
11 |
0.89e |
j30 |
. |
|
|
|
||||||
|
|
L2 |
|
|
|
|
|
Наибольшей величины токи в цепи генератора достигают в фазах А и С, которые равны по модулю:
I |
2 |
I |
2 |
0. 89e j30 0. 89e j30 1. 54 ; |
|
Г A |
|
Г C |
|
ток фазы В равен нулю.
Искомые соотношения между наибольшими сверхпереходными токами при различных условиях включения составляют:
в цепи генератора
IГ3 : IГ1 : IГ2 2.93: 2.86 :1.54 1: 0.98: 0.53;
в линии L
I L3 : I L1 : I L2 2.93: 2.79 : 2.67 1: 0.95: 0.91.
83

ПРИМЕР 3.2. Однократная продольная несимметрия и комплексная схема замещения
Для схемы рис. 8.9, а при обрыве одной фазы вначале линии:
–определить токи неповрежденных фаз;
–построить эпюры распределения симметричных составляющих напряжений;
–рассчитать фазные напряжения в месте разрыва линии.
Исходные данные. Комплексная схема для рассматриваемого режима приведена на рис. 3.2, б, где все параметры выражены в относительных единицах при базисных условиях.
е
е
е
Рис. 3.2. К примеру 3.2: а – исходная схема; б – комплексная схема замещения
Решение
1. Результирующие реактивности схем прямой, обратной и нулевой последовательностей относительно места разрыва составляют:
xL1Σ 0.15 0.2 1.2 0.25 0.2 2.0 ;
xL2Σ 0.15 0.2 0.35 0.25 0.2 1.15 ;
xL0Σ 0.57 0.2 0.2 0.97
84
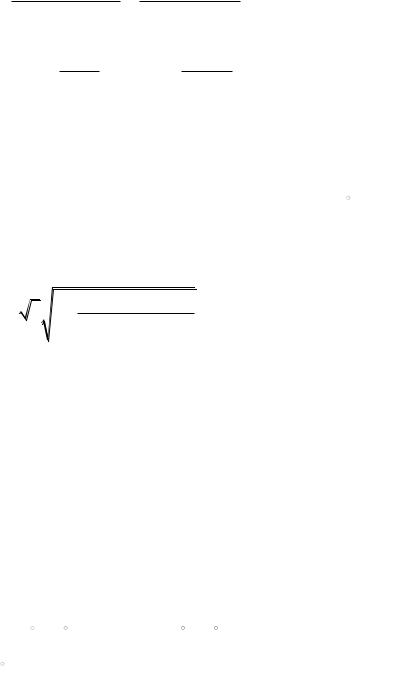
и дополнительная реактивность
|
|
|
|
|
|
|
|
x |
1 |
x |
L2 |
|
// x |
L |
|
L |
|||||||
|
|
|
2. Расчет токов схемы Определим симметричные
ных последовательностей:
0Σ 1.15// 0.97 0.526 .
составляющие токов в схемах отдель-
I |
L a1 |
|
|
|
I |
L a2 |
|
|
|
I L0 0
|
|
E |
|
|
|
|
|
|
j1. 43 |
|
|
||||
|
|
|
|
|
1 |
|
|
|
|
|
|
0. 565 |
; |
||
|
|
|
|
|
|
|
|
|
|
j(2 0. 526) |
|
||||
j(x |
|
|
|
x |
1 |
) |
|
|
|||||||
L1Σ |
L |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
1 |
|
|
|
|
|
0. 526 |
|
|
|
I |
|
|
|
|
L |
0. 565 |
0. 258 |
||||||||
L a1 |
x |
|
1. 15 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
L2Σ |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
. 565 |
0. 526 |
0. 307 , |
|
|
|||||||||||
|
0. 97 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
;
что позволяет рассчитать ток в неповрежденных фазах линии:
I |
LB |
I |
LC |
a |
2 |
0.565 |
a 0.258 0. 307 |
0. 85e |
j237 |
. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
Модуль этих токов можно определить и по выражению (8.18), ис-
пользуя коэффициент
m |
1, 1 |
|
m |
1, 1 |
|
|
|
3 |
, т. е.
1 |
1. 15 0. 97 |
|
|
(1. 15 0. 97) |
2 |
||
|
|||
|
|
0. 565
0.
85
.
3. Расчет напряжений в узлах схемы |
|
|
|
Найдем симметричные составляющие напряжения на клемме |
, |
||
L |
учитывая, что в узле е схем отдельных последовательностей напряжения равны нулю:
U |
L a1 |
I |
La1 |
j(x |
3 |
|
|
|
U L a2 I La2 j(x3
U L 0 I L0 j(x3
x4 x5) 0.565 j(0.15 0.2 1.2) j0.876;
x4 x5) 0.258 j(0.15 0.2 0.35) j0.18; x4 ) 0.307 j(0.57 0.2) j0.236 .
На базе найденных значений симметричных составляющих напряжений определяем фазные напряжения в узле L :
U |
L A |
j(0.876 0.18 0.236) |
|
|
j0.46
;
U L B 0 . 876e j 240 90 0 . 18e j 120 90 0 . 236e j901 . 085e j32. 56 ;
85
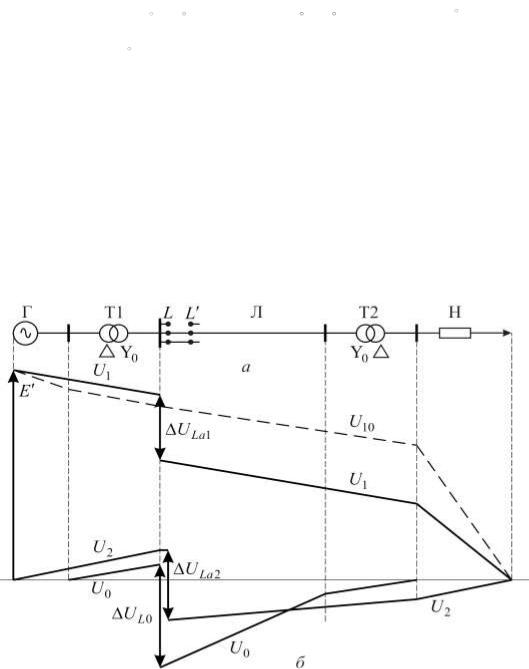
U |
|
|
|
0 . 8 7 6e |
j |
|
|
90 |
|
0 . 1 8e |
j |
2 40 90 |
|
0 . 2 3 6e |
j9 0 |
|
|||||||||||
L C |
|
1 2 0 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 . 0 8 5e |
j14 7 . 4 4 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Рассчитаем симметричные составляющие падения напряжения в |
|||||||||||||||||||||||||||
месте разрыва: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
U |
La1 |
U |
La2 |
U |
L0 |
I |
La1 |
jx |
|
1 |
|
0.565 j0.526 j0.297 |
|||||||||||||||
|
L |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
и симметричные составляющие напряжения на клемме L: |
|
|
|||||||||||||||||||||||||
U |
La1 |
U |
L a1 |
U |
La1 |
j(0.876 0.297) j1.173; |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
U La2 U L a2 U La2 |
j( 0.18 0.297) j0.117; |
|
|||||||||||||||||||||||||
U |
L0 |
U |
L 0 |
U |
L0 |
|
|
|
j( 0.236 0.297)
j0.
061
.
Рис. 3.3. К примеру 3.2: а – принципиальная схема; б – эпюры напряжений при разрыве одной фазы
Напряжение фазы А на стороне L через симметричные составляющие определится так:
U LA j(1.173 0.117 0.061) j1.351,
или через вектор падения напряжения в месте разрыва
U LA U L A U LA j(0.46 3 0.297) j1.351.
86
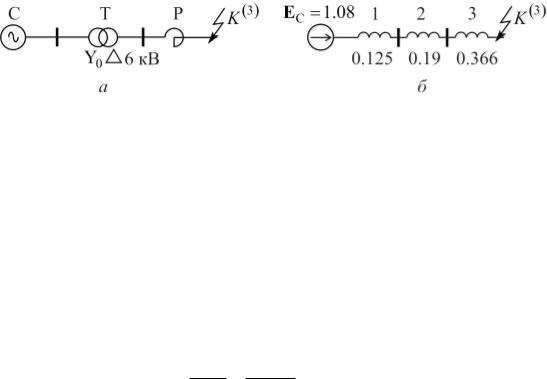
Для неповрежденных фаз В и С фазные напряжения со стороны клеммы L и L одинаковы. Эпюры напряжений отдельных последовательностей приведены на рис. 3.3, б.
Пунктиром показано распределение напряжения в нормальном режиме. В месте разрыва напряжения обратной и нулевой последовательностей меняют свой знак. Векторные диаграммы напряжений в месте разрыва представлены на рис. 3.3.
емой
ПРИМЕР 3.3.
EС = const. За
Схема (рис. 3.4, а) питается системой, характеризулинейным реактором на стороне 6 кВ происходит
трехфазное короткое замыкание. Определить значения токов КЗ для следующих условий: наличие реактора; отсутствие реактора; одна из фаз реактора закорочена.
Рис. 3.4. К примеру 3.3: а – принципиальная схема; б – схема замещения прямой последовательности
Исходные данные. Параметры схемы прямой и обратной последовательностей одинаковы и представлены на рис. 3.4, б в относительных единицах при принятых базисных условиях ( I б = 9.16 кА на ступе-
ни 6 кВ).
Решение
1. При наличии реактора
x |
0.125 0.19 0.366 0.681 |
1 |
|
и значение тока трехфазного КЗ в относительных единицах
I |
3 |
|
jEc |
|
1. 08 |
1. 59 |
|
K |
jx |
0. 681 |
|||||
|
|
|
|
||||
|
|
|
|
|
|||
|
|
|
1 |
|
|
|
и в именованных – I |
3 1. 59 9. 16 14. 6 |
кА. |
|
|
K |
|
|
2. При отсутствии реактора в схеме |
|
||
x |
|
0.125 0.19 0.315 |
|
1 |
|
|
|
и значение тока трехфазного КЗ в именованных единицах
I |
3 |
jEC |
I |
б |
|
1. 08 |
9. 16 31. 4 кА. |
|
|
||||||
|
K |
jx1 |
|
0. 315 |
|
||
|
|
|
|
|
|||
87

3. При условии закорачивания одной фазы реактора Закорачивание фазы реактора эквивалентно включению в эту фазу
реактивности x = – 0.366, при условии наличия реактора во всех трех
фазах. Расчетные выражения заимствуем из [1, табл. 8.1] для несимметрии L(1).
Учитывая, что результирующая реактивность нулевой последовательности равна бесконечности ( x0 ), дополнительная реактив-
ность, включаемая в схему прямой последовательности, будет составлять
|
|
x |
3 |
|
|
|
|
|
|
0. 366 |
|
|
|
x |
1 |
|
|
|
// x |
2 |
|
|
|
|
|
// 0. 681 0 . 149. |
|
L |
|
|
|
||||||||||
|
|
3 |
|
|
|
|
|
3 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
Находим симметричные составляющие токов фазы А:
I |
|
|
E |
|
|
|
L a1 |
|
1 |
1 |
|||
|
j(x |
|
x |
) |
||
|
|
|
L |
|||
|
|
1 |
|
|
||
j1 . 08 j(0 . 681 0 . 149)
2 .
03
;
ILa2
|
|
|
x 1 |
L |
|
|
x |
|
2 |
ILa1
|
( 0.149) |
2.03 |
|
|
0.681 |
||||
|
|
|
0.444
.
Наибольший ток будет в фазе А (в которой условно отсутствует реактор):
I |
L |
(I |
La1 |
I |
La2 |
)I |
б |
(2.03 0.444) 9.16 22.66 |
|
|
|
|
|
кА;
токи в фазах В и С составляют около 17 кА.
Таким образом, закорачивание одной фазы реактора при заданных условиях приводит к увеличению тока короткого замыкания в 1.55 раза.
4. ЗАМЫКАНИЯ В СЕТЯХ С ИЗОЛИРОВАННОЙ НЕЙТРАЛЬЮ И ЭЛЕКТРОУСТАНОВКАХ ДО 1 КВ
ПРИМЕР 4.1. Однофазное короткое замыкание
Определить ток при простом металлическом замыкании на землю в сети 37 кВ, имеющей воздушные линии (ВЛ) общей протяженностью
200 км.
ВЛ: провод марки АС-95; расположение проводов по вершинам
треугольника с расстояниями (м) |
d AB |
= 4.06, |
d AC = 3.5, |
d BC |
= 3.09; |
|||||
высота подвеса проводов |
h |
A |
h |
8, |
h |
B |
11. |
|
|
|
|
|
C |
|
|
|
|
|
|
||
При заданных параметрах линии (радиус провода r = 6.75 10-3 м) находим:
– среднее геометрическое расстояние между проводами:
88

D |
ср |
3 |
4.06 3.5 3.09 3.53 |
|
|
|
м;
– средний геометрический радиус системы трех проводов:
Rcp |
3 |
6. 75 |
10 |
3 |
3. 53 |
2 |
0. 44 |
м; |
|
|
|
– среднее расстояние проводов А, В и С до их зеркальных отражений относительно земли:
Di 2 |
8 11 8 |
18 |
м; |
|
3 |
||||
|
|
|
– емкостное сопротивление 1 км линии:
xC0 |
396 |
|
18 |
|
10 |
3 |
636 10 |
3 |
Ом; |
lg |
0. 44 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
– и соответственно всей сети:
x |
|
|
636 |
10 |
3 |
3180 |
C0Σ |
|
|||||
200 |
|
|||||
|
|
|
|
|
||
|
|
|
|
|
|
Ом.
Искомый ток замыкания на землю по выражению (9.1) составляет
I |
|
3 |
37000 |
|
|
з |
3( j3180) |
||||
|
|
|
|||
|
|
|
|
j20
А
и по приближенному выражению
IU ср.ном
зN
L |
37 200 |
|
350 |
||
|
21
А.
В данном случае для полной компенсации тока замыкания на землю необходимо в нейтраль обмотки 37 кВ трансформатора включить катушку с индуктивным сопротивлением
x |
|
|
3180 |
1060 |
|
L |
3 |
||||
|
|
|
|||
|
|
|
|
Ом.
ПРИМЕР 4.2. Короткие замыкания в сети 0,4 кВ
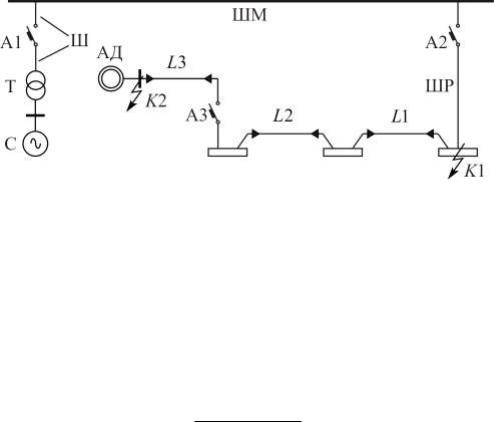
Для схемы, представленной на рис. 4.1, определить наибольшие и наименьшие значения токов при коротких замыканиях поочередно в точках K1 и K2.
Исходные данные
Трансформатор Т: 1000 кВА, |
10/0.4 кВ, |
Y/Y0 – 12. |
Шины Ш: 3.5 м, А-2(80 8), |
расстояние между фазами –200 мм. |
|
Шинопровод магистральный |
ШМ: 50 м, |
I ном 1600А. |
89
Шинопровод распределительный ШР: 4 м, |
I ном 600А. |
|||
Кабели: |
L1 = 10 м, |
А(3 50+1 25); |
L2 = 8 м, А(3 35+1 16); |
|
L3 = 11 м, |
А(3 16+1 10); все кабели с алюминиевой оболочкой. |
|||
Автоматы: А1 – 1500 А; |
А2 – 600 А; А3 – 50 А. |
|||
Рис. 4.1. Схема к примеру 4.2
Решение. Используя справочный материал [1,2; приложение табл. П3, П4, П6], находим сопротивления элементов заданной схемы:
для трансформатора Т
r1 |
=1.7 мОм, |
x1 |
= 8.6 мОм, |
r0 |
= 0.9 мОм, |
x0 |
= 80 мОм; |
для шины Ш
x1
