Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Политехнический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

RGR_1

.pdf

Скачиваний:

Добавлен:

29.05.2015

Размер:

726.41 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

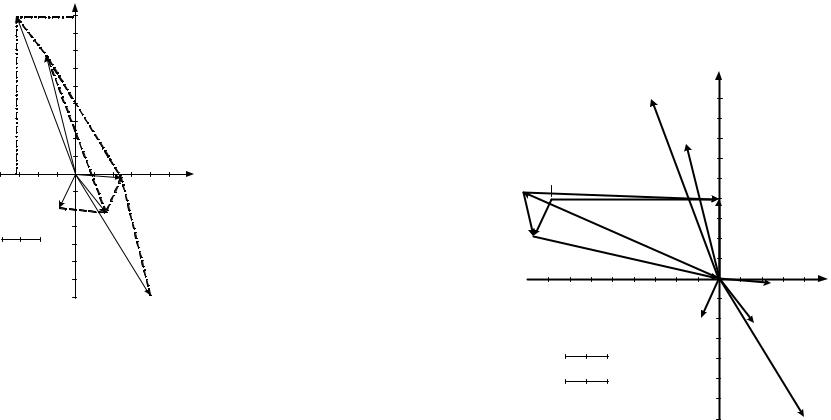
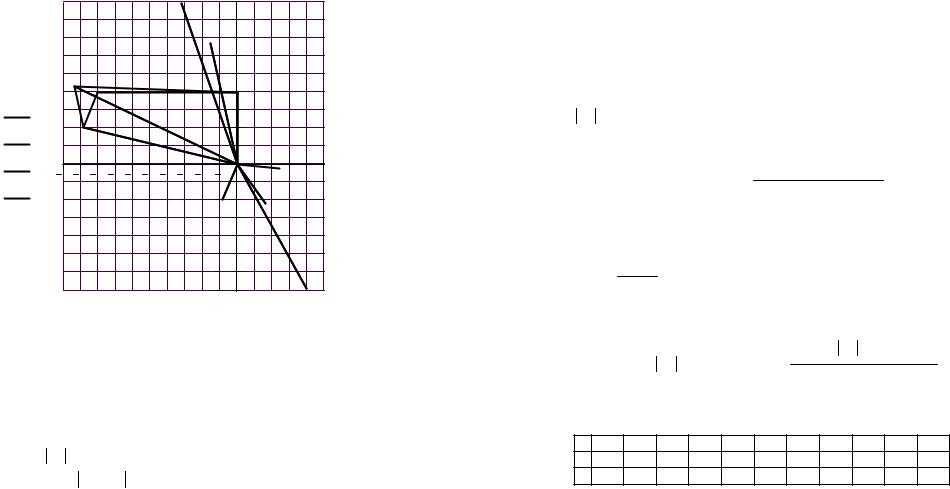
имеем I&5 = I&4 + J& , т.е. I&5			является диагональю параллелограмма, обра-
зованного токами I&4 и J& .
			+j
			2.223
		I&
		1
			I&4
		-0.795	0			+1
		-0.795	&	I&5		+1
			I2
				I&3
				J&
Для упрощения построения топографической диаграммы напряже-
ний	на	комплексной	схеме	расставляем		стрелки	напряжений
U&2 ,U&3 ,U&4 ,U&5 навстречу направлениям токов. Далее, используя закон
Ома и учитывая наличие индуктивной связи, проводим расчет этих
напряжений (встречное включение):
U&2	= Z 2 I&2 = −20.5 − j49.3 = 53.39e− j112.6o				В;
U&3 = Z 3I&3 −Z M I&4 = 220.4 − j50.65 = 226.14e− j12.9o В;
U&4 = Z 4 I&4 −Z M I&3 = −233.2 + j107.7 = 256.9e− j155.21o В;
U&5 = Z 5 I&5 =12.81− j57.03 = 58.45e− j77.3o					В;
E&	= j100 =100e j90o В;
1
E&	=100 = 200e j0o В;
2
U&J	= 233.3 − j7.7 = 233.4e− j1.9o			В.
				41

	Затем рассчитываем комплексные потенциалы узлов и точки k
схемы, предварительно приняв, например,							ϕb = 0 :
&	&	&		= −233.2		+ j107.7 В;
ϕa	= ϕb +U4			= −233.2		+ j107.7 В;
&	&	&		= j100 В;
ϕd	= ϕb + E1			= j100 В;
&	&	&		= −220.4		+ j50.65 В;
ϕc	= ϕb −U3			= −220.4		+ j50.65 В;
&	&	&		= −199.9		+ j99.95 В.
ϕk	= ϕc −U2			= −199.9		+ j99.95 В.
							+j
						I1
				k		I4
		a		k		U J
		a				U J
						E2	d
		5	U2		U4	E2	E
			U2				E
							1
		c			U3
					U3
						-	b
						-	0	I5	+1
							0
						I2
						I2
								I3
					50 В
					0,5 А
									J
Принимаем масштаб векторов напряжений и потенциалов узлов,
например,		mU = 50 В/см. На комплексной плоскости, где уже построе-
ны векторы токов, отмечаем точками потенциалы узлов и точки k, от-
кладывая их вещественные и мнимые составляющие по вещественной
и мнимой осям соответственно, в принятом масштабе mU . Далее со-
единяем точки потенциалов векторами напряжений согласно их на-
правлениям на комплексной схеме замещения.

6. Определяем показание вольтметра аналитически и графически, как действующее значение напряжения, между точками включения вольтметра, т.е. между узлами a и d.

−Аналитически:

UV =	&	= 233.425 В или UV =	ϕd −ϕa	=	233.2 − j7.7	= 233.425 В.
	&
	UJ
			& &

− uurГрафически (по векторной диаграмме):

UV = ad mV = 4.65 50 = 232.5 В.

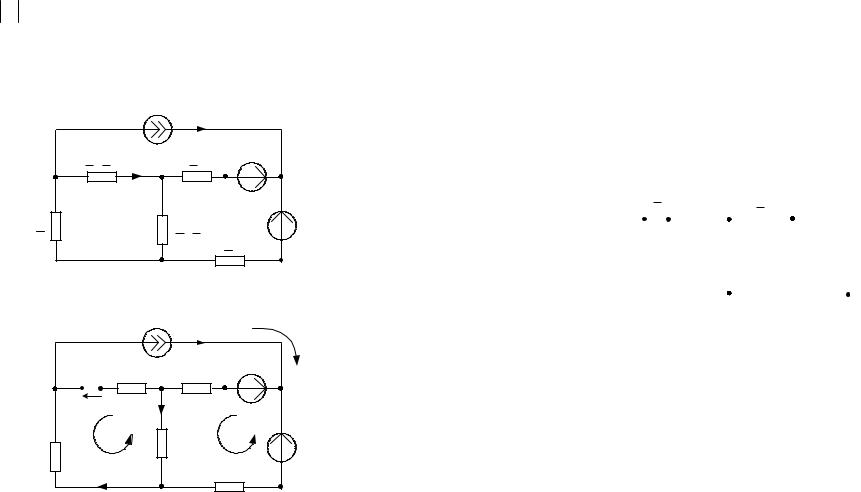
7. Делаем развязку индуктивной связи и методом эквивалентного генератора находим ток ветви ab, т.е. I&ab = I&4 . При развязке учитываем, что индуктивно связанные сопротивления Z 3 и Z 4 подходят к общему узлу b одинаковым образом.

Далее относительно сопротивления R бывшей ветви ab (после развязки ветвь am) используем метод эквивалентного генератора.

			J		I11
a		j(X4-XM)m	ZM	b	d
					d
	&	&( xx)			E
	EÃ	I	3		1
		(Z3-ZM)			I22
Z5		(Z3-ZM)
Z5	I&5( xx)			Z2	E2
	I&5( xx)			Z2	k
		c			k
		c

Для определения токов

&(xx)

во вспомогательной схеме приме-

ним метод контурных токов:

I11

= J

− E& ,

− Z

+ Z

)− I&

= E&

− E&

+ J& Z

тогда I&22 =

= 0.627

− j1.119 А. В результате:

Z 2 + Z 3

&(xx)

0.627 − j1.119 А;

&(xx)

= I

= J =1− j1.73 А.

Затем по 2 закону Кирхгофа составляем уравнение и находим E&Г :

E&Г = −(Z 3 −Z M )I&3(xx) −Z 5 I&5(xx)

= −55.65 + j334.35 =338.95e j99.45o В, т.е.

EГ =338.95 В, αГ =99.45o .

Во вспомогательной схеме ветвь с источником тока разрываем,

ЭДС

закорачиваем и относительно зажимов сопротивления

R ветви ab находим Z Г :

}

Z Г =Z 5 + j (X 4

− X M )+ (Z 3 −Z M )(Z 2 +Z M ) =97.5− j12.5 =

Z 3 −Z M +Z 2 +Z M

=98.3e− j7.3o

Ом,

т.е. RГ =97.5 Ом;

X Г =−12.5 Ом; ϕГ =−7.3o ;

ZГ =98.3 Ом.

Далее находим ток ветви ab:

I&4 =

E&Г

=−0.387 + j1.668 =1.713e j103o

А,

Z Г +R

который совпал со значениями, найденными при помощи законов Кирхгофа и метода контурных токов.

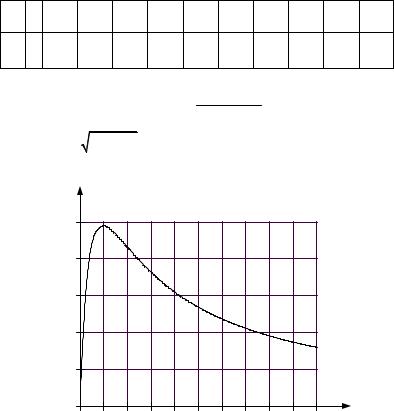
Затем изменяя величину	сопротивления		R ветви ab от 0 до
10ZГ =983 Ом рассчитываем мощность Pab ,			которая выделяется в
виде тепла в этом сопротивлении:
Pab =	EГ2 R
		.
	(R +RГ )2 + X Г2

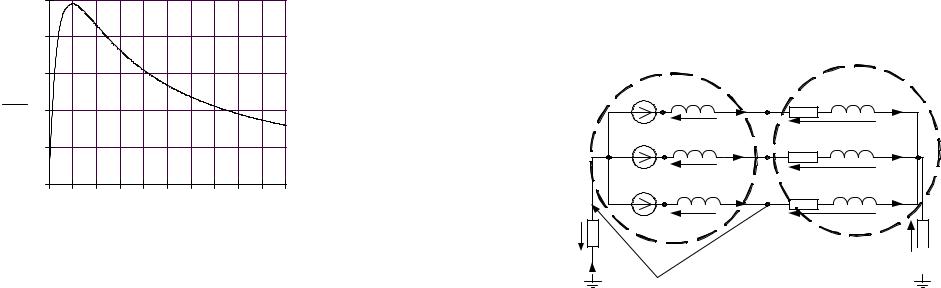
Результаты расчетов этой мощности вносим в таблицу:

98.3

196.6 294.9 393.2 491.5 589.8 688.1 786.4 884.7

983

Ом

Pab ,

293.4 260.7 219.8 187.5 162.7 143.4 128.1 115.6 105.3

96.7

Вт

Максимум

мощности

EГ2

) =293.4

Вт

наблюдается

Pab = Pm = 2(R +R

при

R = R

R2 + X

= Z

=98.3 Ом.

Строим график зависимости

P = f (R) .

Pab(R)

Вт

300

240

180

120

100 200 300 400 500 600 700 800 900 1000

R, Ом

8. Необходимо сформулировать вывод по выполненным пунктам

задания, в котором сравнить результаты вычислений, оценить трудо-

емкость методов расчета и проанализировать график мощности п.7.

Расчет РГР №2 при помощи программы MathCad осуществляется следующим образом:

Дано:

ORIGIN:= 1

E1 := 100

e90 degi

J := 2 e− 60 degi

L := 318.47 10− 3

E2 := 200

e0 degi

ω := 314

C := 31.8 10− 6

E3 := 0

R := 100

M := L

Расчет комплексных сопротивлений :

ZL := i ω L

ZC := −i

ZM :=

ω C

ZL = 100i

ZC = −100.148i

ZM = 50i

Z1 := 0

Z2 := R

Z3 := 2

R + ZL

Z4 := R + ZL

Z1 = 0

Z2 = 100

Z3 = 200 + 100i

Z4 = 100 + 100i

Z5 :=

Z5 = 30.08 − 90.107i

3R + ZC

1. Метод законов Кирхгофа

0 0

−1

−J

−1

0 1

−1

1 0

A :=

B :=

−ZM

−E1 + E2

Z3 − ZM

Z4 − ZM

0 0

−ZM

0 1

1.1. Решение матричного уравнения:

X := A− 1

−0.795 + 2.224i

−0.205 − 0.492i

I1 := X1

I2 := X2

0.408 − 0.555i

I3 := X3

I4 := X4

−0.387 + 1.67i

I5 := X5

UJ := X6

0.613 − 0.062i

233.372− 7.911i

1.2.Значения токов и напряжения на источнике тока

валгебраической форме записи:

I1 = −0.795 + 2.224i

I2 = −0.205 − 0.492i

I3 = 0.408 − 0.555i

I4 = −0.387 + 1.67i

I5 = 0.613 − 0.062i

UJ = 233.372− 7.911i

1.3. Определение модулей и фаз токов и напряжения:

I1	= 2.362		arg(I1) = 109.66deg
I2	= 0.533		arg(I2)	= −112.644deg

I3	= 0.688		arg(I3)	= −53.658deg

I4	= 1.714		arg(I4)	= 103.039deg

I5	= 0.616		arg(I5)	= −5.797deg

UJ		= 233.506	arg(UJ) = −1.942deg

2.Метод контурных токов

2.1.Определение значений контурных токов и напряжения на источнике тока:

J33 := J

		Z2 + Z3	−(Z2 + ZM)	0
A1	:= −(Z2 + ZM)		Z2 + Z4 + Z5	0

		−Z2	Z2 + Z5	−1
		−E1 + E2 + J33 Z2
B1	:= E1 − E2 − J33 (Z2 + Z5)

		−E2 − J33	(Z2 + Z5)

X1 := A1− 1 B1

		0.408 − 0.555i		J11	:= X11
X1	=	−0.387	+ 1.67i	J22	:= X1
			− 7.911i		2
	233.372		− 7.911i	UJk := X1
					3

2.2.Значения контурных токов и напряжения на источнике тока в алгебраической форме записи:

J11 = 0.408 − 0.555i

J22 = −0.387 + 1.67i UJk = 233.372− 7.911i

2.3. Определение токов в ветвях:

I1k := J22 − J11			I1k = −0.795	+ 2.224i
I2k := J11	− J22	− J33	I2k = −0.205	− 0.492i
I3k := J11			I3k = 0.408 − 0.555i
I4k := J22			I4k = −0.387	+ 1.67i
I5k := J22	+ J33		I5k = 0.613 − 0.062i

2.3.Расчитываем напряжения на пассивных элементах с учетом наличия индуктивной связи:

U2 := Z2	I2	U2	= −20.535− 49.226i
U3 := Z3	I3 − ZM I4	U3	= 220.535− 50.774i
U4 := Z4	I4 − ZM I3	U4	= −233.372+ 107.911i
U5 := Z5	I5	U5	= 12.837− 57.137i

или

U2	= 53.337	arg(U2)	= −112.644deg
U3	= 226.304	arg(U3)	= −12.965deg

U4	= 257.114	arg(U4)	= 155.184deg

U5	= 58.561	arg(U5)	= −77.337deg

3.Баланс мощности

3.1.полная мощность

S := E1 I1 + E2 I2 + UJ J S = 428.436+ 415.287i

3.2. активная мощность

P := (

Re(Z1) + (

)2 Re(Z2) + (

)2 Re(Z3) ...

+ (

)2 Re(Z4) +

(

)2 Re(Z5)

P = 428.436

3.3. реактивная мощность

:= (

Im(Z1) + (

)2 Im(Z2) + (

)2 Im(Z3) ...

+ (

)2 Im(Z4) +

(

)2 Im(Z5)

:= 2

cos (arg(I3) − arg(I4)) Im(ZM)

Q := Q1 − Q2

Q = 415.287

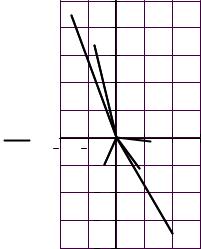
4.Лучевая диаграмма токов и топографическая диаграмма напряжений

4.1.лучевая диаграмма токов

m := 20 - коэффициент для масштаба тока

I := ( 0 J 0 I1 0 I2 0 I3 0 I4 0 I5) m

20 Im(IT) 10

20 10 0 10 20 30

Re(IT)

4.2. Топографическая диаграмма напряжений (строится совмещенно с лучевой диаграммой токов)

n := 0.2 - коэффициент для масштаба напряжения

4.2.1. Контур bacb:

ϕb := 0
ϕa := ϕb + I4	Z4 − I3 ZM
ϕc := ϕa + I5 Z5
ϕbb := ϕc + I3	Z3 − I4 ZM потенциал ϕbb должен быть

равен ϕb

ϕb					0
	ϕa				−46.674+ 21.582i
			ϕ1	=
ϕ1 :=	ϕc	n
					−44.107+ 10.155i
					0 − 0i
ϕbb
4.2.2. Контур bdkcb:
ϕd := ϕb + E1
ϕk := ϕd − E2
ϕcc := ϕk + I2 Z2				потенциал ϕсс должен быть равен ϕс

ϕbb := ϕcc + I3 Z3 − I4 ZM потенциал ϕbb должен быть равен ϕb

ϕb				0
	ϕd			20i
	ϕd			20i
ϕ2 :=	ϕk	n	ϕ2 =	−40 +	20i
	ϕcc			−44.107+
	ϕcc			−44.107+	10.155i
ϕbb				−0

4.2.3. Контур bdab:

ϕaa := ϕd − UJ потенциал ϕaa должен быть равен ϕa

ϕb

6. Определяем ток в ветви ab методом эквивалентного

ϕd

20i

генератора

ϕ3 :=

ϕ3 =

6.1. По методу контурных токов определяем токи ХХ

ϕaa

−46.674+ 21.582i

ϕb

J11 := J

J11 = 1 − 1.732i

J22 :=

E2 − E1 + J Z2

J22 = 0.627 − 1.12i

Z2 + Z3

I3xx:= J22

I5xx:= J11

6.2. ЭДС генератора

Im(IT)

Eg := −(Z3 − ZM) I3xx− Z5 I5xx

Eg = −55.351+ 334.79i

= 339.335

arg(Eg) = 99.388deg

Im(ϕ1)

6.3. Сопротивление генератора

Im(ϕ2)

(Z3 − ZM) (Z2 + ZM)

Im(ϕ3)

50 45 40 35 30 25 20 15 10 55 0

5 10 15 20 25

Zg := Z5 + Im(Z4 − ZM) i +

Z3 + Z2

Zg = 97.58 − 12.607i

6.4. Определяем ток в ветви ab

I4 := Zg + R

I4 = −0.387 + 1.67i

Re(IT),Re(ϕ1) ,Re(ϕ2) ,Re(ϕ3)

7. Расчитываем мощность Pab

(

Eg )2

Построенные диаграммы рекомендуется скопировать в

i := 1..11

Rri :=

(i − 1)

Pabi

графический редактор, например,

Microsoft Visio и проставить

(Rri + Re(Zg))

+ Im(Zg)

индексы узлов и направления стрелок векторов токов и

напряжений.

T := stack(RrT ,PabT)

5. Определяем показания вольтметра

Uv :=

Uv = 233.506

0.0

98.4 196.8 295.2 393.6 492.0 590.3 688.7 787.1 885.5 983.9

или

Uv :=

ϕd − ϕa

Uv = 233.506

0.0

293.8 261.0 220.1 187.7 162.9 143.6 128.2 115.8 105.5

96.9

7.1. Построение зависимости Pab(R)
		R					(	Eg	)2 Rr
							(	Eg	)2 Rr
i := 1..31 Rr	:=		(i − 1)	Pab		:=			i
i := 1..31 Rr	:=		(i − 1)	Pab		:=
i		3			i		(Rri + Re(Zg))2 + Im(Zg)2

P(r) := interp(cspline(Rr,Pab) ,Rr,Pab ,r)

300
240
180
P(r)
120
60
0	100	200	300 400	500	600 700	800	900 1000
				r

Методические указания к заданию № 3 (5).

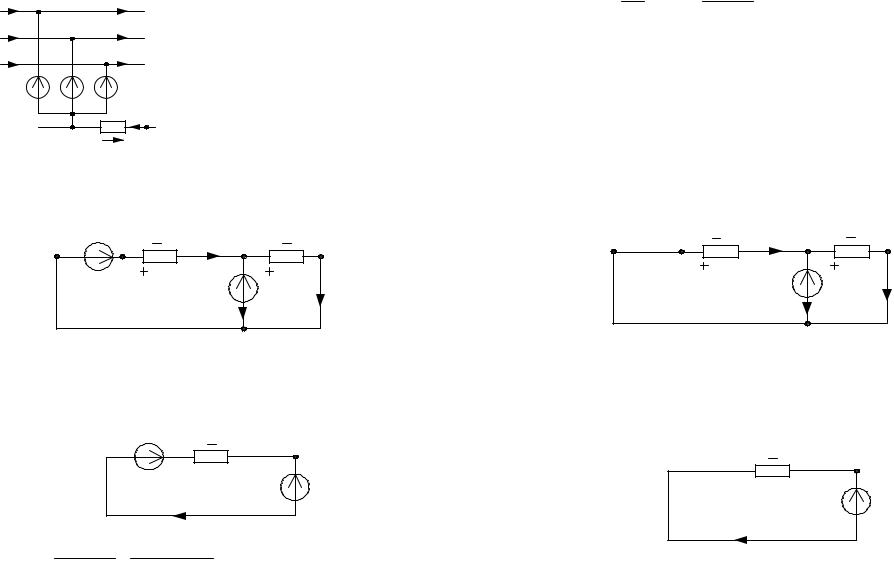
Для заданной схемы дано:

E&A = 220 e− j90o B;

E&B = a2 EA ; E&C = a EA ;

X Г1 = X Дв1 = 20 Oм;

X Г2 = X Дв2 =10 Oм;

X Г0 = X Дв0 = 5 Oм;

R = 20 Oм;

Zn = − j5Oм; ZN = ∞.

Генератор Двигатель

.	I.ГA a		jxДв1,2,0 I.ДвA
EA A jxГ1,2,0		R

UN ZN

I.N

.		.					.
.		UГA	I.ГB				UДвA	I.ДвB
EB B		jxГ1,2,0	I.ГB	b	R	jx	Дв1,2,0	I.ДвB	n
.		.					.
.		UГB	I.			jx	UДвB	I.
EC	C	jxГ1,2,0	I.	c	R	jx	Дв1,2,0	I.
	C		ГC	c			.	ДвC
		.					.	.
		U				UДвC		.	Zn
		ГC						Un	Zn
		ГC

I.n

1. Короткое замыкание фазы С на нейтраль N генератора.

Для особой фазы С рассчитываем симметричные составляющие напряжений и токов.

1.1. В место повреждения вводим фиктивные ЭДС U&A , U&B , U&C и записываем условие: I&A = 0; I&B = 0; U&C = 0 .

I.ГA	a		I.ДвA
I.ГB		b	I.ДвB
I.ГC		c	I.ДвC

.	.	.
UA	UB	UC	ZN	I.
				N
	k		.	m
			UN

В результате:

I&С = I&С1 + I&С2 + I&С0 ;

+ a

2 &

I&С1 = a

I А

+aIВ

IС

I&С =

IС

;

I&С2 = a2

А + aI

IС

I&С

IС

;

I&С0 =

I&А + I&В + I&С

I&С

где

a = e j120o ; a2 = e− j120o ; a3 = e j360o =1.

1.2. Расчётная схема прямой последовательности для особой фазы С:

где Z Г1 = jX Г1 = j20 Ом; Z Дв1 = R + jX Дв1 = 20 + j20 Ом.

Складываем параллельные ветви с Z Г1 и Z Дв1 , получаем эквивалентную схему:

ECЭ

I.C1

UC1

где

Z Г1

Z Дв1

j20 (20

+ j20)

= 4

+ j12 =

12e

j71.56o

Ом

Z Г1

+ Z Дв1

j20 +20 + j20

– эквивалентное сопротивление прямой последовательности;

j30 12e j71.56o

j11.56o

= 220e

=136 + j27.885

=139.15e

= E

CЭ

C Z Г1

j20

– эквивалентная ЭДС фазы С.

В результате на основании законов Ома и Кирхгофа можно за-

писать расчётные формулы:

С1

= E&

−Z

; U&

ДвC1

=U&

С1

; I&

ДвC1

=U&

ДвC1

/ Z

Дв1

;

CЭ

I&ГC1 = I&C1 + I&ДвC1; U&ГC1 = Z Г1I&ГC1.

Расчёт по этим формулам будет возможен после определения

составляющей тока короткого замыкания прямой последовательности

фазы С, т.е. I&C1 .

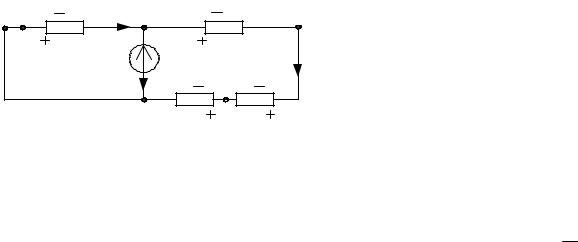
1.3. Расчётная схема обратной последовательности для особой фа-

зы С:

I.ГC2 c

ZГ2

Z Дв2

UГC2

UДвC2

UC2

I ДвC2

IC2

где

Z Г2 = jX Г2 = j10 Ом;

Z Дв2 = R + jX Дв2 = 20 + j10 Ом.

Складываем параллельные ветви с Z Г2

и Z Дв2 ,

получаем эк-

вивалентную схему:

Z 2	=	Z Г2	Z Дв2	=	j10 (20 + j10)	= 2.5	+ j7.5	= 7.906e	j71.56o	Ом;
		Z Г2	+ Z Дв2		j10 +20 + j10

– эквивалентное сопротивление обратной последовательности.

В результате на основании законов Ома и Кирхгофа можно записать расчётные формулы:

U&С2 = −Z 2 I&C 2 ; U&ДвC 2 =U&С2 ; I&ДвC 2 = U&ДвC 2 / Z Дв2 ; I&ГC 2 = I&C 2 + I&ДвC 2 ; U&ГC 2 = Z Г2 I&ГC 2.

Расчёт по этим формулам будет возможен после определения составляющей тока короткого замыкания обратной последовательности фазы С, т.е. I&C 2 .

1.4. Расчётная схема нулевой последовательности для особой фазы С:

где

Z 0	=	Z Г0 (Z ДВ0 +3Z N +3Z n )		=	j5 (20 + j5 +∞− j15)			= Z Г0	= j5 Ом –
		Z Г0	+ Z ДВ0 +3Z N +3Z n		j5	+20	+ j5 +∞− j15

эквивалентное сопротивление нулевой последовательности.

В результате на основании законов Ома и Кирхгофа можно записать расчётные формулы:

U&С0 = −Z 0 I&C0 ;	I&ДвC0	=		U&С0	; U&ДвC0	=I&ДвC0 Z Дв0 = 0;
			Z ДВ0	+3Z N +3Z n

U&n = 3Z n I&ДвC0 = 0; U&N = 3Z N I&ДвC0 =U&С0 ; I&ГC0 = I&C0 + I&ДвC0 ;

U&ГC0 = Z Г0 I&ГC0 = −U&С0 .

Расчёт по этим формулам будет возможен после определения составляющей тока короткого замыкания обратной последовательности фазы С, т.е. I&C0 .

Рассчитываем симметричные составляющие напряжений и токов особой фазы С.

Так как U&С =U&С1 +U&С2 +U&С0 = (E&CЭ −Z1I&C1) +(−Z 2 I&C 2 ) +(−Z 0 I&C0 ) = 0

и I&С = I&С1 + I&С2 + I&С0

I&С

, то

I&С =

3E&

= 3

139.15e j11.56o

CЭ

Z1 + Z 2 + Z 0

(4 + j12) +(2.5 + j7.5) + j5

= 7.328 − j14.749 =16.47e− j63.58o A.

В результате по вышеприведённым формулам находим симметричные составляющие прямой последовательности напряжений и токов фазы С:

I&С1		=	I&С		= 2.443 − j4.916 A;
I&С1		=	3		= 2.443 − j4.916 A;
			3
U&	С1	= E&				− Z	1	I&	=136.327 + j27.885 −(4 + j12)(2.443 − j4.916) =
	С1		CЭ				1	C1
									= 67563 + j18.233 B;
U&ДвC1 =U&С1 = 67563 + j18.233 B;
I&ДвC1			=	U&		ДвC1		= 2.145 − j1.233 A;
I&ДвC1			=		Z Дв1			= 2.145 − j1.233 A;
					Z Дв1

I&ГC1 = I&C1 + I&ДвC1 = (2.443 − j4.916) +(2.145 − j1.233) = 4.588 − j6.149 A;

U&ГC1 = Z Г1I&ГC1 = j20 (4.588 − j6.149) =122.98 + j91.76 B.

Далее находим симметричные составляющие обратной последовательности напряжений и токов фазы С:

I&С2 = I&3С = 2.443 − j4.916 A;

U&С2 = −Z 2 I&C 2 = −(2.5 + j7.5)(2.443 − j4.916) = −42.968							− j6.032 B;
U&ДвC 2 =U&С2 = −42.968 − j6.032 B;
I&ДвC 2 =	U&	ДвC 2	=	−42.968 − j6.032	= −1.84	+ j0.618 B;
	Z Дв2			20 + j10

I&ГC 2 = I&C 2 + I&ДвC 2 = 0.603 − j4.298 A; U&ГC 2 = Z Г2 I&ГC 2 = 42.98 + j6.03 B ,

причём U&ГC 2 = −U&C 2 – верно.

Затем находим симметричные составляющие нулевой последовательности напряжений и токов фазы С:

I&С0 = I&3С = 2.443 − j4.916 A;

U&С0 = −Z 0 I&C0 = − j5(2.443 − j4.916) = −24.58 − j12.25 B;

U&n = 0; U&N =U&С0 = −24.58 − j12.25 B;

I&ДвC0 = 0; U&ДвC0 = 0;

I&ГC0 = I&C0 = 2.443 − j4.916 A;

U&ГC0 = Z Г0 I&ГC0 = 24.58 + j12.215 B.

2. Определяем напряжения и токи трёхфазной цепи, используя найденные симметричные составляющие фазы С и фазовый оператор

a = e j120o :

I&ГA = a2 I&ГC1 + aI&ГC 2 + I&ГC0 = −1.755 − j3.144 = 3.6e− j119o A; I&ГB = aI&ГC1 +a2 I&ГC 2 + I&ГC0 =1.45 + j3.759 = 4.03e j69o A;

I&ГC = I&ГC1 + I&ГC 2 + I&ГC0 = 7.634 − j15.363 =17.15e− j64o

= a

= −1.755 − j3.144 = 3.6e

− j119o

I ДвA

ДвC1 + aI ДвC 2

+ I ДвC0

=1.45 + j3.759 = 4.03e

j69o

I ДвB

= aI

ДвC1 + a

I ДвC 2

+ I ДвC0

I&ДвC = I&ДвC1 + I&ДвC 2 + I&ДвC0 = 0.305 + j0.615 = 0.686e− j64o A;

=15.848 − j105.956 =107.135e

− j81.5o

U ГA

= a U

ГC1 +aU ГC 2

+U ГC0

= −132.64 + j32.6 =136.588e

− j166o

U ГB

= aU ГC1 +a UГC 2 +U ГC0

U&ГC =U&ГC1 +U&ГC 2 +U&ГC0 =190.54 + j110.005 = 220e j30o B;

102.2e

− j85o

U ДвA = a U ДвC1 + aU ДвC 2 +U ДвC0 = 8.724 − j101.828 =

2 &

95.617e

j110o

U ДвB = aU

ДвC1 + a U ДвC 2 +U ДвC0 = −33.308 + j89.628 =

U&ДвC =U&ДвC1 +U&ДвC 2 +U&ДвC0 = 24.585 + j12.2 = 27.446e j26o B;

I&N = I&n = 3I&ДвC0 = I&ДвA + I&ДвB + I&ДвC = 0 – верно, т.к. ZN = ∞.

U&n = 0; U&N

=U&C0

= −24.58 − j12.215 = 27.448e− j153.6o B.

При замыкании фазы С на N и при ZN = ∞ имеем:

ГC

= E&

; I&

= I&

ДвA

; I&

= I&

ДвB

; U&

= −U&

ДвC

– верно.

ГA

ГB

3.Рассчитываем балансы активной и реактивной мощностей.

3.1.Комплекс полной вырабатываемой мощности:

S&B = E&A I&ГA + E&B I&ГB + E&C I&ГC =

=220e− j90o (3.6e j119o ) +220e− j 210o (4.03e− j69o ) +220e j30o (17.15e j64o ) =

=568.2 + j5023 BA;

где PB = 568.2 Вт > 0 – активная вырабатываемая мощность; QB = 5023 вар – реактивная вырабатываемая мощность.

3.2. Потери полной мощности в обмотках генератора:

S&Г =U&ГA I&ГA +U ГB I&ГB +U ГC I&ГC =

=107.135e− j81.5o (3.6e j119o ) +136.588e− j166o (4.03e− j69o ) + +220e j30o (17.15e j64o ) = −24.289 + j4545 BA;

QГ = 4545 вар; PГ = −24, 289 Вт ≈ 0 , т.к. RГ = 0 и QГ PГ .

3.3. Потребляемая двигателем полная мощность:

S&Дв =U&ДвA I&ДвA +U&ДвB I&ДвB +U&ДвC I&ДвC =

=102.2e− j85o (3.6e j119o ) +95.617e j110o (4.03e− j69o ) +

+27.446e j26o (0.686e j64o ) = 595.837 + j477.37 BA; где PДв = 595.837 Вт ; QДв = 477.37 вар.

3.4. Потребляемая в нулевом проводе полная мощность.

S&0 =U&n I&n +U&N I&N = 0 0 +27.448e− j153.6o 0 = 0 BA;

где P0 = 0 Вт ; Q0 = 0 вар.

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
25.03.2016282.12 Кб107Rentgen laba.docx
#
29.05.201552.54 Кб10resursy_Roo.docx
#
29.05.201533.66 Кб17Reyting.docx
#
29.05.2015168.45 Кб491rezba.doc
#
29.05.2015873.07 Кб15RGR-3_813.rtf
#
29.05.2015726.41 Кб19RGR_1.pdf
#
03.05.2019110.59 Кб5risk-management.doc
#
18.11.2018294.4 Кб61Rok-muzyka_v_interesah_uchaschihsya_10-11_klass....doc
#
29.05.20152.22 Mб27rp.pdf
#
29.05.2015743.73 Кб21rp.pdf
#
29.05.2015321.02 Кб16rpstand 8Г10.doc