
МАРЭС
.pdf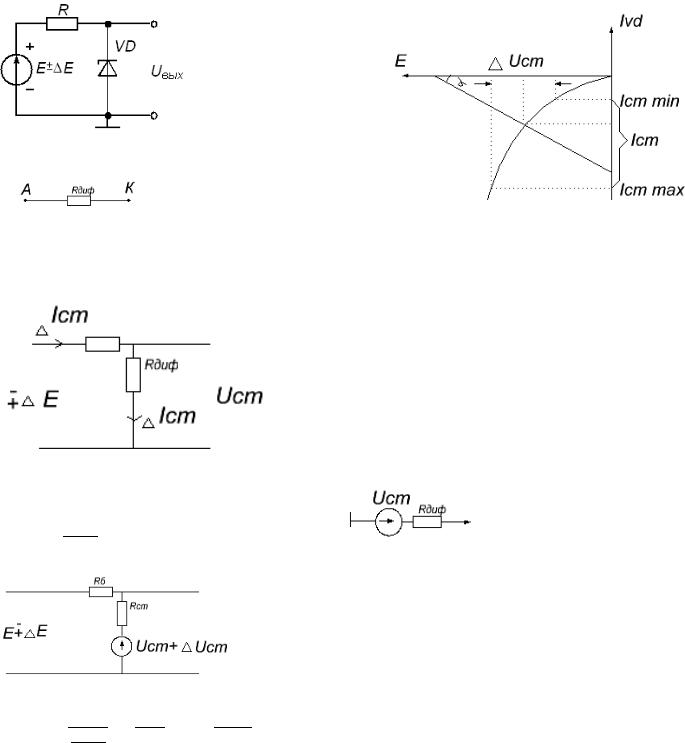
1. Проанализировать работу источника опорного напряжения, используя схемную модель линейных приращений и локальную модель р-n перехода
R – тоже самое что Rб
Е = т ∙ б + ст;
Строим нагрузочную прямую:
б = ; |
|
|
|
|
|
|
|
|||||
диф = |
∆ст |
|
|
|
|
|
|
|
|
|
|
|
ст |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
Вместо стабилитрона ставим схемную замену: |
|
|
|
|
|
|
|
|||||
|
|
= |
вых |
= |
∆ст |
= |
диф |
= |
|
1 |
, Если Rдиф |
|
|
|
|
|
|
|
б |
||||||
|
|
|
вх |
∆Е |
диф+ б |
1+ диф |
||||||
|
|
|
|
|
|
|||||||
стремится к 0, то К тоже к 0;
Рассмотрим локальную модель:
0, если д < ст
ст = ∆ст
диф
, если д ≥ ст ;
∆Е
ст = ∆Е т = Ест (1 + дифб ).
ст

2. Записать и пояснить алгоритм получения параметров схемной модели линейных приращений компонентов электронных схем на примере биполярного транзистора.
Алгоритм:
рисуем типовую схему включения прибора (смотри выше)
записываем уравнение электрического равновесия
записываем (строим) уравнение ВАХ в интересующем диапазоне к = ( б, кэ)
решаем совместно уравнения п2 и п3 что задает положение рабочей точки А
задаем в окрестностях раб точки А приращения ∆, ∆
определяем диф параметры прибора в окрестности раб точки
А
1)Ек = кэ + к ∙
2)к = ( б, кэ)
Нужно совместно решить эти два уравнения. Так как второе мы не можем записать в аналитическом виде, то строим ВАХ.
3) характеристики (рисунки)
Ек
4) строим нагрузочную прямуюпрямую по 2 крайним точкам. 2 точки: иЕк. Так же
бА = кА
5) 11 = ∆∆ бб, 22 = ∆∆ кк.
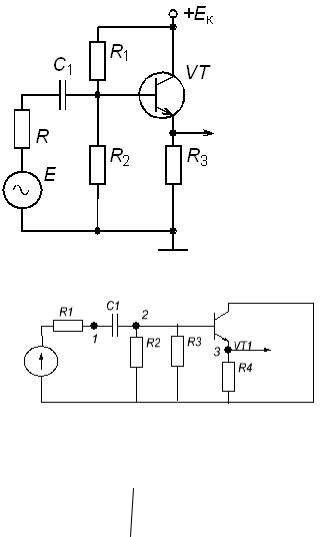
3. Записать обобщенным методом узловых потенциалов математическую модель схемы при заданных Y - параметрах транзистора.
Составим эквивалентную схему замещения по току:
1 + |
|
− |
0 |
|
||
Усх = − |
2 + 3 + |
0 |
, примечание: узлы 1 2 3 |
|||
0 |
|
0 |
4 |
|
||
|
у11 |
у12 |
|
у13 |
|
|
Утранз = |
|
|
|
у23 ; примечание: матрица строится (Б К Э) |
||
у21 |
у22 |
|
||||
|
у31 |
у32 |
|
у33 |
|
|
1 + |
− |
0 |
1 |
|
1 |
У = − |
2 + 3 + + 11 |
13 |
; = 0 |
; = |
2 |
0 |
31 |
4 + 33 |
0 |
|
3 |
1 + |
− |
0 |
1 |
1 |
− |
2 + 3 + + 11 |
13 |
0 |
= 2 |
0 |
31 |
4 + 33 |
0 |
3 |
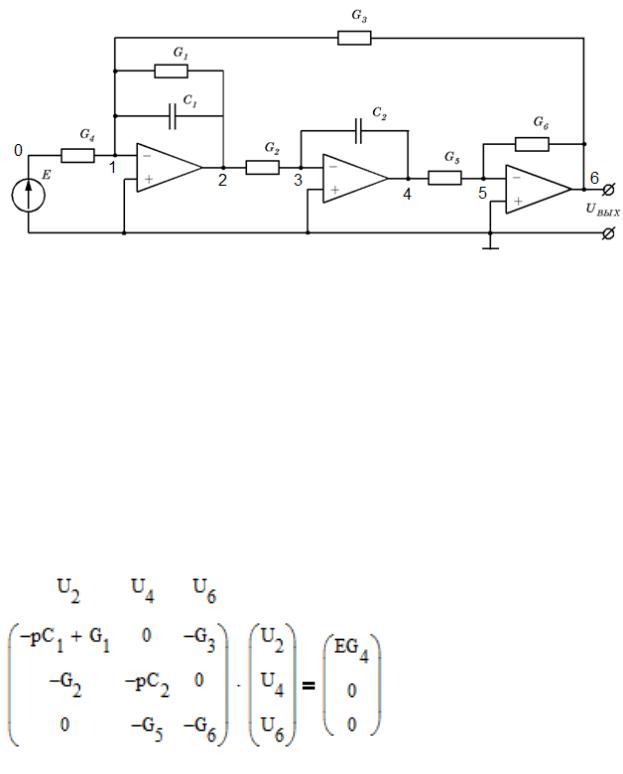
4.Записать частным методом узловых потенциалов математическую модель схемы на ОУ
Решение: Большинство интегральных схем на эквивалентных схемах можно представить в виде источника напряжения. Для источников ЭДС узловые уравнения не записываются, т.к. потенциал узлазадан оприори=> уравнения Кирхгофа для них не нужно. Для идеальных ОУ (Rвх=∞, Rвых=0, А=∞) разность потенциалов на диф. входе принимаем=0
(U1-U2=0).
Uвыхоу ≤ Uпит; А → ∞
Uвых = U1 − U2 ∙ A ; Uвых → конечноечисло; U1 − U2 → 0; A → ∞ .
Если один из входов ОУ заземлен -0, то и потенциал другого входа принимаем =0, тогда
для узлов 0,2,4,6 уравнения не составляем, потенциалы узлов 1,3,5 равны 0.
Узел 1: 4 + 1 + 1 + 3 1 − 1 + 1 2 − 3 6 = 4 Узел 3: − 2 2 + 2 + 2 3 − 2 4 = 0 Узел 5: − 5 4 + 5 + 6 5 − 6 6 = 0
Т.o. математическая модель схемы будет иметь вид:
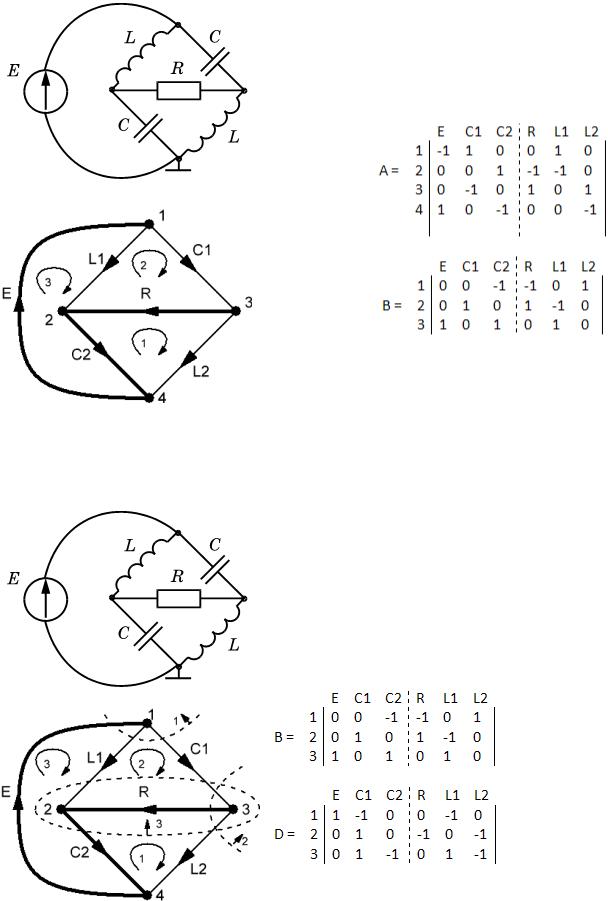
5. Выбрать дерево графа и показать, что = .
Выбираем дерево, нумеруем узлы и расставляем направления токов. Составим матрицы инциденций А и В. Матрица А: если ток втекает, то «-1», если вытекает, то «1», если не касается, то «0». Матрица В: если направление контура (выбираем сами) совпадает с направлением ветви, то «1», если не совпадает, то «- 1», если не касается, то «0».
Перемножим матрицы А и ВТ по правилу умножения матриц:
|
|
0 |
0 |
0 |
T |
|
0 |
0 |
0 |
A B |
0 |
0 |
0 |
|
|
|
|||
|
|
|
|
|
|
|
0 |
0 |
0 |
6. Выбрать дерево графа и показать, что = .
Выбираем дерево, нумеруем узлы и расставляем направления токов. Составим матрицы инциденций В и D. Матрица В: если направление контура (выбираем сами) совпадает с направлением ветви, то «1», если не совпадает, то «-1», если не касается, то «0». Матрица D: если направление сечения (выбираем сами) совпадает с направлением тока в ветви, то «1», если не совпадает, то «-1», если не касается, то «0».
Перемножим матрицы B и DТ по правилу умножения матриц:
0 0 0 B DT 0 0 0
0 0 0
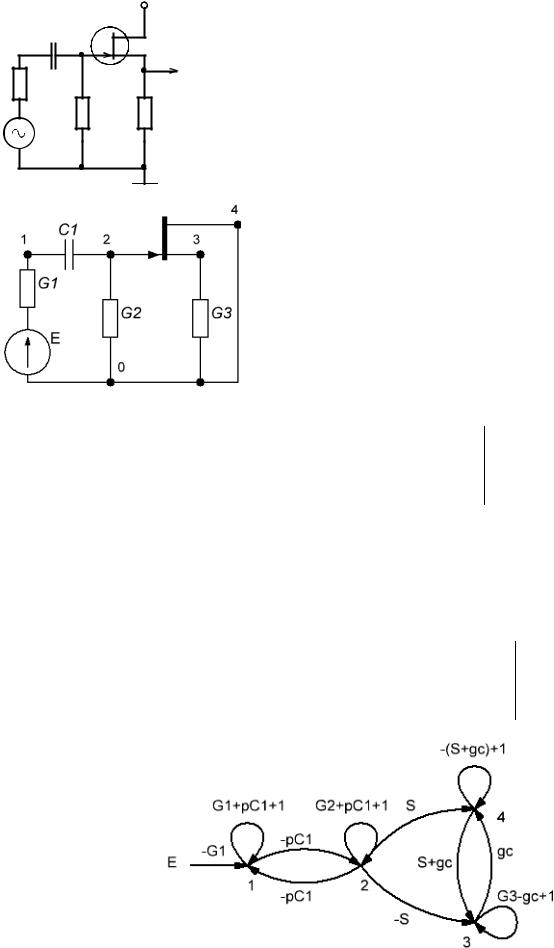
7. Косвенным методом построить СГ цепи на дискретных компонентах.
|
+Ec |
VT |
|
C1 |
|
G |
|
G1 |
G2 |
E |
|
Составим эквивалентную схему замещения и пронумеруем узлы:
Мысленно изымаем многополюсник и составляем матрицу проводимости оставшейся схемы:
|
1 |
2 |
3 |
4 |
1 |
G1+pC1 |
-pC1 |
0 |
0 |
Y’ = 2 |
-pC1 |
G2+pC1 |
0 |
0 |
3 |
0 |
0 |
G3 |
0 |
4 |
0 |
0 |
0 |
0 |
Составим матрицу проводимости многополюсника (не меняя нумерацию узлов):
|
|
з (2) |
и (3) |
с (4) |
||
|
з (2) |
0 |
0 |
|
0 |
|
Y’’ = и (3) |
-S |
-gC |
|
S + gC |
|
|
|
с (4) |
S |
gC |
|
-(S + gC) |
|
Суммируем матрицы Y’ и Y’’: |
|
|
|
|
|
|
|
1 |
2 |
|
3 |
4 |
|
1 |
G1+pC1 |
-pC1 |
|
0 |
0 |
|
Y = 2 |
-pC1 |
G2+pC1 |
0 |
0 |
|
|
3 |
0 |
-S |
|
G3 - gC S + gC |
||
4 |
0 |
S |
|
gC |
-(S + gC) |
|
Строим сигнальный граф: |
|
|
|
|
|
|
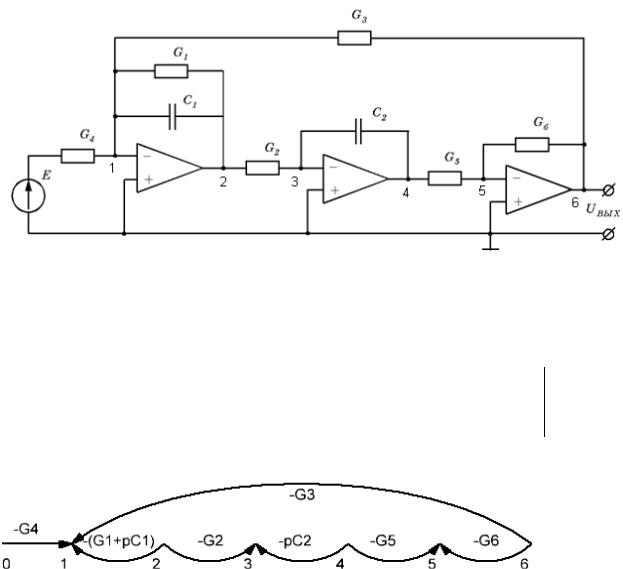
8. Косвенным методом построить СГ цепи на ОУ.
Нумеруем узлы. ОУ можно представить в виде источника напряжения, управляемого напряжением. А для источников напряжения узловые уравнения не записываются. Значит, для узлов 0,2,4,6 уравнения не составляем, а потенциалы узлов 1,3,5 равны нулю ( U=0). Схемное уравнение электронной цепи будет иметь вид:
|
2 |
4 |
6 |
|
|
|
|
1 |
-(G1+pC1) |
0 |
-G3 |
|
U2 |
|
E G4 |
Y = 3 |
-G2 |
-pC2 |
0 |
x |
U4 |
= |
0 |
5 |
0 |
-G5 |
-G6 |
|
U6 |
|
0 |
По системе уравнений строим нормализованный сигнальный граф:
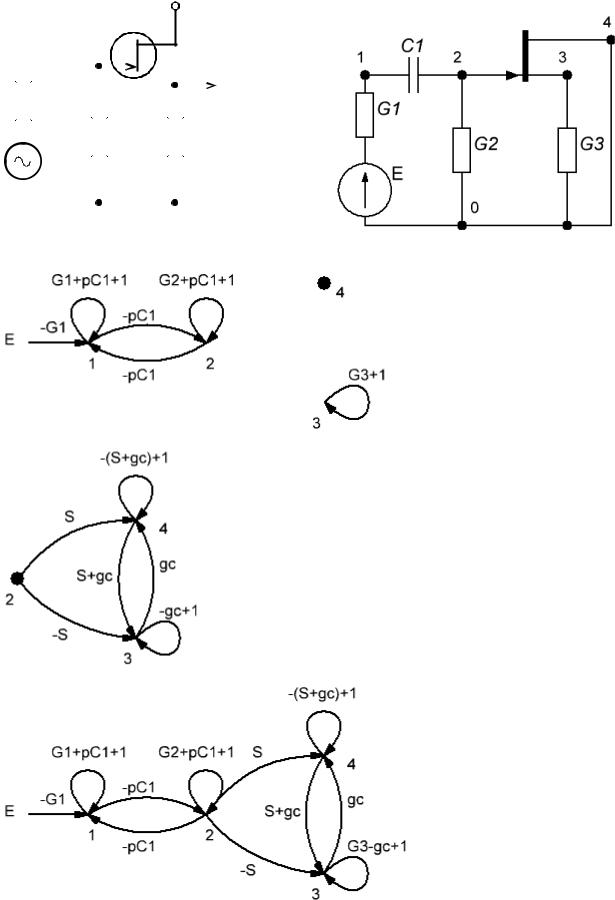
9. Прямым методом построить СГ цепи на дискретных компонентах.
+Ec
Составим эквивалентную схему замещения и пронумеруем узлы:
VT
C1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
||||
|
|
E |
|
|
G1 |
|
|
G2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Мысленно изымаем многополюсник и строим СГ оставшейся части схемы:
Строим СГ многополюсника:
Объединяем два СГ, получаем:
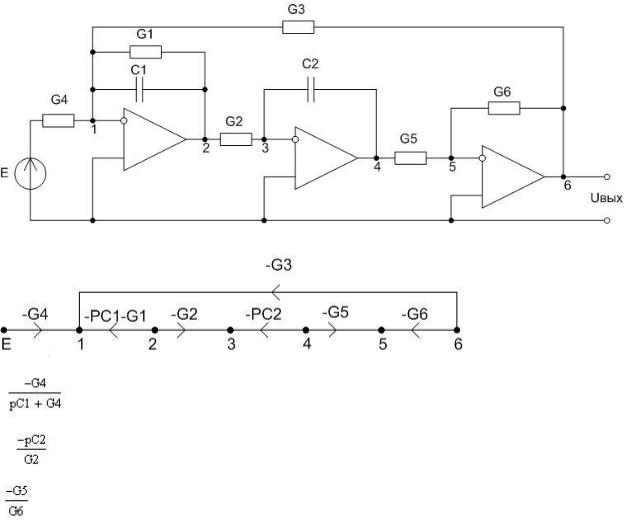
10. Прямым методом построить СГ цепи на ОУ.
Непосредственно по схеме строим сигнальный граф (СГ)
-Коэффициент усиления первого ОУ
-Коэффициент усиления второго ОУ
-Коэффициент усиления третьего ОУ
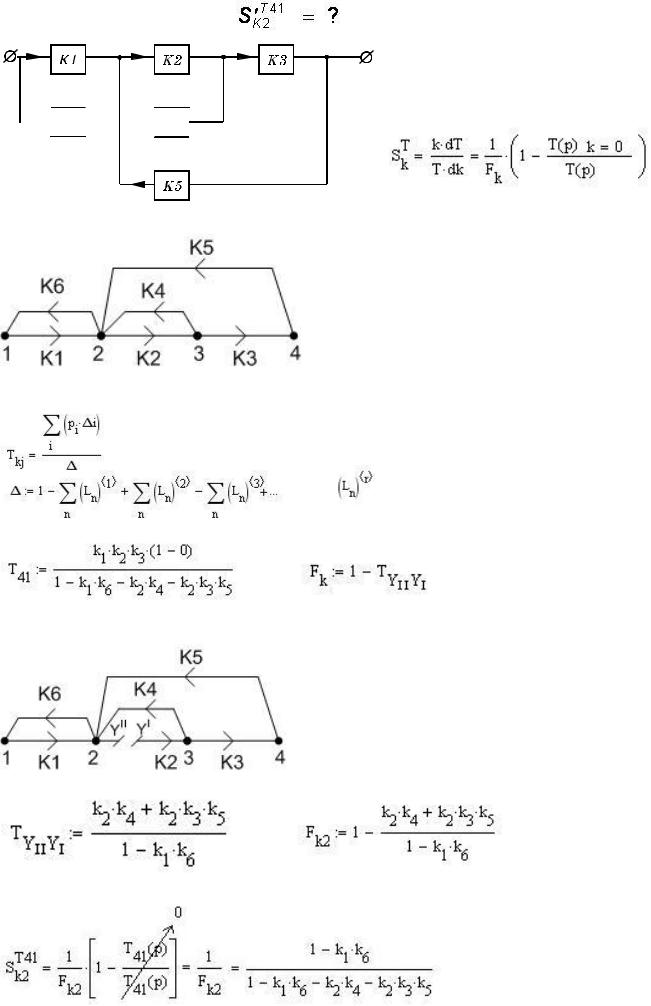
11. Найти чувствительность схемной функции относительно заданного параметра методом СГ.
 K6
K6 

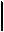
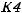
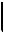
Строим сигнальный граф (СГ) схемной функции:
 - чувствительность коэффициента передачи относительно К, характеризует степень изменения коэффициента передачи при изменении величины К и определяется:
- чувствительность коэффициента передачи относительно К, характеризует степень изменения коэффициента передачи при изменении величины К и определяется:
по формуле Мезона найдём коэффициент передачи 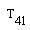 (передача графа от узла 1 к 4 узлу)
(передача графа от узла 1 к 4 узлу)
где 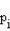 - i-тый путь от узла j к узлу k;
- i-тый путь от узла j к узлу k;
 - определитель части графа не касающегося i-того пути;
- определитель части графа не касающегося i-того пути;
где - алгебраическая сумма коэффициентов передачи n комбинаций из r не касающихся контуров;
возвратная разность.
Разорвём ветвь К2:
