Прямая линия на плоскости. Взаимное расположение прямых

Всякое уравнение первой степени относительно и, т. е. уравнение вида

, (6)

где ,и- постоянные коэффициенты, причем, определяет на плоскости некоторую прямую. Это уравнение называетсяобщим уравнением прямой.

Если в общем уравнении прямой , то разрешив его относительно, получим уравнение прямой с угловым коэффициентом

, (7)

где - тангенс угла, образованного прямой с положительным направлением оси;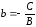- ордината точки пересечения прямой с осью.

Уравнение (8)

является уравнением прямой, которая проходит через точку и имеет угловой коэффициент.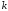

Если в общем уравнении прямой , то, разделив все члены на, получим уравнение прямой «в отрезках»

, (9)

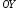где ,– величины направленных отрезков, отсекаемых прямой на осях координати, соответственно.

Уравнение

, (10)

является уравнением прямой, проходящей через две точки и.

Обозначим ,координаты направляющего вектора прямой, тогда (10) примет вид

, (11)

где – точка на прямой. Уравнение (11) называетсяканоническим уравнением прямой. Введя параметр , из (10) получимпараметрические уравнения прямой

где (12)

Уравнение прямой, проходящей через точку перпендикулярно вектору, имеет вид

. (13)

Вектор – называетсянормальным вектором прямой. Раскрывая в (13) скобки, получим общее уравнение прямой

.

Таким образом, в общем уравнении прямой, коэффициенты при исуть координаты нормального вектора прямой.

Пусть две прямые заданы уравнениями с угловыми коэффициентами и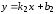. Возможны следующие случаи их взаимного расположения:

1. прямые параллельны (в частности совпадают) тогда и только тогда, когда выполняется условие ;

2. прямые пересекаются в некоторой точке, тогда угол между ними находится по формуле ;

3. прямые перпендикулярны тогда и только тогда, когда .

Пример. В равнобедренном прямоугольном треугольнике даны декартовы координаты вершины острого угла и уравнение противолежащего катета. Составить уравнения двух других сторон этого треугольника.

Решение.

Найдем уравнение прилежащего катета. Так как ,, то уравнениеимеет вид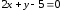.Угол между катетом и гипотенузой в равнобедренном треугольникеравен. Для нахождения уравнения гипотенузы воспользуемся формулой, из которой найдем угловой коэффициент прямой.

1. .

Тогда уравнение имеет вид

2. .

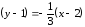
Тогда уравнение

Ответ: ,

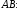
Прямая и плоскость в пространстве

Плоскость в декартовой системе координат может быть задана следующими уравнениями:

1. Общее уравнение плоскости

.

Кроме того,

уравнение плоскости, которая проходит через точку перпендикулярно вектору.

2. Уравнение плоскости “в отрезках”

,

где – величины направленных отрезков, отсекаемых плоскостью на координатных осях,и, соответственно.

3. Уравнение плоскости, проходящей через три точки ,,

.

Прямая в пространстве задается:

1. общими уравнениями в пространстве в

где , таким образом, прямая задана как линия пересечения двух плоскостей.

2. каноническими уравнениями в

,

где – точка, принадлежащая прямой, а– направляющий вектор.

3. параметрическими уравнениями

Пример. Составить уравнение плоскости, проходящей через точку и прямую.

Решение.

Уравнение плоскости, проходящей через точку и имеющей координаты вектора нормали, имеет вид

.

Найдем координаты вектора нормали. – данная точка,– точка, лежащая на нашей прямой,– координаты направляющего вектора прямой. Тогда

.

Запишем уравнение искомой плоскости

,

,