ответы на первую часть (терм)

8,9,10,11,1214,1521,23

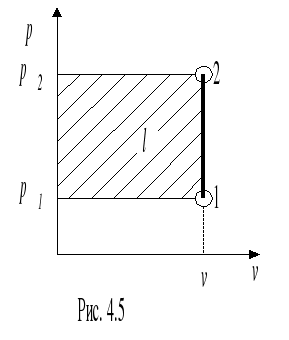
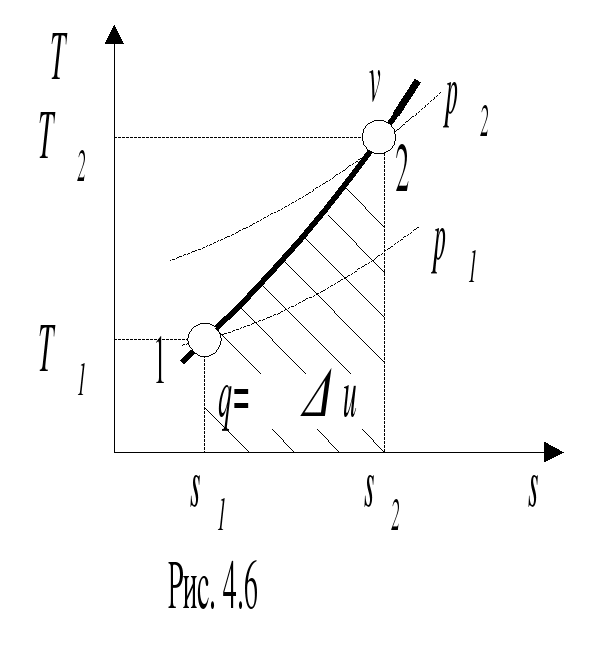
4. Расчёт изохорного процесса идеального газа. Изобразить процесс в p-v и T-S диаграммах.

,,

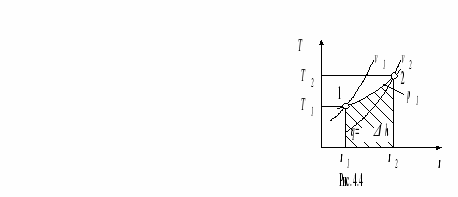
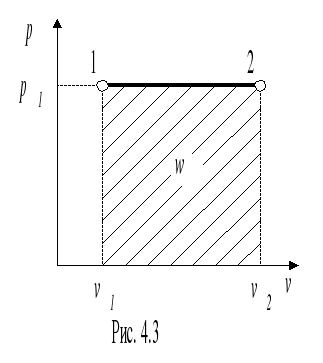
4. Расчет изобарного процесса

6. Изотермический процесс идеального газа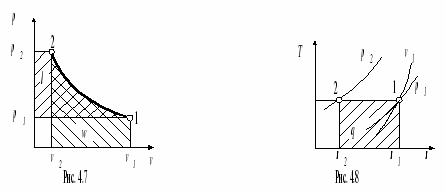

7. Дифференциальная связь для s=f(T,p) Использование этой связи для расчёта энтропии.

8. Расчитать политропный процесс идеального газа (О₂) при заданных р1, v1, р2(р2˃р1) n=1,6 (n=0,85).Изобразить процесс вp-v, T-S – диаграммах

9. Расчитать политропный процесс идеального газа (О₂) при заданных р1, v1, р2(р2˂р1) n=1,6 (n=0,85). Изобразить процесс вp-v, T-S – диаграммах

10. Рассчитать адиабатный процесс идеального газа при заданных p1,t1, р2˃р1 . Изобразить процесс вp-v, T-S – диаграммах

13. Расчёт калорических параметров идеальных газов и их смесей

Внутренняя энергия (u), энтальпия (h), энтропия (s) являются калорическими параметрами и рассчитываются по формулам через термические параметры p, v, T. Расчетные формулы могут быть получены на основании дифференциальных связей термодинамики

,

Калорические параметры смесей идеальных газов рассчитываются по формулам вида

, Дж/кг, , Дж/кг, Дж/(кг.К).

16. Анергия и эксергия. Эксергетический КПД. Понятие. Расчёт.

Работоспособность, термин, применяемый в термодинамике для обозначения максимальной работы, которую может совершить система при переходе из данного состояния в равновесие с окружающей средой. Вторую составляющую А, наз. анергией (от греч. "а" - отрицат. частица и ergon - работа), ни в какую иную форму энергии, включая мех. работу, превратить нельзя.

Эксергетический кпд системы. Диаграммы Грассмана и непосредственно эксергетич. баланс в форме ур-ния позволяют найти количеств, показатели эффективности работы анализируемой ХТС. Среди этих показателей наиб. распространен эксергетич. кпд определяемый соотношением:

где - сумма потоков эксергий, отражающая полезный эффект от функционирования системы;- полные затраты эксергий на достижение заданного эффекта.  Для идеального, полностью обратимого процесса, в к-ром потери отсутствуют,= 1; если подведенная эксергия полностью теряется в процессе, то= 0. В реальных процессах всегда соблюдается неравенство: 0 << 1; при этом чем выше численное значение тем термодинамически совершеннее система. Из ф-лы (13) следует также, что разность между эксергиями, обусловливающими полезный эффект и эксергетич. затраты, всегда равна суммарной потере эксергий от необратимости протекающих в системе процессов

17. Параметры торможения в адиабатном потоке пара Н₂О.

Параметры торможения потока водяного пара с характеристиками p₁, t₁, скоростью c₁ определяются с помощью диаграммы либо по таблицам воды и водяного пара. При этом энтальпию (h₀) рассчитывают по уравнению:

Принимая процесс торможения (1-0) адиабатным, параметры p₀, T₀, v₀ находят в точке пересечения s₁ и h₀ (точка 0, рис. 6.4).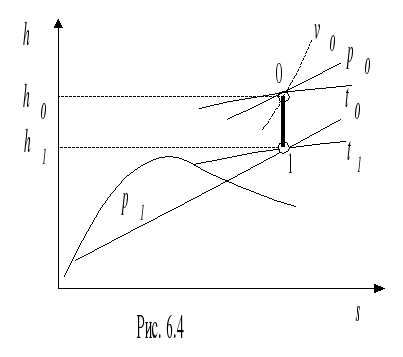

(6.7)

Подставляя в (6.7), получаем

.

(6.8)

Давление и объем в состоянии торможения рассчитываются по уравнениям

,

22. Температура торможения в адиабатном потоке идеального газа.

температура Т0 изоэнтропически (без теплообмена с внешней средой) заторможенного газа. Играет важную роль при движении идеального совершенного газа; в так называемом адиабатическом течении она соответствует максимально возможной температуре газа и характеризует его полную удельную энергию, которая остаётся постоянной вдоль линии тока. При отсутствии массовых сил её значение вычисляется на основе Бернулли уравнения:  T0=T + V2/2cp,  где Т — температура, V — скорость, cp — удельная теплоёмкость газа при постоянном давлении. Часто используется в аэродинамических расчётах в качестве характерного масштаба температуры.

25. Термические параметры состояния рабочего тела(давление объём, температура. Уравнение состояния идеального газа.

К основным параметрам состояния, поддающимся непосредственному измерению простыми техническими средствами, относятся абсолютное давление , удельный объём  и абсолютная температура . Эти три параметра носят название термических параметров состояния.

Объём — количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами.

Давле́ние  — физическая величина, численно равная силе F, действующей на единицу площади поверхности S перпендикулярно этой поверхности. В данной точке давление определяется как отношение нормальной составляющей силы , действующей на малый элемент поверхности, к его площади:

Температу́ра (от лат. temperatura — надлежащее смешение, нормальное состояние) — скалярная физическая величина, характеризующая состояние термодинамического равновесиямакроскопической системы. Температура всех частей системы, находящейся в равновесии, одинакова. Если система не находится в равновесии, то между её частями, имеющими различную температуру, происходит теплопередача (переход энергии от более нагретых частей системы к менее нагретым), приводящая к выравниванию температур в системе.

Уравнение состояния идеального газа— формула, устанавливающая зависимость между давлением,молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид: , где — давление, — молярный объём, — универсальная газовая постоянная,  — абсолютная температура,К.

18. Критические параметры при истечении, критическая скорость, отношение давлений и температур для идеального газа.

19. Теплоемкость: истинная и средняя. Связь между ними. Ср и сv. Уравнение Майера. Теплоемкость смеси. !!!!!!!!!!!!!!!!!!!!!!!!

Теплоемкостью тела называют кол-во теплоты, необходимой для нагрева тела на один градус.

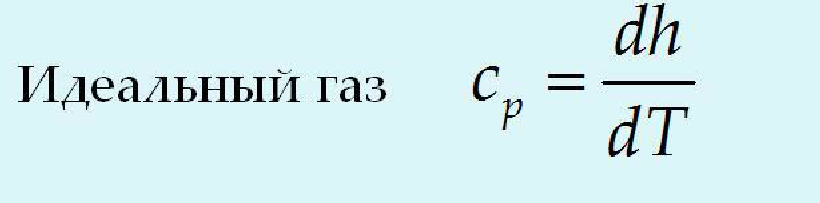24. Дифференциальные связи термодинамики. Их назначение, получение(на примере одной по выбору) и использование для расчёта параметров идеального газа. !!!!!!!!!!!!!!!

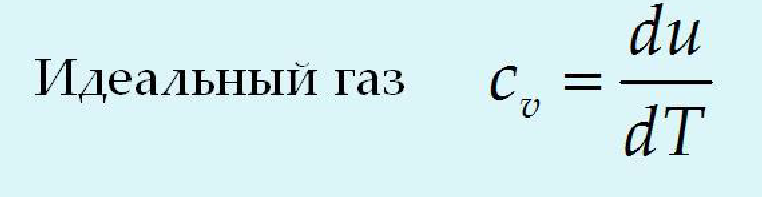
Вторые вопросы:

9 вопрос.Первый зк термод. Продолжение на фото Аня!

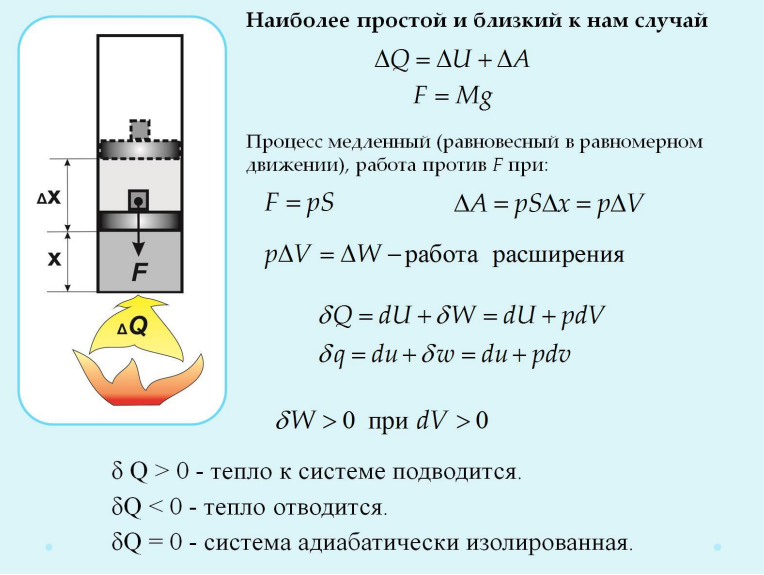
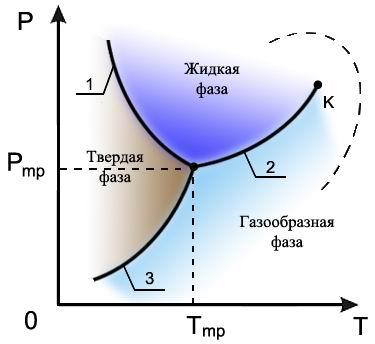
 При описании состояния вещества и его фазовых переходов обычно используются переменные  и , в которых изображаются кривые равновесия при фазовых переходах данного вещества. Диаграмма, построенная в этих переменных, называется диаграммой состояния. Каждой точке на этой диаграмме соответствует определенное равновесное состояние. Она позволяет определить, какие фазовые переходы происходят при тех или иных процессах.

     Рассмотрим случай термодинамической системы, в которой в равновесии находятся сразу три фазы однородного по физико-химическим свойствам вещества (например: лед, вода и пар). Равновесие такой системы будет наблюдаться при одновременном выполнении трех условий, соответствующих равновесию этих фаз между собой. Эти условия в общем виде можно записать в форме

     

.

(7.52)

     Равенства (7.52) приводят к системе из двух независимых уравнений

     

,

(7.53)

     

.

(7.54)

     Решение этой системы уравнений при условии отсутствия химических превращений дает совершенно определенные значения давления  и температуры , при которых три фазы могут существовать одновременно. Точка на диаграмме состояния в переменных  и  (см. рис. 7.6), соответствующая указанным значениям давления и температуры, называется тройной точкой. В этой точке встречаются кривая плавления 1, разделяющая твердую и жидкую фазы, кривая испарения 2, разделяющая жидкую и газообразную фазы, и кривая возгонки 3, разделяющая твердую и газообразную фазы.

Рис. 7.6. Диаграмма состояния  1 - кривая плавления, 2 - кривая испарения, 3 - кривая возгонки

     Кривая испарения 2 заканчивается критической точкой (К), в которой исчезают отличия жидкой и газообразной фаз. Если фазовый переход осуществляется в обход критической точки, как показано пунктирной линией на рис. 7.6, то пересечения кривой испарения не происходит и фазовое превращение проходит путем непрерывных изменений без образования границы раздела фаз.

     Для однородного по своим физико-химическим свойствам вещества в равновесии одновременно могут находиться не более трех фаз. Это означает, что для равновесной системы могут существовать только точки, в которых сходятся три фазы вещества, например, соответствующие трем его агрегатным состояниям. Точки, в которых могли бы одновременно существовать более трех фаз, не реализуемы.

     Вещество в трех различных агрегатных состояниях может наблюдаться и при значениях температуры и давления, не соответствующих тройной точке. Например, в природе при различных погодных условиях наблюдаются одновременно лед, вода и водяной пар (последний, как правило, косвенным образом). Однако, в отличие от состояния в тройной точке, указанные состояния не являются равновесными, и для них характерен постоянный переход вещества из одной фазы в другую.

     Значения давления и температуры в тройной точке для различных веществ очень стабильны, что позволяет использовать тройную точку для калибровки различных температурных шкал. Тройная точка воды используется в качестве основной реперной точки для температурных шкал Кельвина и Цельсия (см. параграф 1.3).

     Отличительной особенностью гелия, диаграмма состояния которого схематически изображена на рис. 7.7, является отсутствие тройной точки, соответствующей одновременному равновесному существованию твердой, жидкой и газообразной фаз.