Дифракция от круглого |
|
|
отверстия |
r |
r |
S |
|
|
r0 |
O |
|
|
Р |
I |
I |
|
|
a |
|
b |
|
|
|
||
|
ab |
|
|
|
|
|
|
m - нечетное |
m - четное |
r |
|
m |
|
|
|
|
|
|
|
0 |
a b |
|
A |
A |
|
A |
|
|
|
|
|
|
|
1 |
m |
|
|
||
|
|
|
|
|
2 |
|
2 |
|
|
m |
r2 |
1 |
|
1 |
|
|
|
0 |
|
|
|
зависит от число открытых зон Френеля, |
|||
|
b |
||||||
|
a |
|
|
«+» - для нечетных «-» – для четных |
Дифракция от круглого
отверстия
Дифракционная картина от круглого отверстия – чередование светлых и темных концентрических полос.
m – нечетное, в центре светлое пятно
A A21 A2m
m – четное, в центре темное пятно
A A21 A2m
Дифракция от круглого
Дифракция Фраунгофера
от щели
Плоская монохроматическая волна
b
|
- разность хода |
Собирающая линза
Экран, в фокальной плоскости линзы
Р
Дифракция Фраунгофера 
от щели
Амплитуда световых волн в точке Р на экране, которая находится под углом φ к оптической оси линзы задается формулой
|
|
A |
|
A sin[( / )bsin ] |
|
||
|
|
|
|
||||
|
|
|
|
0 |
( / )bsin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
амплитуда при угле φ=0 |
|
||||
При значениях φ, удовлетворяющих условию |
|
||||||
( / )bsin m |
|
|
|
A |
0 |
||
|
bsin m |
|
|
|
|
||
|
m 1,2,... |
|
|||||
Условие положение минимумов интенсивности
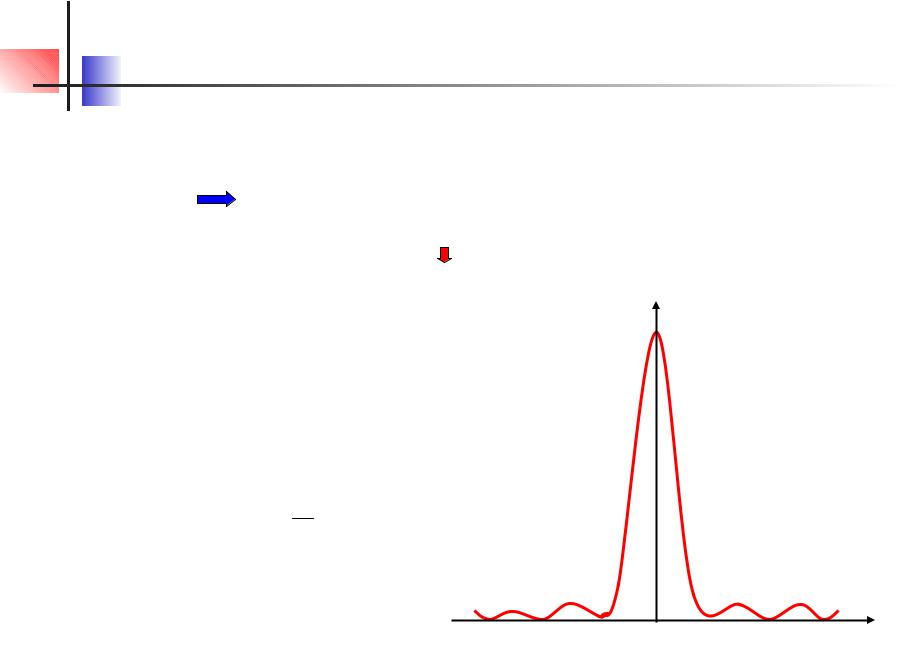
Дифракция Фраунгофера 
от щели
I ~ A2 |
I |
|
I |
sin2 |
[( / )bsin ] |
|
0 [( / )bsin ]2 |
||||||
|
|
|
||||
дифракционная картина будет симметрична относительно центра |
|
линзы |
I |
в середине дифракционной картины образуется максимум освещенности
количество минимумов интенсивности определяется:
m b
|
|
|
2 |
|
sin |
2 b |
b |
b |
2 |
|
Дифракционная решетка 
(2/6)
Разность хода лучей от соседних щелей равна
d sin
Учитывая условия интерференционного максимума
m (m 0,1,2,....)
d sin m
условие главного максимума для дифракционной решетки, где m порядок главного максимума
Минимумы интенсивности наблюдаются при
bsin k
Дифракционная решетка
(3/6)
Кроме дифракционных минимумов, возникающих при возникают еще добавочные минимумы (интерференционные минимумы) между соседними главными максимумами, при
bsin k
d sin m
N
где m’ принимает целочисленные значения коме 0, N, 2N …
Между двумя соседними главными максимумами расположены N-1 интерференционных минимумов, расположенных в свою очередь между слабыми вторичными максимумами
Дифракционная решетка 
(4/6)