64. Вывод табличных производных. Производная постоянной.

При выводе самой первой формулы таблицы будем исходить из определения производнойфункции в точке. Возьмем , где x – любое действительное число, то есть, x – любое число из области определения функции . Запишем предел отношения приращения функции к приращению аргумента при :

Следует заметить, что под знаком предела получается выражение , которое не являетсянеопределенностью ноль делить на ноль, так как в числителе находится не бесконечно малая величина, а именно ноль. Другими словами, приращение постоянной функции всегда равно нулю.

Таким образом, производная постоянной функции равна нулю на всей области определения.

Производная степенной функции.

Формула производной степенной функции имеет вид , где показатель степени p – любое действительное число.

Докажем сначала формулу для натурального показателя степени, то есть, для p = 1, 2, 3, …

Будем пользоваться определением производной. Запишем предел отношения приращения степенной функции к приращению аргумента:

Для упрощения выражения в числителе обратимся к формуле бинома Ньютона:

Следовательно,

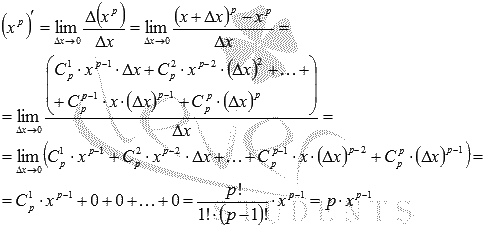
Этим доказана формула производной степенной функции для натурального показателя.

Производная показательной функции.

Вывод формулы производной приведем на основе определения:

Пришли к неопределенности. Для ее раскрытия введем новую переменную , причем при . Тогда . В последнем переходе мы использовали формулу перехода к новому основанию логарифма.

Выполним подстановку в исходный предел:

Если вспомнить второй замечательный предел, то придем к формуле производной показательной функции:

Производная логарифмической функции.

Докажем формулу производной логарифмической функции для всех x из области определения и всех допустимых значениях основания a логарифма. По определению производной имеем:

Как Вы заметили, при доказательстве преобразования проводились с использованием свойств логарифма. Равенство справедливо в силу второго замечательного предела.

Производные тригонометрических функций.

Для вывода формул производных тригонометрических функций нам придется вспомнить некоторые формулы тригонометрии, а также первый замечательный предел.

По определению производной для функции синуса имеем .

Воспользуемся формулой разности синусов:

Осталось обратиться к первому замечательному пределу:

Таким образом, производная функции sin x есть cos x.

Абсолютно аналогично доказывается формула производной косинуса.

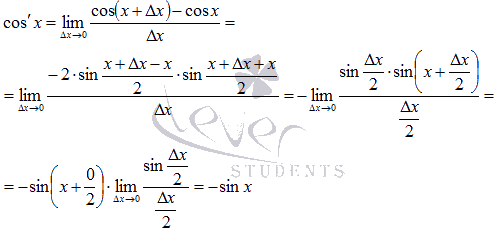
Следовательно, производная функции cos x есть –sin x.

Вывод формул таблицы производных для тангенса и котангенса проведем с использованием доказанных правил дифференцирования (производная дроби).

Производные гиперболических функций.

Правила дифференцирования и формула производной показательной функции из таблицы производных позволяют вывести формулы производных гиперболического синуса, косинуса, тангенса и котангенса.

Производная обратной функции.

Перед началом изучения данной статьи рекомендуем вспомнить определение и свойства обратной функции.

Чтобы при изложении не было путаницы, давайте обозначать в нижнем индексе аргумент функции, по которому выполняется дифференцирование, то есть, - это производная функции f(x) по x.

Теперь сформулируем правило нахождения производной обратной функции.

Пусть функции y = f(x) и x = g(y) взаимно обратные, определенные на интервалах и соответственно. Если в точке существует конечная отличная от нуля производная функции f(x), то в точке существует конечная производная обратной функции g(y), причем . В другой записи .

Можно это правило переформулировать для любого x из промежутка , тогда получим .

Давайте проверим справедливость этих формул.

Найдем обратную функцию для натурального логарифма (здесь y – функция, а x- аргумент). Разрешив это уравнение относительно x, получим (здесь x – функция, а y – ее аргумент). То есть, и взаимно обратные функции.

Из таблицы производных видим, что и .

Убедимся, что формулы нахождения производных обратной функции приводят нас к этим же результатам:

Как видите, получили такие же результаты как и в таблице производных.

Теперь мы обладаем знаниями для доказательства формул производных обратных тригонометрических функций.

Начнем с производной арксинуса.

Для обратной функцией является . Тогда по формуле производной обратной функции получаем

Осталось провести преобразования.

Так как областью значений арксинуса является интервал , то (смотрите раздел основные элементарные функции, их свойства и графики). Поэтому , а не рассматриваем.

Следовательно, . Областью определения производной арксинуса является промежуток (-1; 1).

Для арккосинуса все делается абсолютно аналогично:

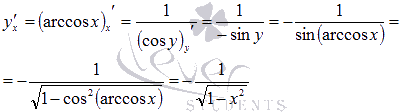
Найдем производную арктангенса.

Для обратной функцией является .

Выразим арктангенс через арккосинус, чтобы упростить полученное выражение.

Пусть arctgx = z, тогда

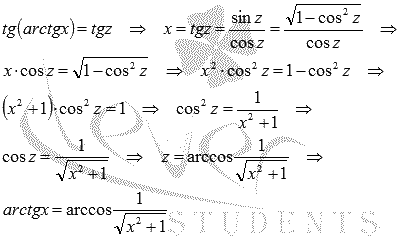
Следовательно,

Схожим образом находится производная арккотангенса: