Физика

9. Равномерное, равнопеременное и переменное движение по окружности. Аналогия между параметрами и уравнениями поступательного движения и движения по окружности.

2. Криволинейное движение

(движение материальной точки по окружности – простейшее криволинейное движение)

а) Равномерное движение материальной точки по окружности (модуль скорости _t не изменяется, но направление скорости изменяется _t 0 изменяется – рис. 18). Полное ускорение равно (12):

; ,т.е. .

Рис. 18

|₁ | = ₂

б) Равнопеременное движение материальной точки по окружности (модуль скорости изменяется, но || = const _t 0 и направление скорости изменяется – § 5). Полное ускорение равно (12):

; .

– Если направления векторов тангенциального ускорения и скорости совпадают (модуль скорости увеличивается: v > v0, но |_n| = const u _n 0 и – рис. 16) – это равноускоренное движение материальной точки по окружности ( () < 90°) – рис. 19.

– Если направления векторов тангенциального ускорения и скорости противоположны: _t (модуль скорости уменьшается: v < v₀, но || = const и _n 0) – это равнозамедленное движение материальной точки по окружности () > 90°) – рис. 19.

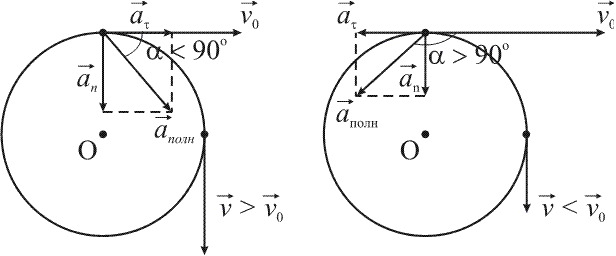
Рис. 19

Задача кинематики: определить положение материальной точки, ее скорость и ускорение в любой момент времени:

Уравнение зависимости радиус-вектора от времени или координат материальной точки от времени движения называют уравнением движения.

Зависимость координат, скорости, проекции скорости, ускорения, проекции ускорения могут быть представлены в виде формул, графиков и таблиц. Решим задачу кинематики для рассмотренных простых видов движения (таблица 1).

Таблица 1

Криволинейное движение  (движение материальной точки по окружности)
Равномерное		Равнопеременное

Законы, определяющие движение тела по окружности, аналогичны законам поступательного движения. Уравнения, описывающие вращательное движение, можно вывести из уравнений поступательного движения, произведя в последних следующие замены:

Если: перемещение s — угловое перемещение (угол поворота) φ, скорость u — угловая скорость ω, ускорение a — угловое ускорение α

Вращательное движение, характеристики

Вращательное движение	Угловая скорость	Угловое ускорение
Равномерное	Постоянная	Равно нулю
Равномерно ускоренное	Изменяется равномерно	Постоянно
Неравномерно ускоренное	Изменяется неравномерно	Переменное

В криволинейном переменном движении вектор нормального ускорения / норм направлен по радиусу круга кривизны к центру, вектор касательного ускорения / нас и вектор скорости V направлены в одну сторону, если движение ускоренное, и в противоположные стороны - если замедленное.

Таким образом, связь между линейными и угловыми величинами выражается следующими формулами: S = R·φ, υ = ω·R, a_τ = R·ε, a_n = ω²·R.

42. Политропический процесс. Уравнение политропы и его частные случаи.

Политропный процесс, политропический процесс — термодинамический процесс, во время которого удельная теплоёмкость газа остаётся неизменной.

В соответствии с сущностью понятия теплоёмкости , предельными частными явлениями политропного процесса являются изотермический процесс () и адиабатный процесс ().

В случае идеального газа, изобарный процесс и изохорный процесс также являются политропными (удельные теплоёмкости идеального газа при постоянном объёме и постоянном давлении соответственно равны и ( и не меняются при изменении термодинамических параметров).