
1-15
.docМинистерство образования Российской Федерации
ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Наименование факультета -ЕНМФ
Наименование выпускающей кафедры –Общей физики
Наименование учебной дисциплины - Физика
Лабораторная работа № 1-15
Наименование работы – Определение модуля Юнга стальной проволоки из растяжения
Исполнитель:
Студент, группы 13А61 ( ) Грубова Р. К.
подпись
(_______)
дата
Руководитель, профессор (_______) Крючков Ю.Ю.
Должность, ученая степень, звание подпись
(_______)
дата
Томск –2007
Определение модуля Юнга стальной проволоки из растяжения.
Цель работы: ознакомление с одним из методов регистрации величины растяжения стальной проволоки при изучении упругой деформации, определение модуля Юнга для стальной проволоки.
Приборы и принадлежности: прибор, устройство которого описано в разделе описание прибора, микрометр, штангенциркуль, рулетка, набор грузов.
Краткая теория.
Возьмем однородный стержень и приложим к его основаниям А и В растягивающие или сжимающие силы F. Мысленно проведем произвольное сечение С, перпендикулярное к оси стержня. Для равновесия стержня АС необходимо, чтобы на его нижнее основание С действовала сила F1=F. Такая сила возникает потому, что нижняя часть стержня деформирована и действует на нижнюю с силой, равной F1 и противоположно направленной.
Такие силы действуют в любом поперечном сечении растянутого или сжатого стержня. Таким образом, деформация стержня связана с возникновением упругих сил, с которыми каждая часть стержня действует на другую, с которой она граничит. В рассматриваемом случае напряжение перпендикулярно поперечному сечению стержня. Если стержень растянуть, то это напряжение и определяется выражением
![]() ,
(1)
,
(1)
где S – площадь поперечного сечения стержня. Если же стержень сжат, то напряжение называется давлением и численно определяется по формуле
![]() .
(2)
.
(2)
Давление можно рассматривать как отрицательное натяжение и наоборот, то есть
P= - T.
Пусть l0
– длина недеформированного стержня.
После приложения силы F
его длина получает приращение
![]() l
и делается равной l=l0+
l
и делается равной l=l0+![]() l.
Отношение
l.
Отношение
![]()
называется относительным удлинением стержня. Закон Гука для деформации растяжения или сжатия стержней и записывается как
![]() и
и
![]()
Здесь E – постоянная, зависящая только от материала стержня и его физического состояния. Она называется модулем Юнга и выражается формулой
![]() (3)
(3)
Из формулы (3) видно, что модуль Юнга равен такому натяжению, при котором длина стержня удваивается, то есть
![]() при
при
![]() .
.
Методика определения модуля Юнга стальной проволоки.
Для определения
модуля Юнга стальной проволоки необходимо
знать результирующую массу установленных
для растяжения проволоки грузов и
измерить удлинение
![]() l
проволоки при ее растяжении. Удлинение
l
проволоки при ее растяжении. Удлинение
![]() в приборе находят с помощью индикатора
часового типа. В начальном состоянии,
когда поволока только выпрямлена грузом
P0, необходимо
вращением оправы индикатора установить
нулевое положение стрелки прибора(N0).
После подвешивания к проволоке груза
массы m проволока растянется
на величину
в приборе находят с помощью индикатора
часового типа. В начальном состоянии,
когда поволока только выпрямлена грузом
P0, необходимо
вращением оправы индикатора установить
нулевое положение стрелки прибора(N0).
После подвешивания к проволоке груза
массы m проволока растянется
на величину
![]() .
Здесь a – расстояние от
оси вращения рычага r до
щупа микрометра; b –
расстояние от щупа микрометра до
исследуемой проволоки (a=104
мм; b=25 мм). Рычаг к опустится,
и стрелка часового индикатора покажет
величину перемещения рычага
.
Здесь a – расстояние от
оси вращения рычага r до
щупа микрометра; b –
расстояние от щупа микрометра до
исследуемой проволоки (a=104
мм; b=25 мм). Рычаг к опустится,
и стрелка часового индикатора покажет
величину перемещения рычага
![]() в месте нахождения щупа индикатора. На
рисунке показано взаимное расположение
рычага r, часового индикатора
ИЧ – 10 и цилиндра d с
проволокой L. При растяжении
проволоки и опускании рычага r
величину удлинения поволоки
в месте нахождения щупа индикатора. На
рисунке показано взаимное расположение
рычага r, часового индикатора
ИЧ – 10 и цилиндра d с
проволокой L. При растяжении
проволоки и опускании рычага r
величину удлинения поволоки
![]() можно найти, рассматривая два подобных
треугольника
можно найти, рассматривая два подобных
треугольника
![]() .
(4)
.
(4)
Подставив
выражение (4) для
![]() и выразив площадь поперечного сечения
проволоки как
и выразив площадь поперечного сечения
проволоки как
![]() ,
,
где D – диаметр проволоки, получим окончательную формулу для определения модуля Юнга
![]() ,
(5)
,
(5)
где F=mg – величина растягивающего груза; m – масса груза; g – ускорение свободного падения g=9.8 м/с2.
|
№ |
F=mg (H) |
N0 (мм) |
N1 (мм) |
N1-N0 (мм) |
l0 (мм) |
D (мм) |
(мм) |
Е (Н/м2) |
T(H/м2) |
Егр (Н/м2) |
|
1 |
1,029 |
0 |
0,03 |
0,03 |
750 |
0,54 |
0,04 |
9,06*1010 |
4,5*106 |
1,5*1011 |
|
2 |
2,058 |
0 |
0,06 |
0,06 |
750 |
0,54 |
0,07 |
9,06*1010 |
9,0*106 |
|
|
3 |
3,087 |
0 |
0,09 |
0,09 |
750 |
0,54 |
0,11 |
9,06*1010 |
13,5*106 |
|
|
4 |
4,116 |
0 |
0,12 |
0,12 |
750 |
0,54 |
0,15 |
9,06*1010 |
18,0*106 |
|
|
5 |
5,145 |
0 |
0,15 |
0,15 |
750 |
0,54 |
0,19 |
9,06*1010 |
22,5*106 |
|
|
6 |
6,174 |
0 |
0,18 |
0,18 |
750 |
0,54 |
0,22 |
9,06*1010 |
27,0*106 |
T(106)(Н/м2)
![]()
![]() (10-5)(м)
(10-5)(м)
Метод наименьших квадратов:
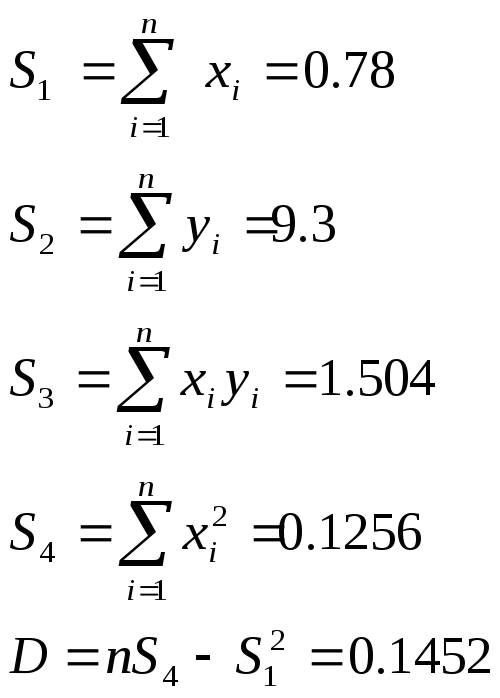
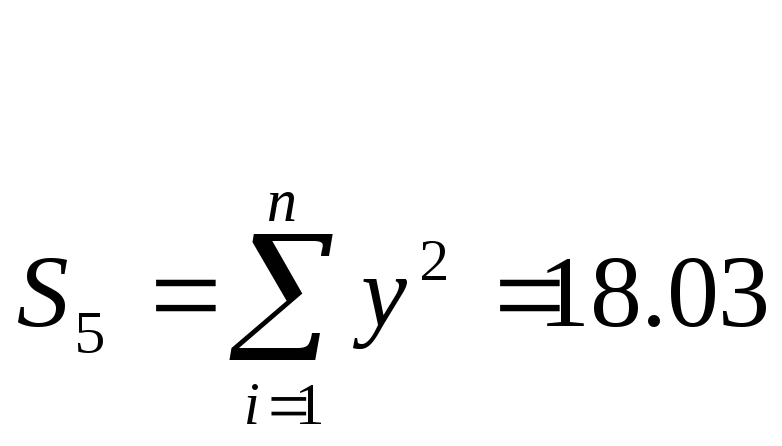

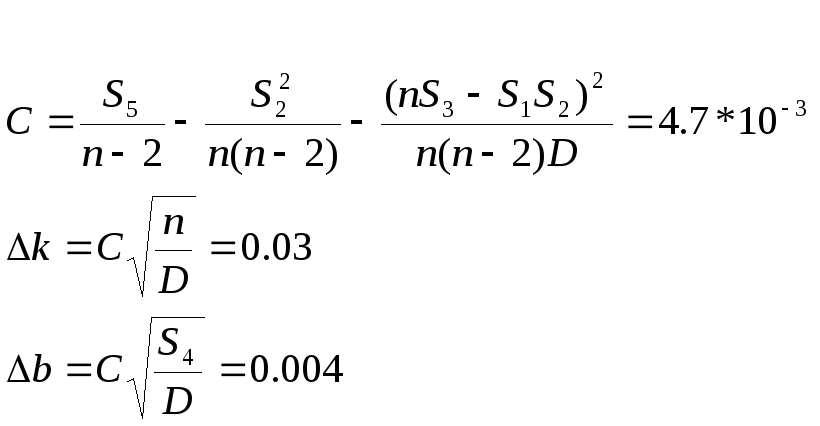
Вывод: Мы ознакомились с одним из методов регистрации величины растяжения стальной проволоки при изучении упругой деформации, определения модуля Юнга для стальной проволоки.
В ходе лабораторной работы, были проведены измерения рассчитанные
