
- •1. Задачи, приводящие к понятию производной, о касательной, о скорости, касательной и нормали.
- •2. Общее определение производной. Различные обозначения.
- •3. Зависимость между непрерывностью и дифф. П-ры непрерывных ф-й.
- •4. Основные правила дифференцирования.
- •5. Производная сложной функции.
- •6. Неявная функция и ее дифференцирование.
- •7. Дифференцирование сложной показат ф-ии. Метод логариф дифф.
- •8. Обратная функция и ее дифференцирование, тригоном.
- •9. Параметрическое задание ф-ии.
- •10. Дифференциал.
- •11. Теоремы ролля, лагранжа, коши. Геометрическое истолкование.
- •12. Возрастание и убывание ф-ии.
- •13. Экстремумы функций.
- •14. Выпуклость и вогнутость ф-ии.
- •15. Исследование ф-и с помощью первой и второй. Общая схема.
- •16. Точки разрыва функции. Асимптоты.
- •17. Комплексные числа.
- •18. Тригонометр форма. Возведение в степень и корень.
- •19. Формула эйлера. Показательная форма.
- •20. Первообразная, неопределнный, св-ва.
- •21. Основные методы интегрирования.
- •22. Интегрирование по частям.
- •23. Рациональные дроби.
- •24. Разложение рацональной дроби. Метод неопределенных коэфф-в.
- •26. Интегрирование простейших иррациональностей.
- •28. Универсальная тригонометрическая подстановка.
- •27. Интегрирование тригонометрических ф-й
- •29. Понятие о неберущихся интегралов.
- •30. Определенный интеграл. Понятия и определения.
- •31. Вычисление определнного интеграла. Формула нбютона – лейбница.
- •32. О.И. С переменным верхним пределом.
- •33. Геометрический и физический смысл о.И.
- •34. Св-ва о.И. Теорема о среднем.
- •35. Инт по частям и замена в ои.
- •36. Несобственные интегралы.
- •37. Геометрическое и физическое приложения ои.
- •38. Ф-я нескольких переменных. Область опред, линии уровня.
- •39. Частное и полное приращение. 1 порядка.
- •41. Производная по направлению. Градиент.
- •42. Чп высших порядков.
- •43. Макс и мин ф-и 2 переменн. Наиб и наим значения.
28. Универсальная тригонометрическая подстановка.
. Переход
в подынтегральной функции к переменной
![]() преобразуетR(sinx,cosx) в функцию,
рационально зависящую отt;
методы интегрирования таких функций
рассмотрены в предыдущем разделе.
Выразимsinx,cosx,dxчерезt:
преобразуетR(sinx,cosx) в функцию,
рационально зависящую отt;
методы интегрирования таких функций
рассмотрены в предыдущем разделе.
Выразимsinx,cosx,dxчерезt: (делим на
(делим на![]() )
)![]() ;
; (делим на
(делим на![]() )
)![]() .
В результате все компоненты подынтегральной
функции выражаются через функции,
рационально зависящие отt.
Пример:
.
В результате все компоненты подынтегральной
функции выражаются через функции,
рационально зависящие отt.
Пример:
![]()

![]()
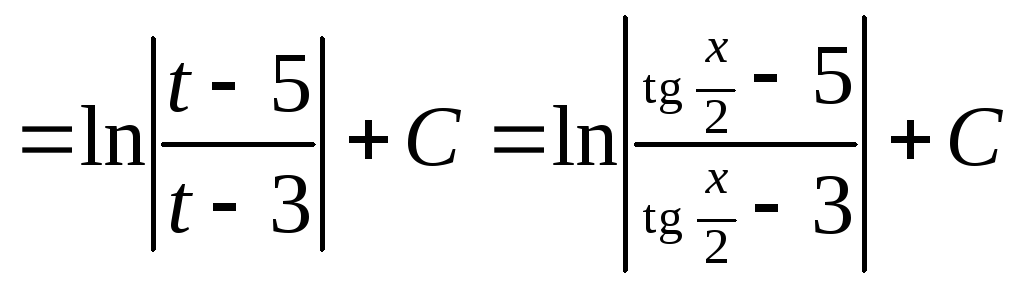 .
.
Универсальная
тригонометрическая подстановка всегда
рационализирует подынтегральную
функцию, с её помощью легко берутся
интегралы вида
![]() (a,b,c- постоянные);
однако часто она приводит к очень
громоздким рациональным дробям, у
которых, в частности, практически
невозможно найти корни знаменателя.
Поэтому при возможности применяются
частные подстановки, которые тоже
рационализируют подынтегральную функцию
и приводят к менее сложным дробям.
(a,b,c- постоянные);
однако часто она приводит к очень
громоздким рациональным дробям, у
которых, в частности, практически
невозможно найти корни знаменателя.
Поэтому при возможности применяются
частные подстановки, которые тоже
рационализируют подынтегральную функцию
и приводят к менее сложным дробям.
Частные тригонометрические подстановки.
1. Подынтегральная функция нечётна относительно sin x, т.е.R(-sinx,cosx) =
= - R(sinx,cosx). В этом случае применима подстановкаt=cosx.
2. Подынтегральная функция нечётна относительно cosx, т.е.R(sinx, -cosx) =
= - R(sinx,cosx). В этом случае применима подстановкаt=sinx.
3. Подынтегральная функция чётна относительно sinxиcosx, т.е.
R(-sin
x,
-cos x)
= R(sin
x,
cos x).
В этом случае применима подстановкаt=tgx(илиt=ctgx,
причём ответить на вопрос, что лучше,
может только проба). Выражения sinx,cosxиdxчерезtgx:![]() .
.
27. Интегрирование тригонометрических ф-й
Интеграл вида
![]() .ЗдесьR– обозначение
некоторой рациональной функции от
переменныхsinxиcosx.
Интегралы этого вида вычисляются с
помощью подстановки t=tg(x/2).
Эта подстановка позволяет преобразовать
тригонометрическую функцию в рациональную.
.ЗдесьR– обозначение
некоторой рациональной функции от
переменныхsinxиcosx.
Интегралы этого вида вычисляются с
помощью подстановки t=tg(x/2).
Эта подстановка позволяет преобразовать
тригонометрическую функцию в рациональную.
![]() ,
,
![]() Тогда
Тогда
![]() Таким образом:
Таким образом:
![]() Описанное выше преобразование называетсяуниверсальной тригонометрической
подстановкой.
Описанное выше преобразование называетсяуниверсальной тригонометрической
подстановкой.
Пример.
![]()
Несомненным достоинством этой подстановки является то, что с ее помощью всегда можно преобразовать тригонометрическую функцию в рациональную и вычислить соответствующий интеграл. К недостаткам можно отнести то, что при преобразовании может получиться достаточно сложная рациональная функция, интегрирование которой займет много времени и сил.
Однако при невозможности применить более рациональную замену переменной этот метод является единственно результативным.
Интеграл вида
![]() если
функция R является
нечетной относительно cosx.
если
функция R является
нечетной относительно cosx.
Несмотря на возможность вычисления такого интеграла с помощью универсальной тригонометрической подстановки, рациональнее применить подстановку t = sinx.
![]()
Функция
![]() может
содержатьcosxтолько в
четных степенях, а следовательно, может
быть преобразована в рациональную
функцию относительноsinx.
может
содержатьcosxтолько в
четных степенях, а следовательно, может
быть преобразована в рациональную
функцию относительноsinx.
![]()
Вообще говоря, для применения этого метода необходима только нечетность функции относительно косинуса, а степень синуса, входящего в функцию может быть любой, как целой, так и дробной.
Интеграл вида
![]() если
функция R является
нечетной относительно sinx.
если
функция R является
нечетной относительно sinx.
По аналогии с рассмотренным выше случаем делается подстановка t = cosx.
Тогда
![]()
Интеграл вида
![]() функция
R четная относительно
sinx и cosx.
функция
R четная относительно
sinx и cosx.
Для преобразования функции Rв рациональную используется подстановка
t
= tgx.Тогда
![]()
Интеграл произведения синусов и косинусов различных аргументов.
В зависимости от типа произведения применятся одна из трех формул:
![]()
![]()
![]()
