
Вариант 7.
Пусть
 выборка из генеральной совокупности,
распределенной по закону с плотностью
выборка из генеральной совокупности,
распределенной по закону с плотностью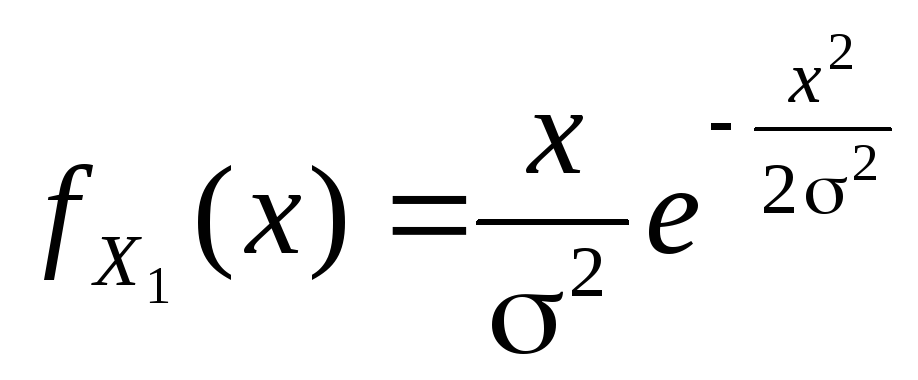 ,
,
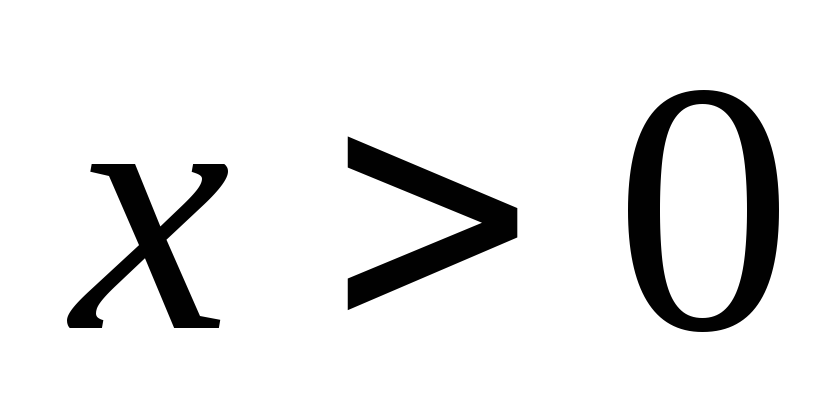 .
. .
Найти оценки параметра
.
Найти оценки параметра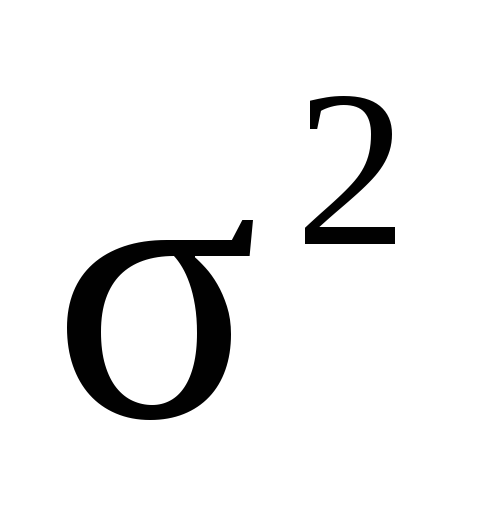 по методу моментов (по любому моменту)
и методу максимального правдоподобия.
Проверить состоятельность и несмещенность
полученных оценок.
по методу моментов (по любому моменту)
и методу максимального правдоподобия.
Проверить состоятельность и несмещенность
полученных оценок.Дана выборка
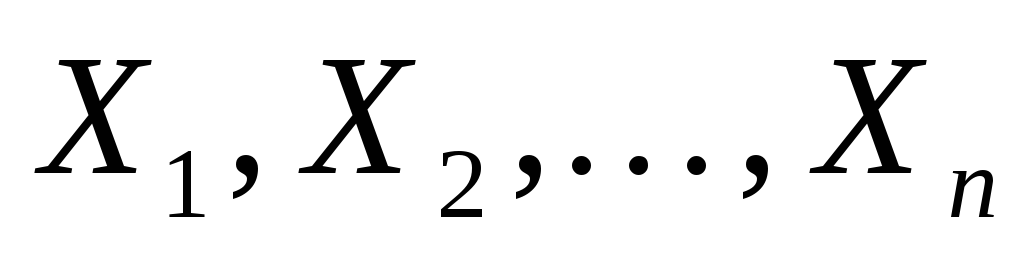 из генеральной совокупности, имеющей
непрерывное распределение с плотностью
из генеральной совокупности, имеющей
непрерывное распределение с плотностью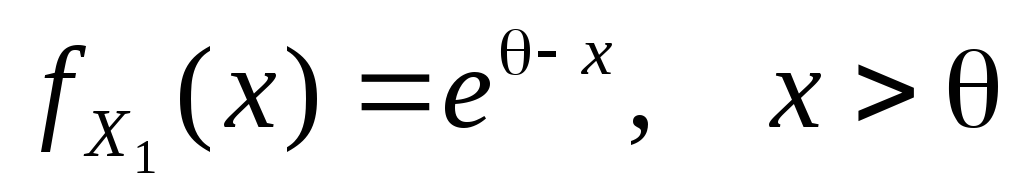 ,
где
,
где - неизвестный параметр. Сравнить при
помощи асимптотического подхода оценки
параметра
- неизвестный параметр. Сравнить при
помощи асимптотического подхода оценки
параметра метода моментов, найденные по первому
и второму моментам.
метода моментов, найденные по первому
и второму моментам.Пусть
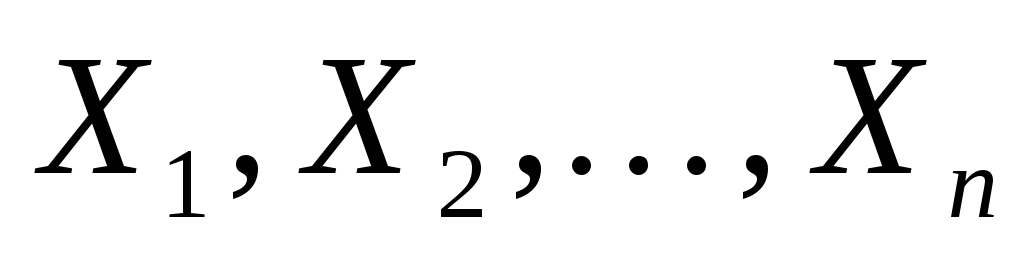 выборка из генеральной совокупности,
имеющей гамма распределение:
выборка из генеральной совокупности,
имеющей гамма распределение:
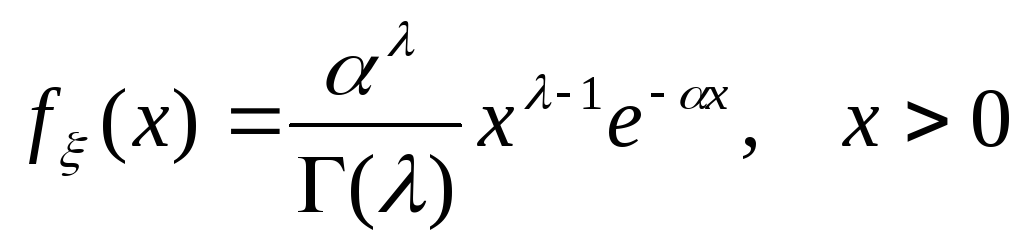 ,
с неизвестным параметром
,
с неизвестным параметром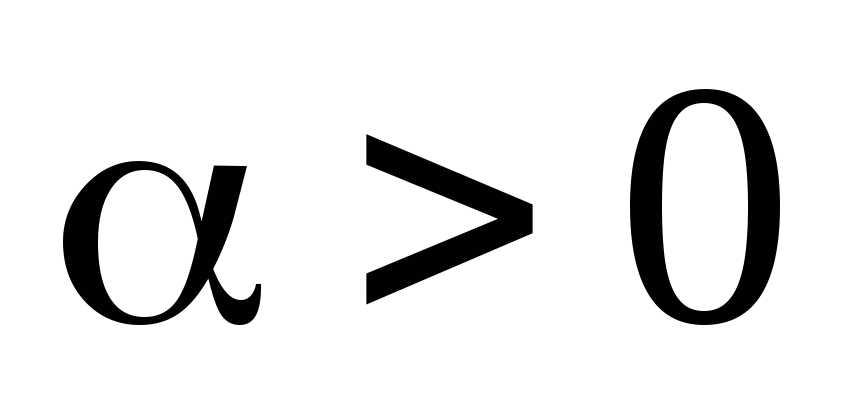 и известным параметром
и известным параметром .
Проверить эффективность оценки
.
Проверить эффективность оценки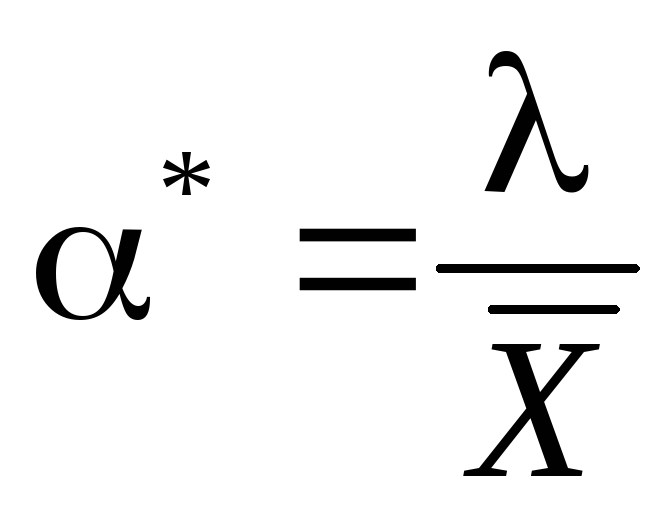 (Здесь
(Здесь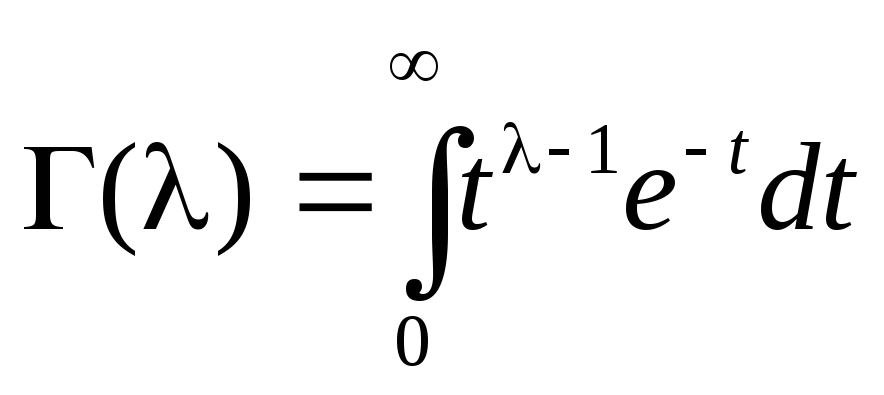 -
гамма функция,
-
гамма функция, ,
,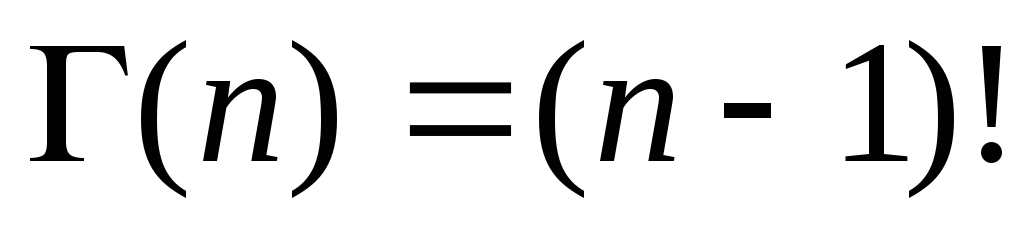 ,
, ).
).Имеется выборка из
 значений нормальной случайной величины
значений нормальной случайной величины (Приложение 1, таблица 1, N - номер варианта).
Построить точные доверительные интервалы
для параметров нормальной случайной
величины
(Приложение 1, таблица 1, N - номер варианта).
Построить точные доверительные интервалы
для параметров нормальной случайной
величины ,
соответствующие доверительной
вероятности
,
соответствующие доверительной
вероятности .
.Какова вероятность того, что среднеарифметическое из n = 9 измерений для выборки из нормальной совокупности отличается от математического ожидания этой совокупности не более, чем на = 0,2, если известна дисперсия совокупности
 ?
?
Вариант 8.
Пусть
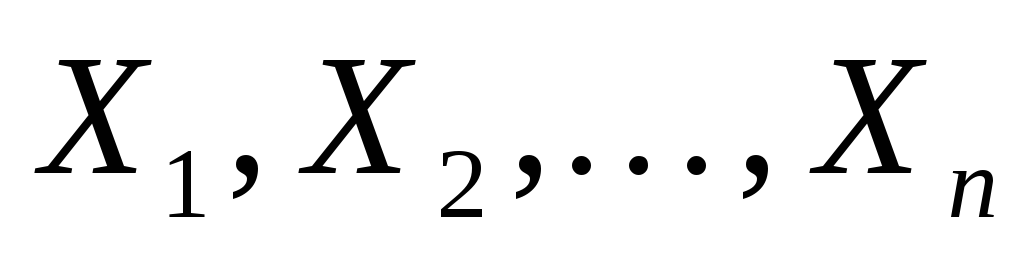 выборка из генеральной совокупности,
распределенной по закону с плотностью
выборка из генеральной совокупности,
распределенной по закону с плотностью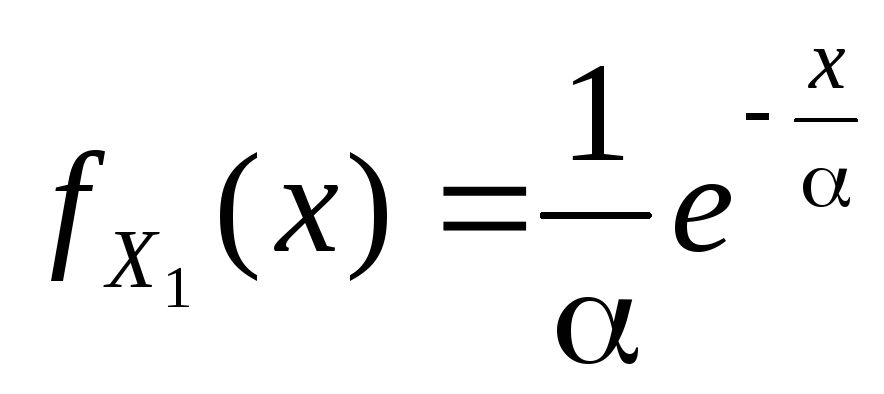 ,
,
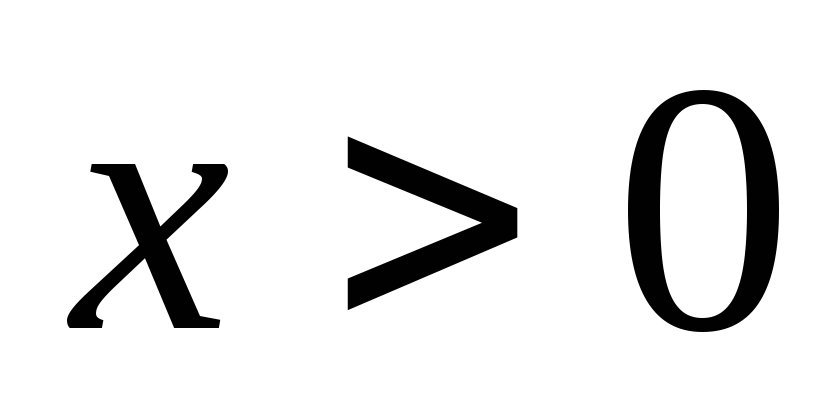 .
.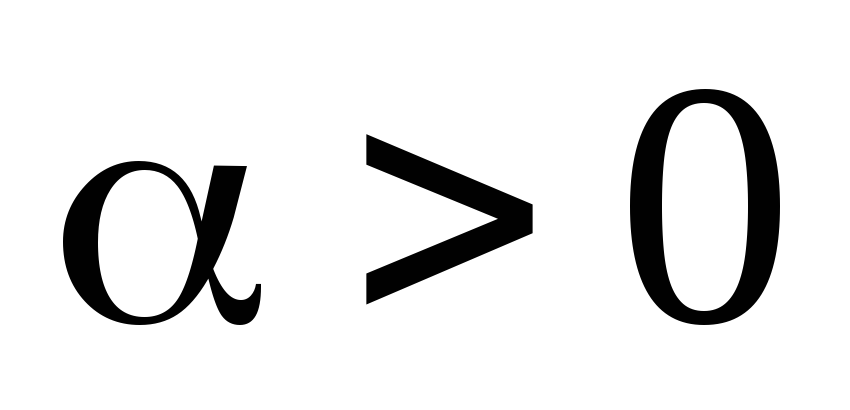 .
Найти оценки параметра
.
Найти оценки параметра по методу моментов (по любому моменту)
и методу максимального правдоподобия.
Проверить состоятельность и несмещенность
полученных оценок.
по методу моментов (по любому моменту)
и методу максимального правдоподобия.
Проверить состоятельность и несмещенность
полученных оценок.Дана выборка
 из генеральной совокупности, имеющей
плотность распределения
из генеральной совокупности, имеющей
плотность распределения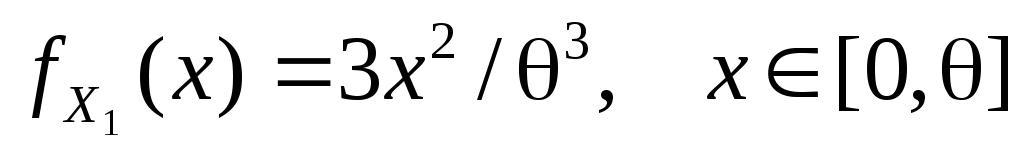 ,
с неизвестным параметром
,
с неизвестным параметром .
Сравнить при помощи асимптотического
подхода оценки параметра
.
Сравнить при помощи асимптотического
подхода оценки параметра метода моментов, найденные по первому
и второму моментам.
метода моментов, найденные по первому
и второму моментам.Пусть
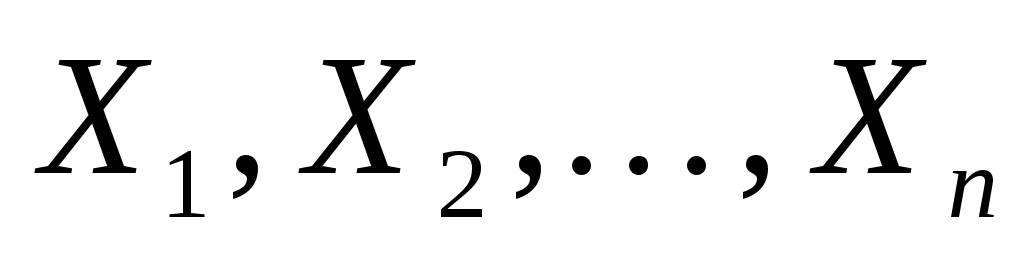 выборка из генеральной совокупности,
имеющей плотность распределения
выборка из генеральной совокупности,
имеющей плотность распределения
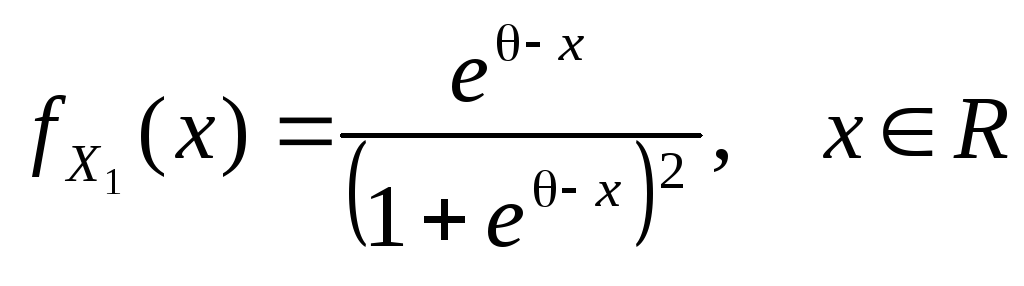 ,
с неизвестным параметром
,
с неизвестным параметром .
Проверить эффективность оценки
.
Проверить эффективность оценки .
.Имеется выборка из
 значений нормальной случайной величины
значений нормальной случайной величины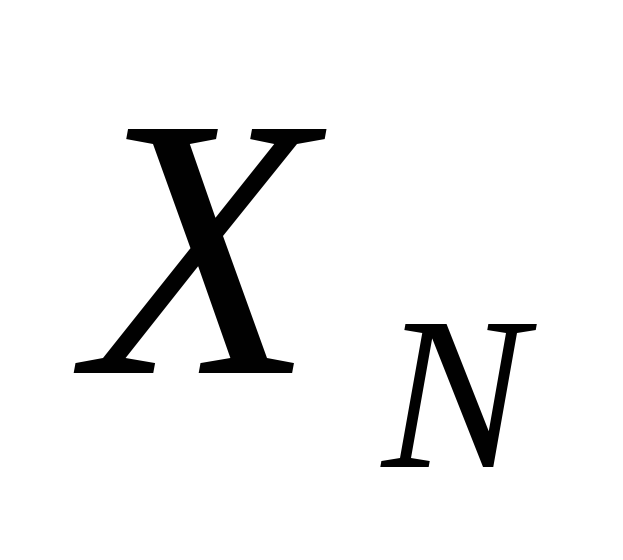 (Приложение 1, таблица 1, N - номер варианта).
Построить точные доверительные интервалы
для параметров нормальной случайной
величины
(Приложение 1, таблица 1, N - номер варианта).
Построить точные доверительные интервалы
для параметров нормальной случайной
величины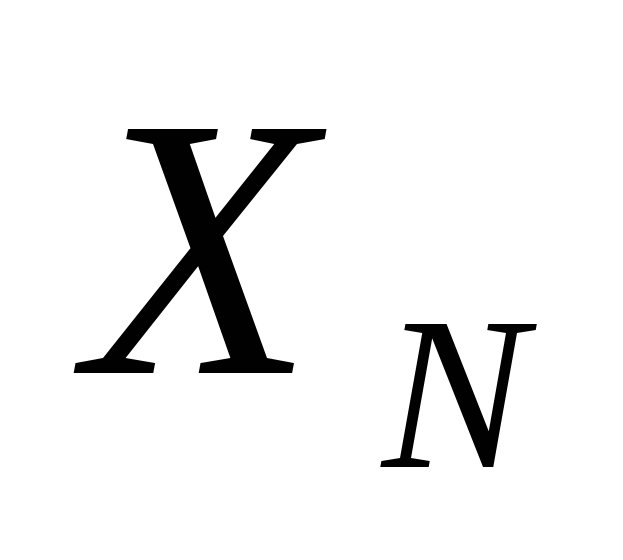 ,
соответствующие доверительной
вероятности
,
соответствующие доверительной
вероятности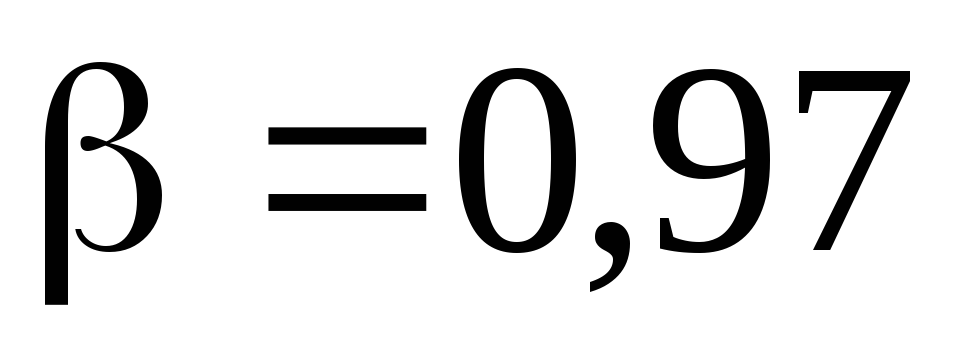 .
.Какова вероятность того, что среднеарифметическое из n = 16 измерений для выборки из нормальной совокупности отличается от математического ожидания этой совокупности не более, чем на = 0,02, если несмещенная выборочная дисперсия
 ?
?
Вариант 9.
Пусть
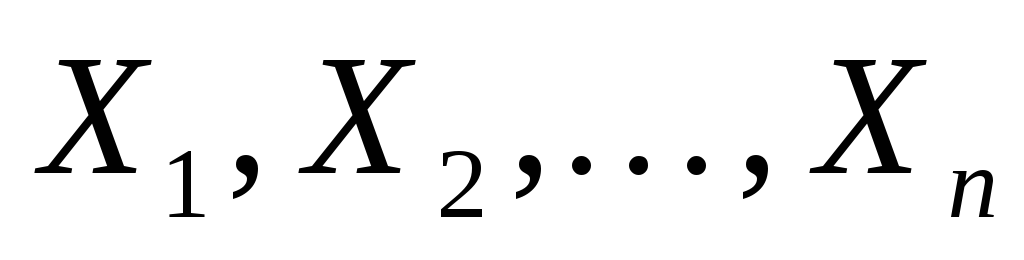 выборка из генеральной совокупности,
имеющей плотность распределения
выборка из генеральной совокупности,
имеющей плотность распределения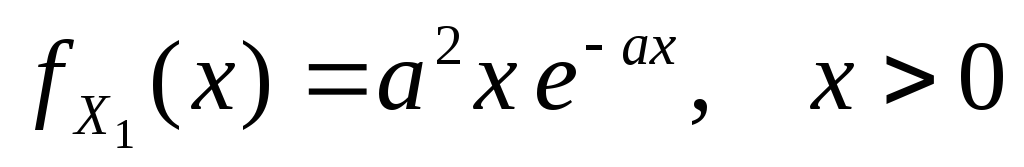 ,
с неизвестным параметром
,
с неизвестным параметром .
Найти оценки параметра
.
Найти оценки параметра по методу моментов (по любому моменту)
и методу максимального правдоподобия.
Проверить состоятельность и несмещенность
полученных оценок.
по методу моментов (по любому моменту)
и методу максимального правдоподобия.
Проверить состоятельность и несмещенность
полученных оценок.Дана выборка
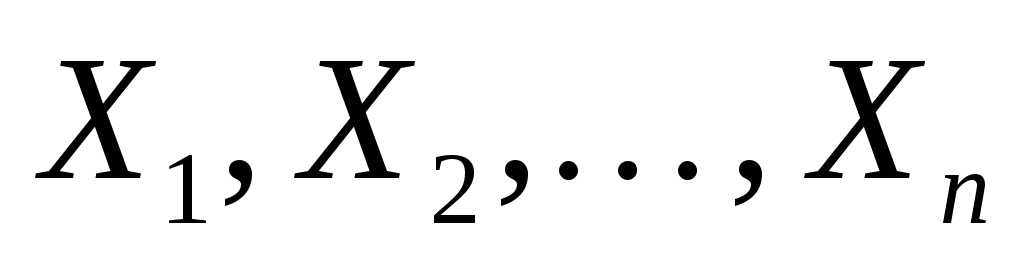 из генеральной совокупности, имеющей
плотность распределения
из генеральной совокупности, имеющей
плотность распределения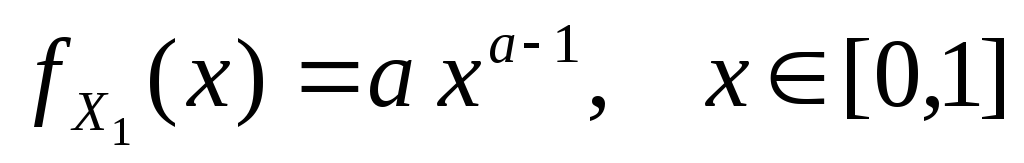 ,
с неизвестным параметром
,
с неизвестным параметром .
Сравнить при помощи асимптотического
подхода оценки параметра
.
Сравнить при помощи асимптотического
подхода оценки параметра метода моментов, найденные по первому
и второму моментам.
метода моментов, найденные по первому
и второму моментам.Пусть
 выборка из генеральной совокупности,
имеющей плотность распределения
выборка из генеральной совокупности,
имеющей плотность распределения ,
с неизвестным параметром
,
с неизвестным параметром и известным параметром
и известным параметром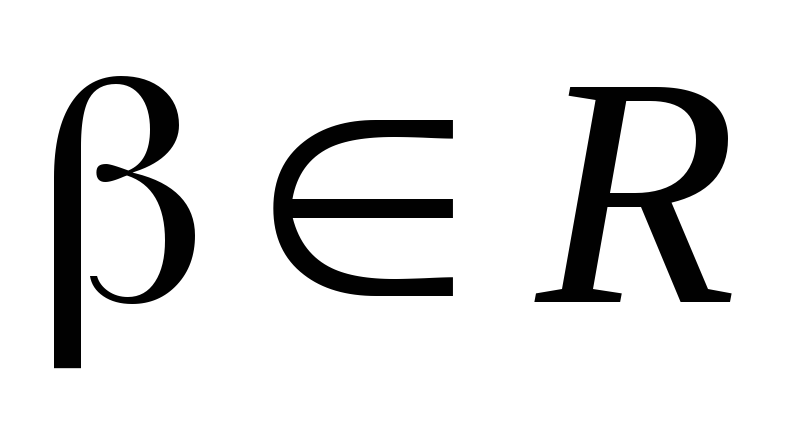 .
Проверить эффективность оценки
.
Проверить эффективность оценки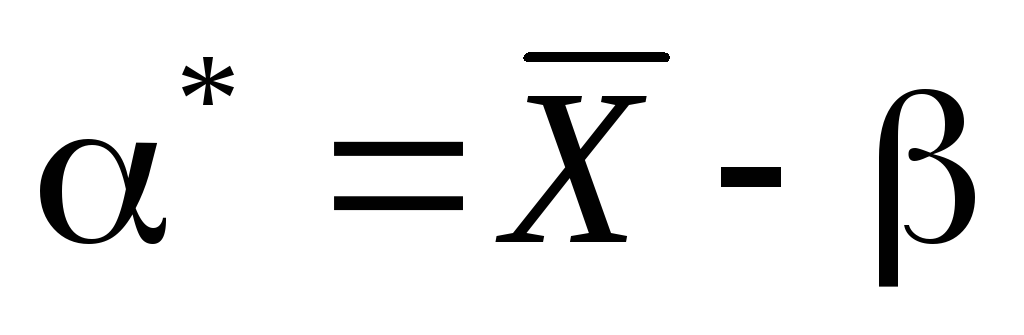 .
.Имеется выборка из
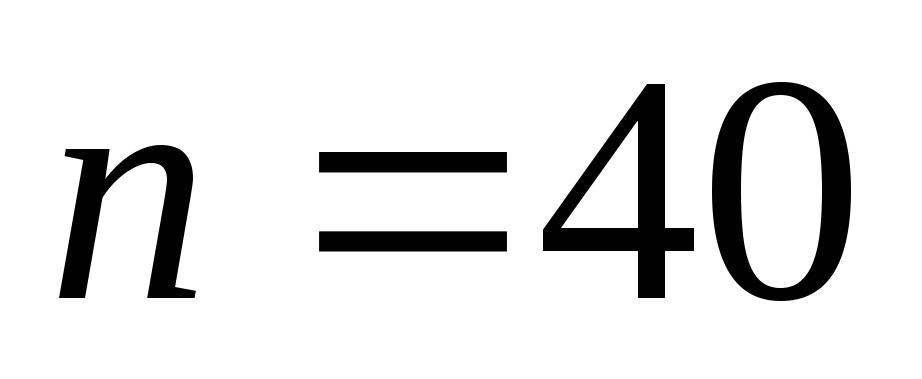 значений нормальной случайной величины
значений нормальной случайной величины (Приложение 1, таблица 1, N - номер варианта).
Построить точные доверительные интервалы
для параметров нормальной случайной
величины
(Приложение 1, таблица 1, N - номер варианта).
Построить точные доверительные интервалы
для параметров нормальной случайной
величины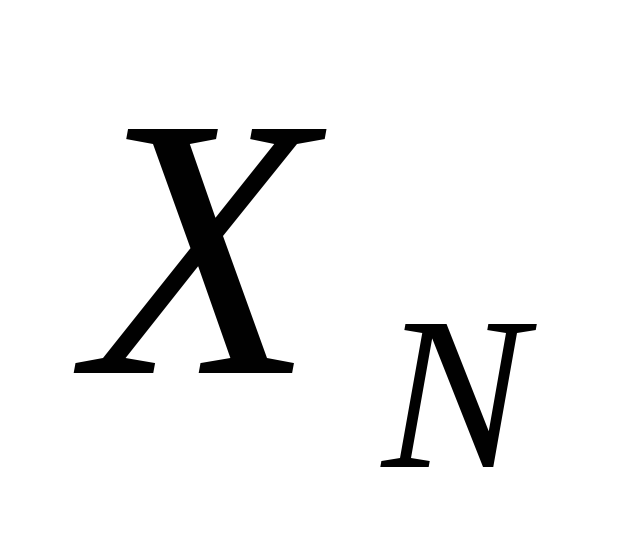 ,
соответствующие доверительной
вероятности
,
соответствующие доверительной
вероятности .
.Какова вероятность того, что среднеарифметическое из n = 16 измерений для выборки из нормальной совокупности отличается от математического ожидания этой совокупности не более, чем на = 0,02, если известна дисперсия совокупности
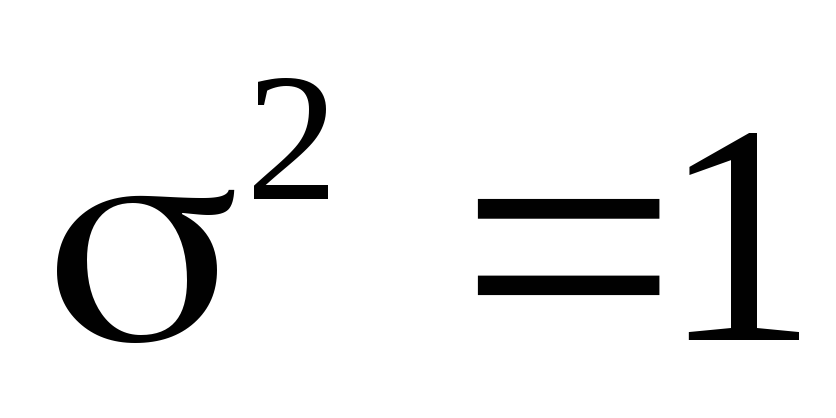 ?
?
Вариант 10.
Пусть
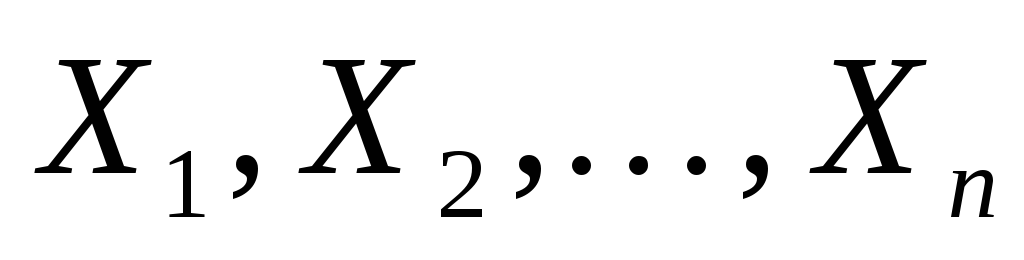 выборка из генеральной совокупности,
имеющей плотность распределения
выборка из генеральной совокупности,
имеющей плотность распределения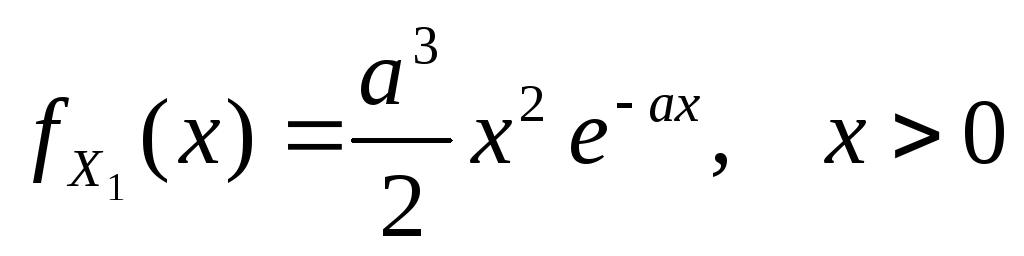 ,
с неизвестным параметром
,
с неизвестным параметром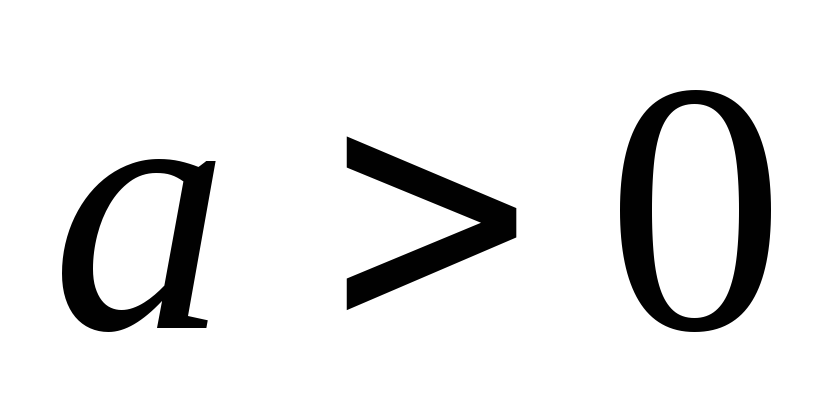 .
Найти оценки параметра
.
Найти оценки параметра по методу моментов (по любому моменту)
и методу максимального правдоподобия.
Проверить состоятельность и несмещенность
полученных оценок.
по методу моментов (по любому моменту)
и методу максимального правдоподобия.
Проверить состоятельность и несмещенность
полученных оценок.Дана выборка
 из генеральной совокупности, имеющей
плотность распределения
из генеральной совокупности, имеющей
плотность распределения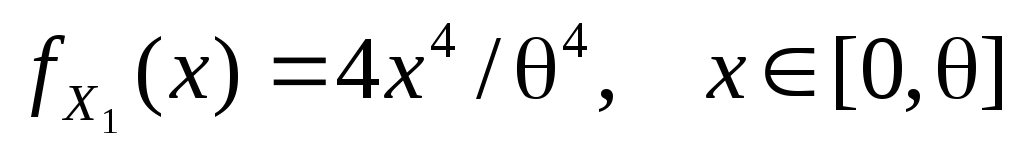 ,
с неизвестным параметром
,
с неизвестным параметром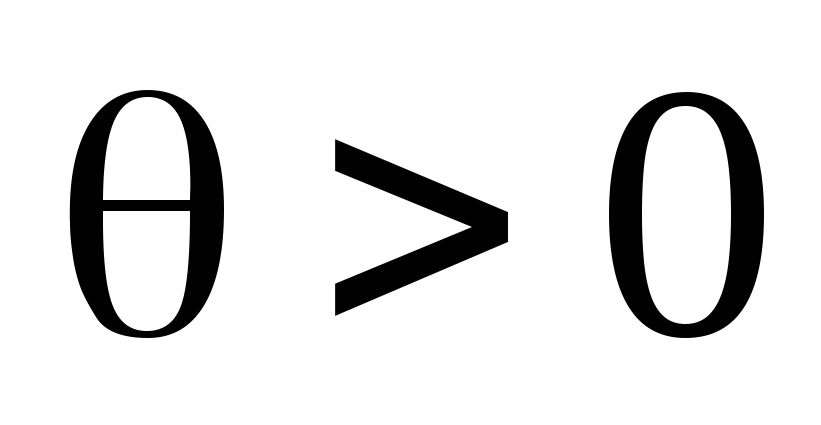 .
Сравнить при помощи асимптотического
подхода оценки параметра
.
Сравнить при помощи асимптотического
подхода оценки параметра метода моментов, найденные по первому
и второму моментам.
метода моментов, найденные по первому
и второму моментам.Пусть
 выборка из генеральной совокупности,
распределенной по показательному
закону с неизвестным параметром
выборка из генеральной совокупности,
распределенной по показательному
закону с неизвестным параметром .
Проверить эффективность оценки
.
Проверить эффективность оценки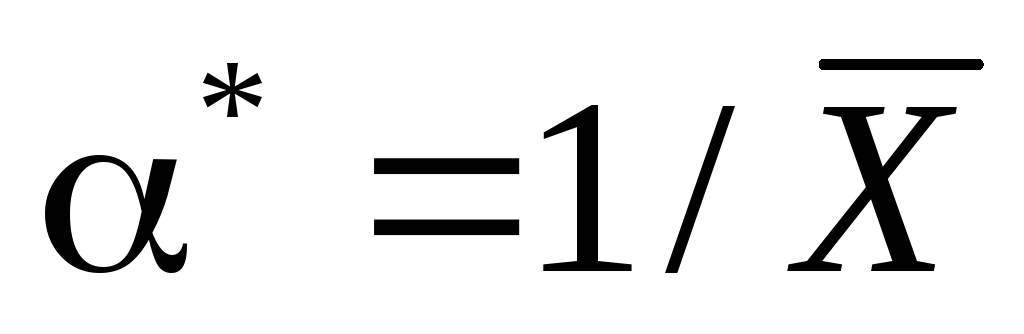 .
.Имеется выборка из
 значений нормальной случайной величины
значений нормальной случайной величины (Приложение 1, таблица 1, N - номер варианта).
Построить точные доверительные интервалы
для параметров нормальной случайной
величины
(Приложение 1, таблица 1, N - номер варианта).
Построить точные доверительные интервалы
для параметров нормальной случайной
величины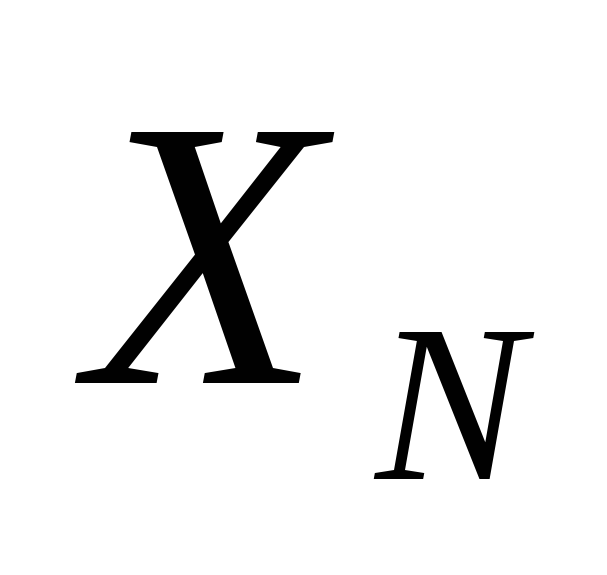 ,
соответствующие доверительной
вероятности
,
соответствующие доверительной
вероятности .
.Какова вероятность того, что среднеарифметическое из n = 16 измерений для выборки из нормальной совокупности отличается от математического ожидания этой совокупности не более, чем на = 0,02, если известна дисперсия совокупности
 ?
?
