
Вариант 1.
Пусть
 выборка из генеральной совокупности,
имеющей непрерывное распределение с
плотностью
выборка из генеральной совокупности,
имеющей непрерывное распределение с
плотностью ,
где
,
где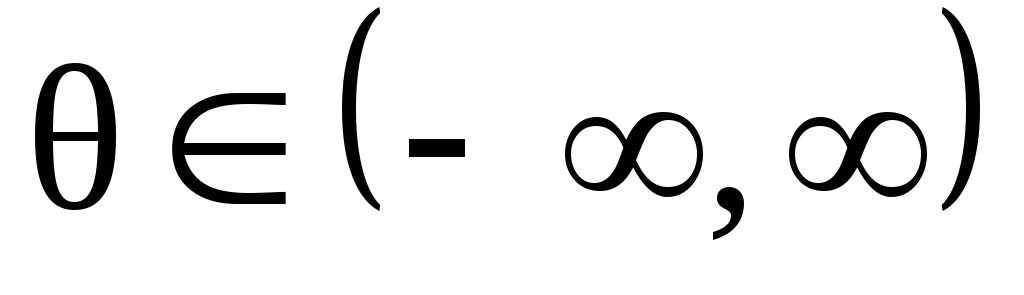 - неизвестный параметр. Найти оценки
параметра
- неизвестный параметр. Найти оценки
параметра метода моментов (по любому моменту) и
метода максимального правдоподобия.
Проверить, является ли полученные
оценки состоятельными и несмещенными.
метода моментов (по любому моменту) и
метода максимального правдоподобия.
Проверить, является ли полученные
оценки состоятельными и несмещенными.Дана выборка
 из генеральной совокупности, имеющей
плотность распределения
из генеральной совокупности, имеющей
плотность распределения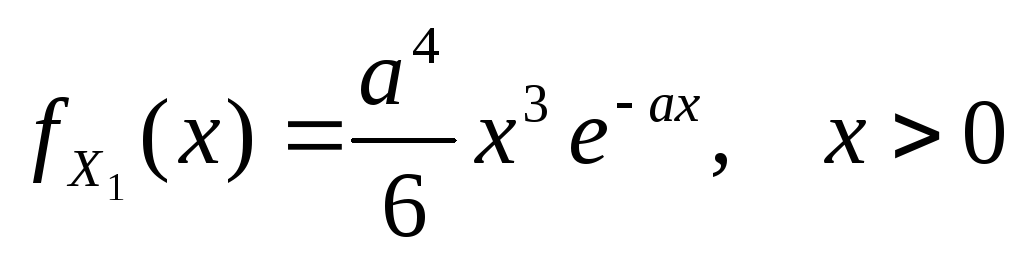 ,
с неизвестным параметром
,
с неизвестным параметром .
Сравнить при помощи асимптотического
подхода оценки параметра
.
Сравнить при помощи асимптотического
подхода оценки параметра метода моментов, найденные по первому
и второму моментам.
метода моментов, найденные по первому
и второму моментам.Пусть
 выборка из генеральной совокупности,
распределенной по нормальному закону
выборка из генеральной совокупности,
распределенной по нормальному закону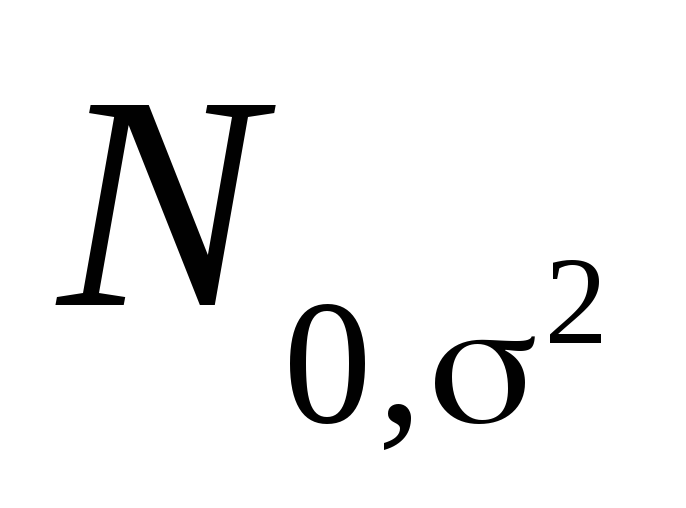 ,
с неизвестным параметром
,
с неизвестным параметром .
Проверить эффективность оценки
.
Проверить эффективность оценки .
.Имеется выборка из
 значений нормальной случайной величины
значений нормальной случайной величины (Приложение 1, таблица 1, N - номер варианта).
Построить точные доверительные интервалы
для параметров нормальной случайной
величины
(Приложение 1, таблица 1, N - номер варианта).
Построить точные доверительные интервалы
для параметров нормальной случайной
величины ,
соответствующие доверительной
вероятности
,
соответствующие доверительной
вероятности .
.Сколько надо произвести измерений, чтобы с вероятностью 0,9 получить абсолютную погрешность оценки математического ожидания нормальной случайной величины не более 0,1, если
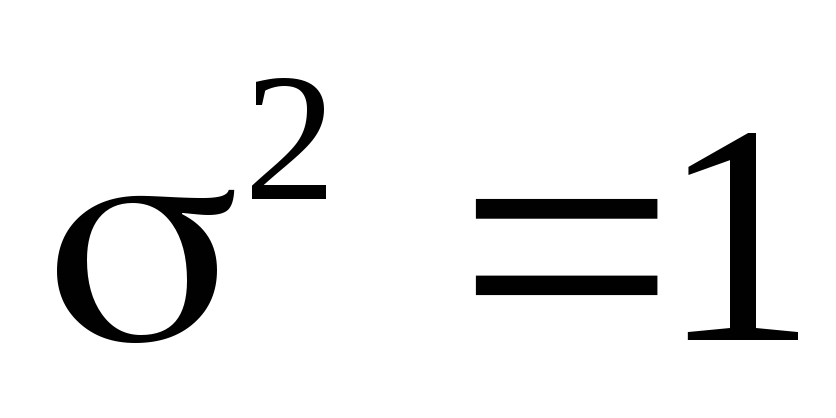 ,
а в качестве оценки используется
выборочное среднее?
,
а в качестве оценки используется
выборочное среднее?
Вариант 2.
Пусть
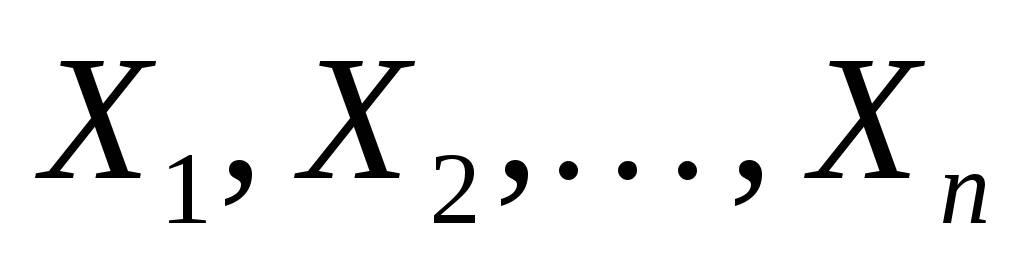 выборка из генеральной совокупности,
имеющей плотность распределения
выборка из генеральной совокупности,
имеющей плотность распределения ,
с неизвестным параметром
,
с неизвестным параметром .
Найти оценки параметра
.
Найти оценки параметра метода моментов (по любому моменту) и
методу максимального правдоподобия.
Проверить состоятельность и несмещенность
полученных оценок.
метода моментов (по любому моменту) и
методу максимального правдоподобия.
Проверить состоятельность и несмещенность
полученных оценок.Дана выборка
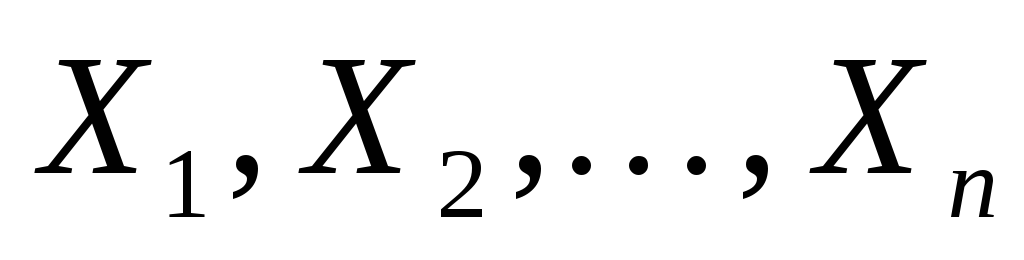 из генеральной совокупности, распределенной
по показательному закону с неизвестным
параметром
из генеральной совокупности, распределенной
по показательному закону с неизвестным
параметром .
Сравнить при помощи асимптотического
подхода оценки параметра
.
Сравнить при помощи асимптотического
подхода оценки параметра метода моментов, найденные по первому
и второму моментам.
метода моментов, найденные по первому
и второму моментам.Пусть
 выборка из генеральной совокупности,
имеющей плотность распределения
выборка из генеральной совокупности,
имеющей плотность распределения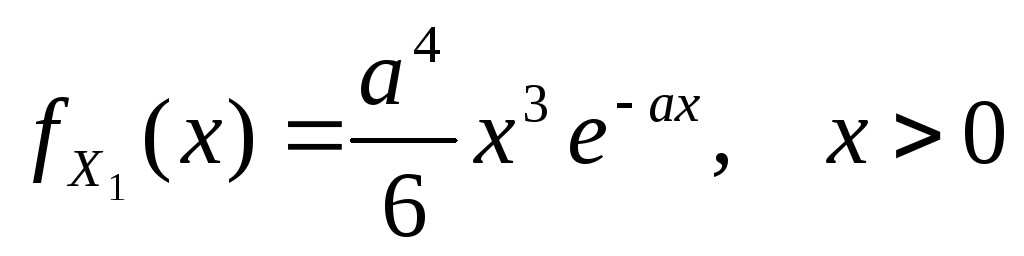 ,
с неизвестным параметром
,
с неизвестным параметром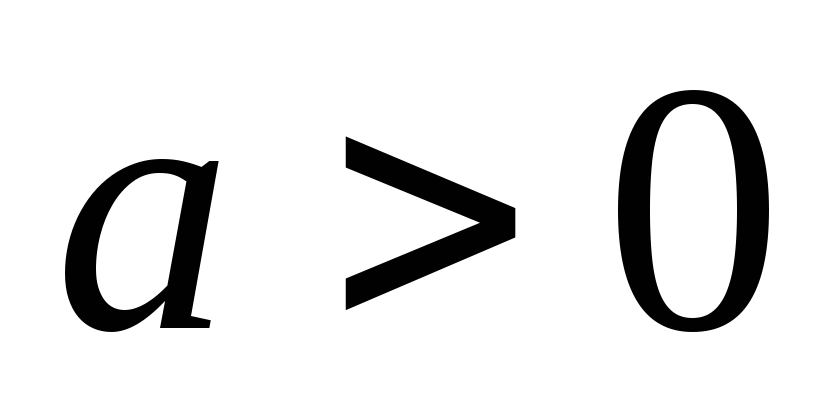 .
Является ли оценка
.
Является ли оценка эффективной оценкой параметра
эффективной оценкой параметра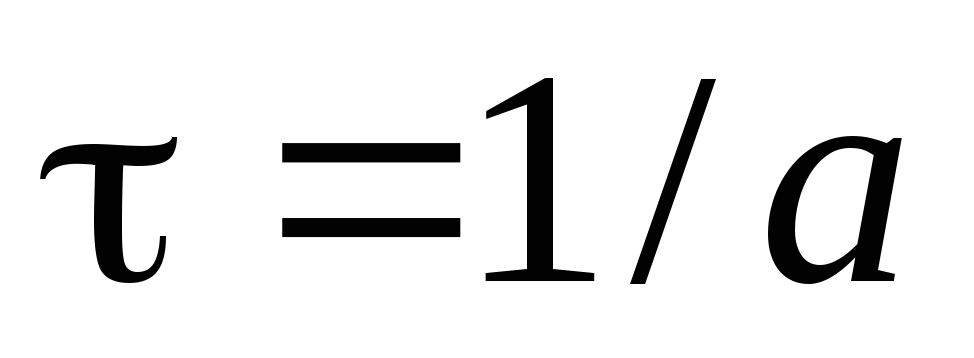 ?
?Имеется выборка из
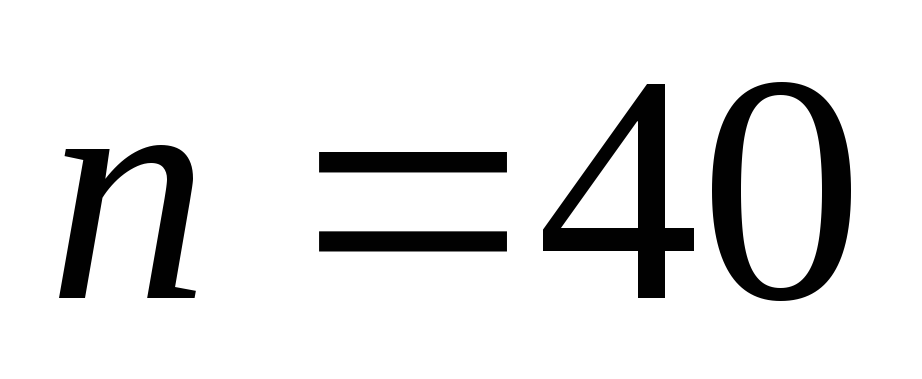 значений нормальной случайной величины
значений нормальной случайной величины (Приложение 1, таблица 1, N - номер варианта).
Построить точные доверительные интервалы
для параметров нормальной случайной
величины
(Приложение 1, таблица 1, N - номер варианта).
Построить точные доверительные интервалы
для параметров нормальной случайной
величины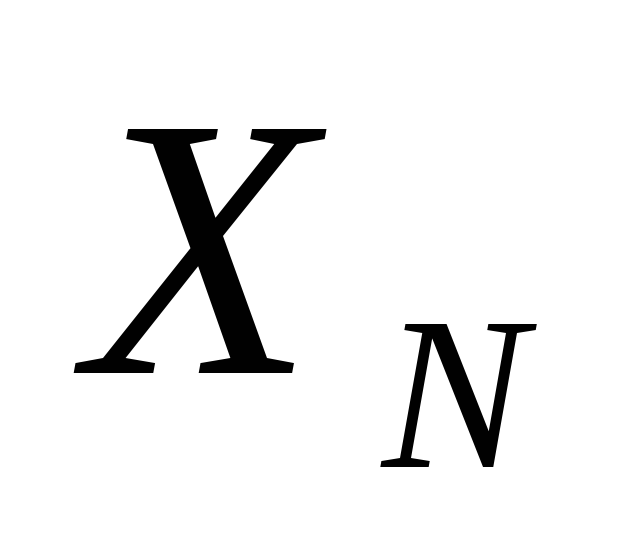 ,
соответствующие доверительной
вероятности
,
соответствующие доверительной
вероятности .
.Сколько надо произвести измерений, чтобы с вероятностью 0,95 получить абсолютную погрешность оценки математического ожидания нормальной случайной величины не более 0,01, если
 ,
а в качестве оценки используется
выборочное среднее?
,
а в качестве оценки используется
выборочное среднее?
Вариант 3.
Пусть
 выборка из генеральной совокупности,
распределенной по закону Бернулли с
неизвестным параметром
выборка из генеральной совокупности,
распределенной по закону Бернулли с
неизвестным параметром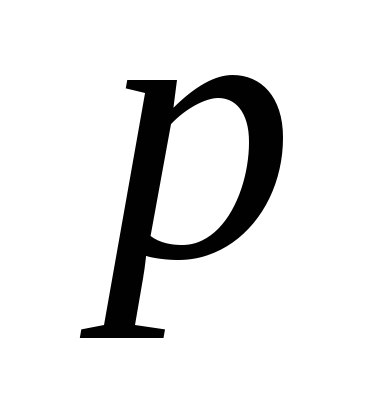 .
Найти оценки параметра метода моментов
(по любому моменту) и метода максимального
правдоподобия. Проверить состоятельность
и несмещенность полученных оценок.
.
Найти оценки параметра метода моментов
(по любому моменту) и метода максимального
правдоподобия. Проверить состоятельность
и несмещенность полученных оценок.Дана выборка
 из генеральной совокупности, имеющей
плотность распределения
из генеральной совокупности, имеющей
плотность распределения ,
с неизвестным параметром
,
с неизвестным параметром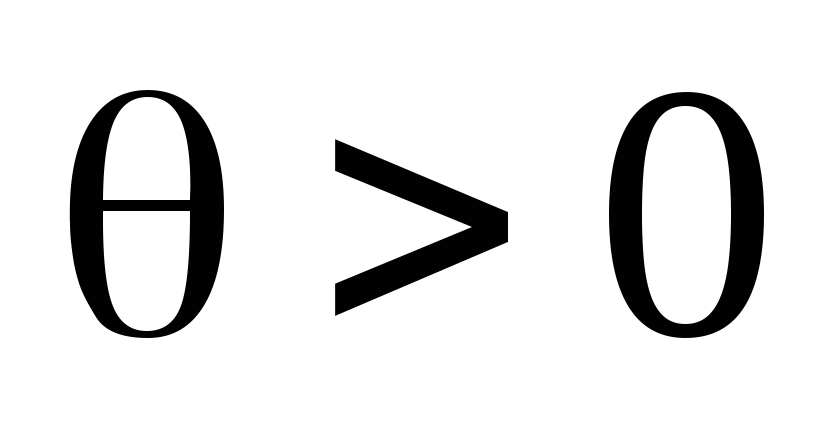 .
Сравнить при помощи асимптотического
подхода оценки параметра
.
Сравнить при помощи асимптотического
подхода оценки параметра метода моментов, найденные по первому
и второму моментам.
метода моментов, найденные по первому
и второму моментам.Пусть
 выборка из генеральной совокупности,
распределенной по нормальному закону
выборка из генеральной совокупности,
распределенной по нормальному закону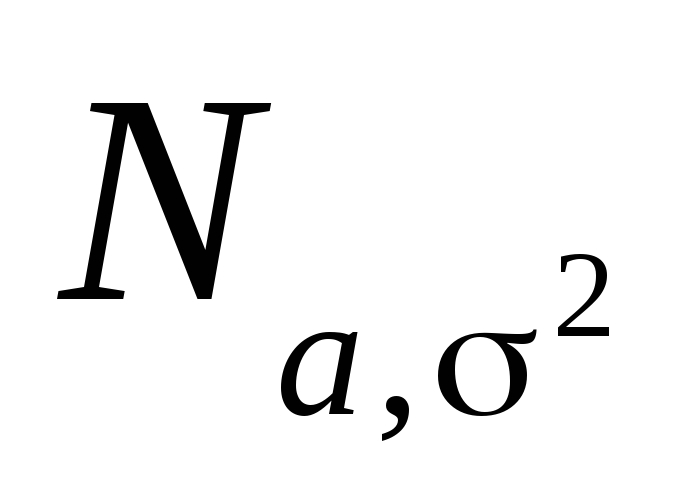 ,
где параметр
,
где параметр неизвестен, а параметр
неизвестен, а параметр известен. Проверить эффективность
оценки
известен. Проверить эффективность
оценки .
.Имеется выборка из
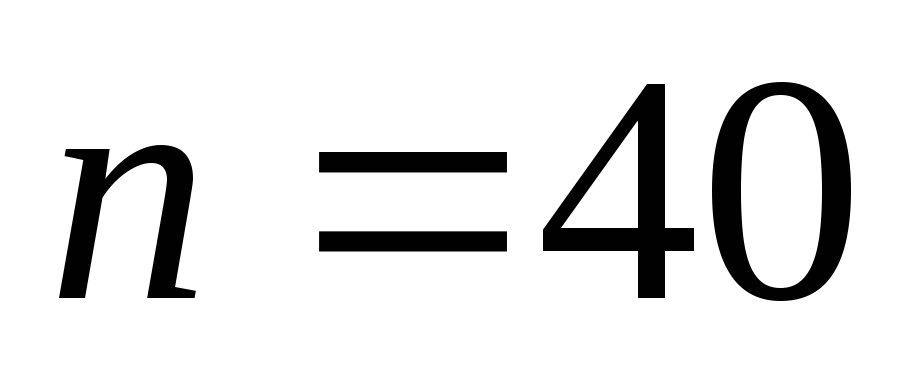 значений нормальной случайной величины
значений нормальной случайной величины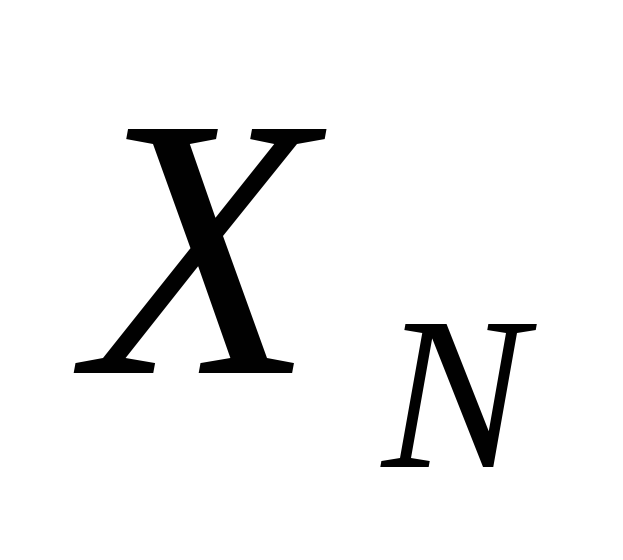 (Приложение 1, таблица 1, N - номер варианта).
Построить точные доверительные интервалы
для параметров нормальной случайной
величины
(Приложение 1, таблица 1, N - номер варианта).
Построить точные доверительные интервалы
для параметров нормальной случайной
величины ,
соответствующие доверительной
вероятности
,
соответствующие доверительной
вероятности .
.Сколько надо произвести измерений, чтобы с вероятностью 0,99 получить абсолютную погрешность оценки математического ожидания нормальной случайной величины не более 0,02, если
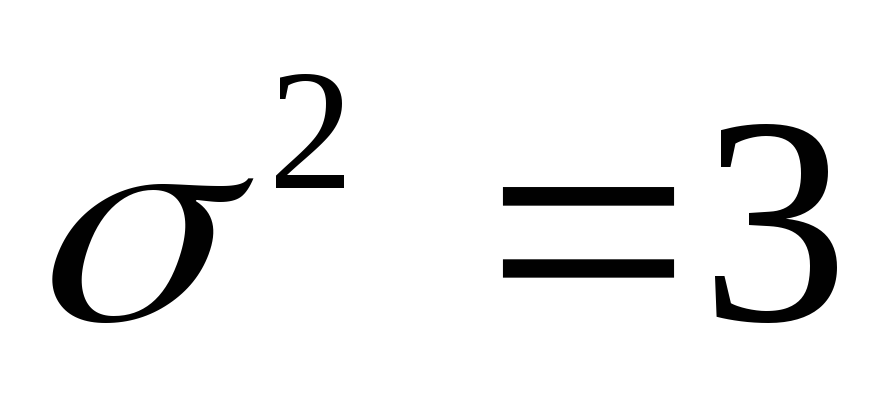 ,
а в качестве оценки используется
выборочное среднее?
,
а в качестве оценки используется
выборочное среднее?
