ЛАБОРАТОРНАЯ РАБОТА РЕГРЕССИО

ЛАБОРАТОРНАЯ РАБОТА

Регрессионный анализ парных наблюдений

Цель работы:

Оценка параметров уравнения регрессии.

Задание.

Имеется выборка значений совместно наблюдаемых величин и (Приложение 2).

Требуется:

1. Отобразить графически поле наблюдаемых значений величин и .

2. Методом наименьших квадратов найти оценки параметров уравнения линейной и квадратичной регрессии на . Изобразить полученные зависимости на фоне корреляционного поля.

3. Проверить значимость коэффициентов уравнения регрессии (используя достигнутый уровень значимости), в предположении, что остатки независимые нормальные случайные величины с одинаковой дисперсией.

4. Сравнить модели, используя значения оценок остаточной дисперсии и коэффициента детерминации, а также полученные (достигнутые) уровни значимости коэффициентов моделей, выбрать одну из них (обосновать выбор).

5. Определить границы доверительного интервала для средних значений 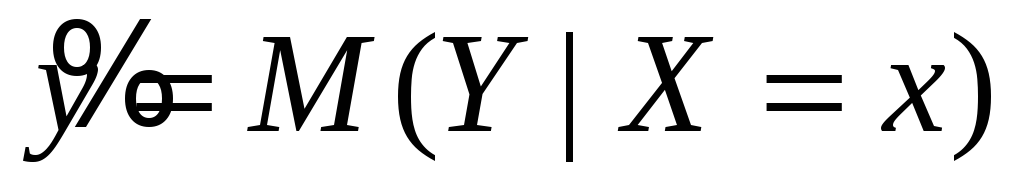при каждом наблюдаемом значении (отобразить графически) (в предположении, что остатки независимые нормальные случайные величины с одинаковой дисперсией).

6. Исследовать подробно свойства остатков, проверить что остатки: а) независимы; б) имеют нормальное распределение; в) гомоскедастичны (имеют одинаковую дисперсию). По результатам исследования сделать выводы о том, какие из ранее полученных оценок нельзя считать достоверными.

Приложение 1. Оценка параметров уравнения линейной регрессии

Рассмотрим линейную по коэффициентам модель регрессии:

, (1)

где - случайная величина с математическим ожиданием равным нулю и дисперсией .

Полагая, перейдем к модели множественной линейной регрессии:

. (2)

Пусть для оценки неизвестных параметров уравнения регрессии (2) взята выборка объемом из значений величин . Тогда

,

где - вектор значений переменной ;

- вектор параметров модели;

– вектор ошибок, где и независимы;

- матрица исходных данных переменных размерами . Первый столбец матрицы содержит единицы (значения фиктивной переменной ), остальные столбцы значения переменных :

.

Для нахождения оценки вектора параметров используем метод наименьших квадратов, согласно которому в качестве оценок берутся такие, которые минимизируют сумму квадратов отклонений значений от :

. (3)

Оценка метода наименьших квадратов имеет вид:

. (4)

Качество регрессионной модели можно оценить, используя оценку дисперсии предсказания :

, где . Также качество модели можно оценить используя оценку коэффициента детерминации: .

Чем ближе значения к 1, тем большую долю дисперсии величины объясняет модель регрессии.

Оценка дисперсии коэффициента находится по формуле: , где соответствующий диагональный элемент матрицы .

Доверительные интервал для находится, используя статистику , которая при нормальном распределении имеет распределение хи-квадрат с степенью свободы.

Для проверки значимости коэффициентов уравнения регрессии используем статистику , которая при истинности гипотезы : , имеет распределение Стьюдента с степенью свободы. Если для заданного уровня значимости значение больше критического , то нулевая гипотеза отвергается и коэффициент признается значимым. В противном случае коэффициент признается незначимым, и соответствующее слагаемое исключается из модели. Доверительные интервалы для коэффициентов находятся используя статистики , имеющие распределение Стьюдента с степенью свободы.

Доверительный интервал для в многомерной точке определяется по формуле: , где квантиль распределение Стьюдента с степенью свободы. Соответственно доверительный интервал для значений в точке будет иметь вид: .

Замечание: Вообще говоря, прежде чем проверять значимость модели, значимость коэффициентов, и строить доверительные интервалы по приведенным выше формулам, следует убедиться в том, что остатки а) независимы; б) имеют нормальное распределение; в) гомоскедастичны (имеют одинаковую дисперсию).

Для проверки независимости остатков временного ряда (или любой другой последовательности случайных величин) можно использовать, например, критерий Спирмена, основанный на статистике, называемой коэффициентом ранговой корелляции Спирмена:

,

где - порядковый номер наблюдения (т.е., в данном случае соответствующего, остатка), - порядковый номер того же наблюдения в вариационном ряду.

Для чисто случайных процессов имеет нулевое математическое ожидание и дисперсию, равную . В больших выборках величина приближенно имеет нормальнее распределение . Для малых выборок предпочтительнее использовать в качестве статистики величину , которая приближенно имеет распределение Стьюдента с степенями свободы. Если искомая расчетная величина по модулю меньше двусторонней критической точки распределения Стьюдента, то нулевая гипотеза о том, что процесс является случайным принимается. И наоборот, если наблюдаемая величина статистики по модулю превосходит табличное значение, то есть значение коэффициента существенно отлично от нуля, то нулевая гипотеза о случайности ряда наблюдений отвергается.

Если наблюдаемая выборка не является последовательностью случайных величин (упорядоченной по времени, либо по какому либо другому фактору), то в этом случае проверка на независимость сводится к проверке независимости остатков от результирующего признака. Для этого можно использовать, например, критерий хи-квадрат Пирсона.

Для проверки нормальности остатков можно использовать критерий хи-квадрат или критерий Харке-Берра, основанный на статистике Харке-Берра: , где - оценки коэффициентов асимметрии и эксцесса. При условии нормальности исходных данных статистика Харке-Берра имеет распределение хи-квадрат с двумя степенями свободы.

Если гипотеза о нормальности остатков принята, то проверку на гомоскедастичность можно провести, например, следующим образом. Разбиваем всю выборку остатков на две последовательные выборки и сравниваем по критерию Фишера выборочные дисперсии обоих выборок. Если они различаются незначимо, то гипотеза о равенстве дисперсий принимается. Данный подход применим для временных рядов и других последовательностей случайных величин. Если наблюдаемая выборка не является последовательностью случайных величин, то ее следует предварительно упорядочить, например, по результирующему признаку, а затем уже разбить на две выборки и применить критерий Фишера. Если гипотеза о нормальности остатков отвергнута, то проверку на гомоскедастичность следует проводить аналогичным образом, но, вместо критерия Фишера, использовать один из непараметрических критериев, например, критерий Клотца.

Приложение 2

Таблица 1.

ВАРИАНТ
1		2		3		4		5
X	Y	X	Y	X	Y	X	Y	X	Y
8,50	17,76	7,82	28,38	9,50	5,14	15,20	28,06	8,58	20,09
3,61	9,47	7,88	36,00	7,77	6,02	12,57	27,42	3,86	17,36
11,22	22,25	10,86	50,64	17,02	25,27	18,36	36,48	6,89	25,53
16,38	27,00	9,96	38,82	4,03	2,74	10,00	23,25	8,17	19,23
15,99	23,06	12,85	67,10	7,35	3,05	17,35	29,80	12,13	22,24
18,67	36,17	9,59	49,28	11,86	9,22	16,99	27,58	10,04	19,29
-0,92	2,49	10,40	53,10	16,34	26,41	11,60	29,25	17,35	27,51
8,83	20,42	9,20	39,09	6,04	-1,02	4,51	14,34	11,06	19,79
15,48	32,47	12,12	64,05	7,11	-6,67	11,85	23,83	16,79	21,71
4,57	2,48	8,97	41,16	7,87	1,77	18,11	32,97	7,68	22,70
6,55	16,25	13,07	61,67	6,21	1,36	16,00	30,76	14,77	25,00
1,55	7,60	12,39	51,49	13,73	15,88	9,91	28,28	12,17	26,34
0,77	9,70	9,76	39,36	3,72	3,06	25,16	35,38	0,13	1,26
5,11	13,19	9,77	36,01	11,83	7,00	17,49	34,53	17,47	28,71
6,13	11,54	7,52	33,42	6,68	7,29	26,61	37,05	6,89	22,39
-0,59	5,72	11,41	52,89	9,35	1,85	12,48	27,16	8,98	21,40
7,16	18,96	1,83	12,69	8,05	5,14	17,01	27,13	17,64	21,65
7,98	12,82	13,42	66,79	11,40	6,88	13,44	32,74	18,94	29,96
10,67	21,25	15,35	82,95	5,37	-3,96	13,62	25,96	6,85	17,97
8,17	18,27	9,93	48,95	14,91	9,45	20,40	35,24	16,60	27,63
8,37	12,39	8,73	23,07	12,05	10,13	12,37	25,66	10,28	20,65
8,15	17,77	10,30	47,83	11,95	10,87	19,70	29,69	0,49	4,82
16,71	30,98	6,46	21,66	11,29	7,86	7,26	21,10	5,86	18,61
9,57	22,84	5,62	16,31	9,56	4,98	13,12	30,52	2,41	17,69
9,07	21,15	13,25	74,47	8,51	2,58	17,15	36,15	2,93	21,61
7,43	14,48	13,63	71,93	6,29	5,55	9,27	23,57	16,35	23,77
19,86	30,30	6,61	18,16	5,17	4,89	9,73	26,00	4,55	19,33
14,33	18,81	9,56	40,17	4,46	4,49	16,30	25,83	4,40	13,83
21,88	41,50	13,52	70,45	11,07	5,47	6,32	17,00	11,99	19,49
6,73	16,72	9,67	40,07	11,80	11,23	18,03	35,51	16,36	29,06
18,31	34,50	10,15	45,16	11,04	6,49	20,63	33,10	6,33	20,56
1,94	9,18	5,52	17,41	7,77	2,68	17,61	27,13	3,68	13,46
12,69	23,46	8,83	38,48	9,98	15,59	13,16	20,68	10,18	15,01
14,51	25,02	12,57	54,62	2,98	6,26	17,84	31,57	4,00	18,19
19,59	28,66	12,94	60,58	10,87	9,43	20,27	38,24	5,68	25,34
9,58	20,53	6,86	30,85	10,58	5,99	17,35	25,76	11,97	18,14
7,38	15,75	11,25	65,14	8,16	6,43	12,53	28,53	6,76	21,30
13,38	25,25	8,23	28,68	7,64	2,54	7,37	21,13	8,38	20,29
8,09	9,75	15,32	82,95	9,93	9,52	14,37	33,50	14,73	28,80
13,79	25,05	12,37	58,89	8,19	6,33	9,69	24,15	4,53	17,50