8. Среднее квадратическое отклонение

Для определения степени колеблемости признаков использует­ся среднее квадратическое отклонение, широко применяемое в эко­номических расчетах.

Среднее квадратическое отклонение бывает простое и взвешенное. Оно обозначается буквой σ.

—простое квадратическое отклонение; —взвешенное квадратическое отклонение.

Рассмотрим порядок вычисления взвешенного среднего квадратического отклонения.

1. Вычисляют СА взвешенную величину из ряда .

1. Определяют отклонения отдельных вариантов от средней.

2. Полученные отклонения возводят в квадрат.

3. Квадраты отклонений делят на увеличивают на число случаев в этих отклонениях, то есть на частоты 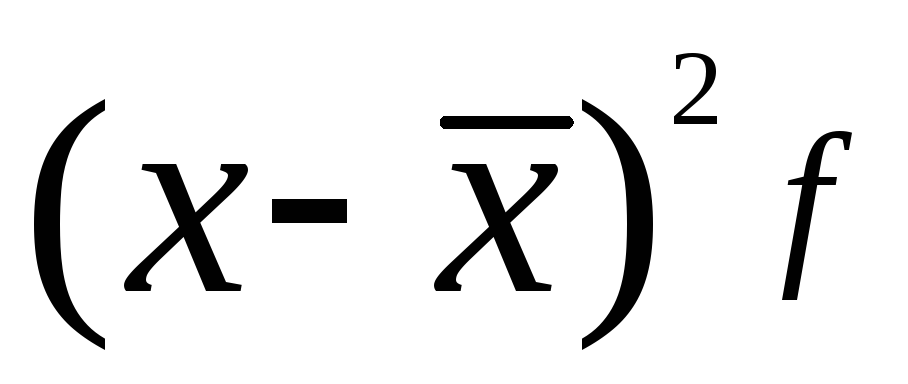. Затем полученные отклонения суммируют.

4. Сумму квадратов отклонений сумму всех чисел членов ряда:

Таким образом, получается дисперсия, или средний квадрат отклонений.

5. Из величины, выражающей дисперсию, извлекают квадратный корень:

Пример. Произведем вычисление простого и взвешенного среднеквадратического отклонения. В табл. 12 показано распреде­ление кип шерсти по массе при отгрузке. Таблица .12

Распределение кип шерсти при отгрузке

Масса одной кипы (), кг	Количество отгруженных кип (f), шт
86	10
90	20
94	10
96	30
100	15
110	15
ИТОГО	100

Требуется определить СА простую и взвешенную, среднее квадратическое отклонение простое и взвешенное.

1. Определяем средний вес одной кипы, для чего используем формулу средней арифметической простой:

Подставим значения:

2. Среднее квадратическое простое отклонение (не взвешенное) определяем по формуле:

Для расчета квадратического отклонения построим расчетную таблицу(таб. .13). Таблица .13

Данные для расчета квадратического отклонения

Масса кипы шерсти, кг	Отклонение от средней (= 96 кг)	Квадраты отклонений (х-ха)2
86	-10(86-96)	100
90	-6	36
94	-2	4
96	0	0
100	+4	16
110	+14	196
ИТОГО

Что характеризует полученное квадратическое отклонение?

Масса отдельных кип шерсти отклоняется от средней (96 кг) в одних случаях на большую величину, в других— на меньшую. В среднем это отклонение от средней составляет ±7,7 кг. Из этих данных видно и другое: простое среднее квадратическое отклонение выражается в тех же именованных числах, что и средняя величина. Поэтому оно составляет так называемое абсолютное отклонение от средней величины. По данным примера рассчитаем также среднее квадратическое отклонение (взвешенное) для характеристики ряда распределения с неравными частотами. Для этого примем во внимание количество отгруженных кип, которые будут составлять частоты(f).

Расчет производим по формуле:

Построим расчетную таблицу (табл. .14).

Сначала определяем среднюю арифметическую взвешенную:

Рассчитаем среднее квадратическое отклонение (взвешенное):