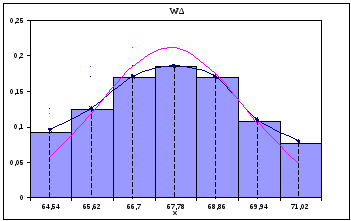
4) Сравнение эмпирического и теоретического законов распределения случайной величины X.

Из вида кривой эмпирического распределения следует, что случайная величина должна иметь закон распределения, близкий к нормальному. Для сравнения в той же системе координат построим кривую нормального закона распределения

,

где , а величиныибыли получены в предыдущем пункте. Таким образом,.

Одним из критериев, позволяющих установить справедливость нормального закона распределения случайной величины X, является правило трех сигм. В случае нормально распределенной величины вероятность отклонений от больше, чем на величину, мала, следовательно такие отклонения встречаются крайне редко. Для наших статистических данных. Из графика и таблицы можно сделать вывод, что величинаX редко отклоняется от более, чем на, следовательно, ее закон распределения близок к нормальному.

Приложения

ОГЛАВЛЕНИЕ

Таблицы вариантов………………………………………………………………	2
Задания для контрольных работ. Контрольная работа №1…………………...	4
Контрольная работа №2…………………………………………………………	9
Решение типовых примеров. Контрольная работа №1….…………………….	21
Решение типовых примеров. Контрольная работа №2….…………………….	33
Приложения………………………………………………………………………	53

55