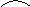- •Высшая математика
- •Предисловие
- •Таблицы вариантов
- •Специальность мсх
- •Специальность эасх
- •Специальность эасх
- •Задания для контрольных работ
- •Решение типовых примеров контрольная работа №1
- •Контрольная работа №2
- •Решение. 1) Построение статистического распределения выборки.
- •2) Оценка среднего значения и дисперсии случайной величины .
- •3) Построение гистограммы относительных частот.
- •4) Сравнение эмпирического и теоретического законов распределения случайной величины X.
- •Приложения
Решение типовых примеров контрольная работа №1
1. Привести уравнения данных гармонических колебаний
![]()
к виду ![]() .
.
Найти амплитуду
А,
фазу
![]() ,
период гармоники и построить ее график.
,
период гармоники и построить ее график.
Решение. Привести уравнения данных гармонических колебаний
![]()
к виду ![]() ,
где
,
где![]() – амплитуда,
– амплитуда,![]()
![]() ,
,![]() и
и![]() – период колебания.
– период колебания.
В нашем случае:
![]() ,
,
![]() и
и![]() ,
,![]() ,
откуда
,
откуда![]() принадлежит 4 четверти и
принадлежит 4 четверти и![]() ,
,![]() .
Тогда
.
Тогда
![]() ,
,![]() .
.
От графика функции
![]() перейдем к графику функции
перейдем к графику функции![]() с помощью следующей цепочки преобразований:
с помощью следующей цепочки преобразований:
![]()
то есть нашу функцию
![]() .
.
Построение:
Стоим одну волну синусоиды
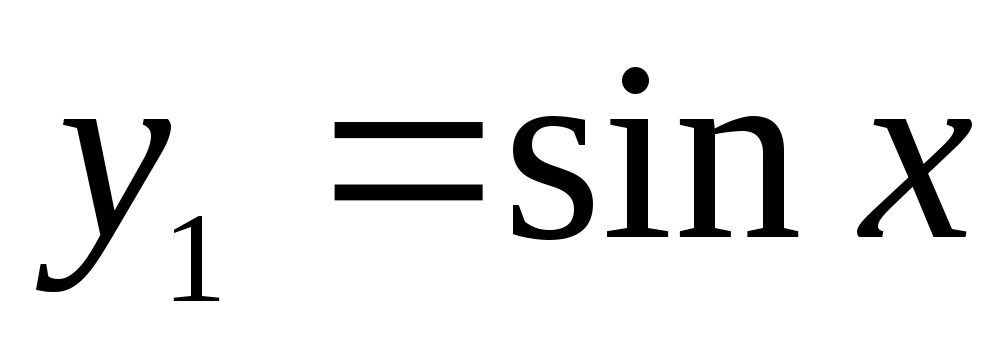 .
.Строим график функции
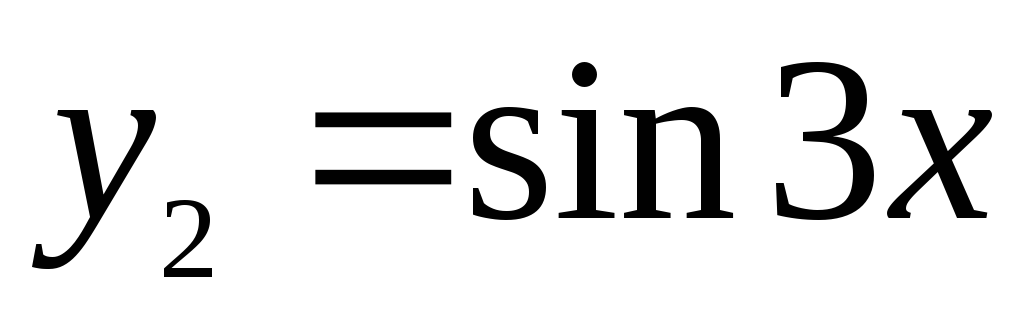 ,
которая имеет период
,
которая имеет период
 (то есть сжимаем функцию
(то есть сжимаем функцию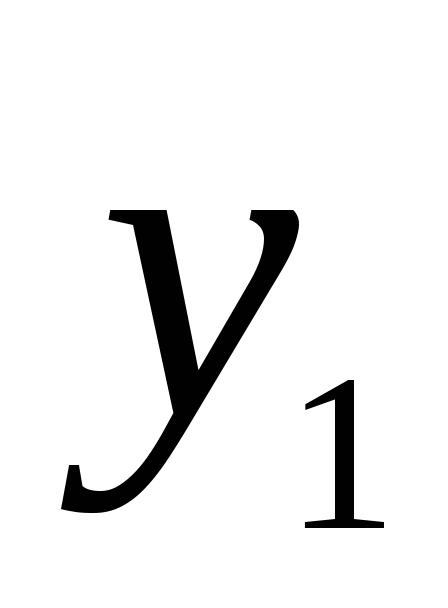 в три раза).
в три раза).У

 величивая
ординаты графика
величивая
ординаты графика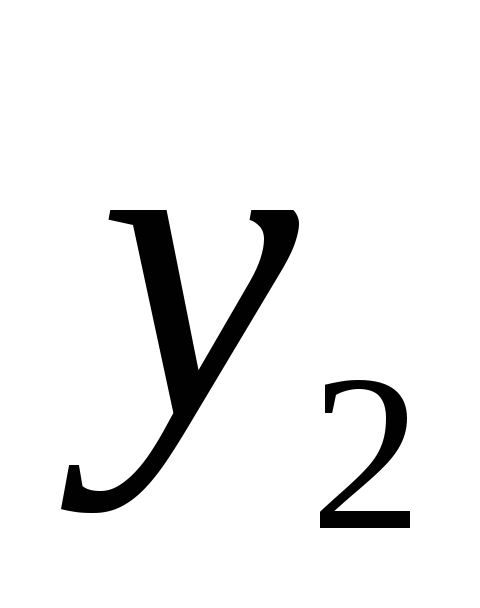 в 5 раз, получаем график функции
в 5 раз, получаем график функции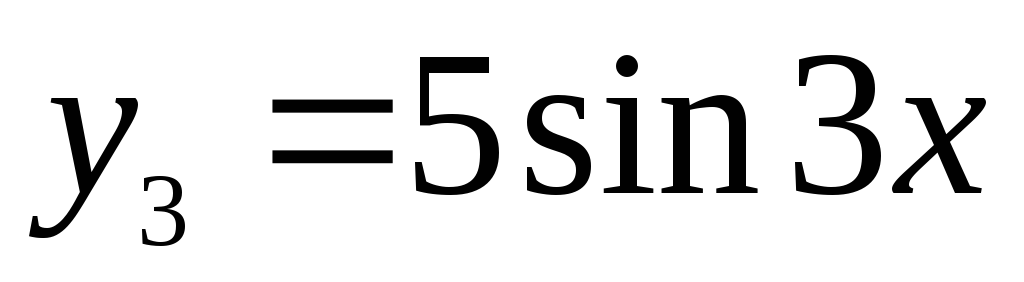 .
.Сдвигаем график функции
 на 12,30
вправо вдоль оси Ох.
на 12,30
вправо вдоль оси Ох.
 у
у


 5
5


 1
1



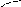
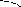 1200132,30
1200132,30
0 12,3060018003600х
у2=sin3xу1=sinx
у3=5sin3x у=5sin(x–12,30)
2. Решить систему линейных уравнений методом Крамера.
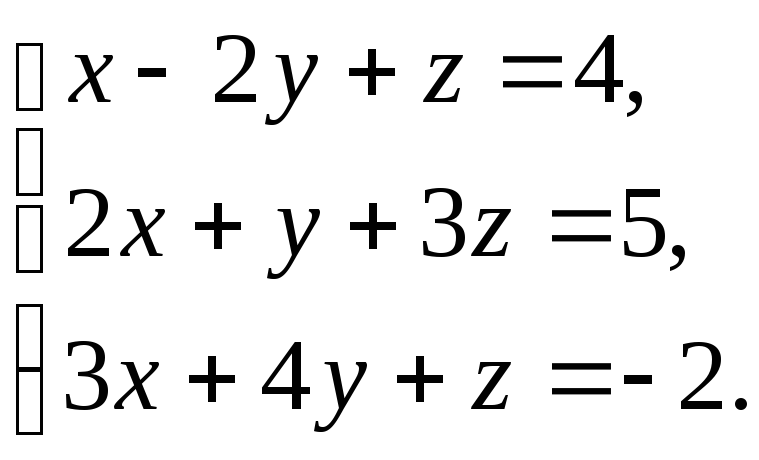
Решение. Подсчитаем
сначала главный определитель системы
![]() ,
воспользовавшись следующим правилом
вычисления определителей третьего
порядка:
,
воспользовавшись следующим правилом
вычисления определителей третьего
порядка:
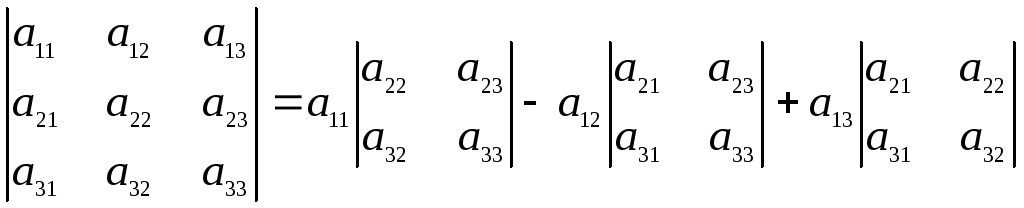 .
.
У нас
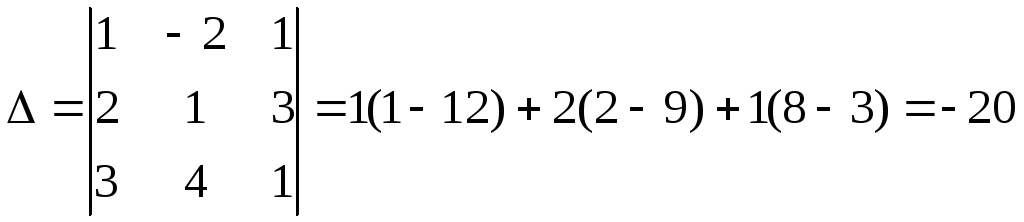 .
.
Так как
![]() ,
система имеет единственное решение.
Вычислим вспомогательные определители
,
система имеет единственное решение.
Вычислим вспомогательные определители![]() .
.
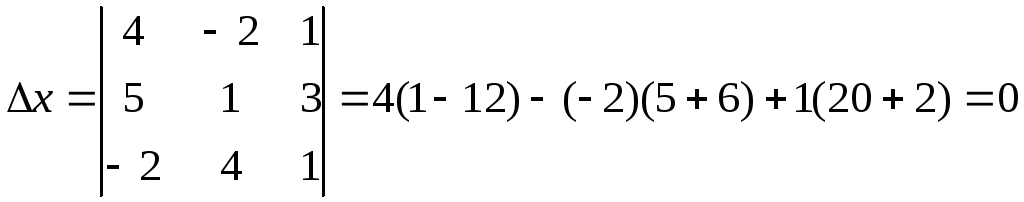 ;
;
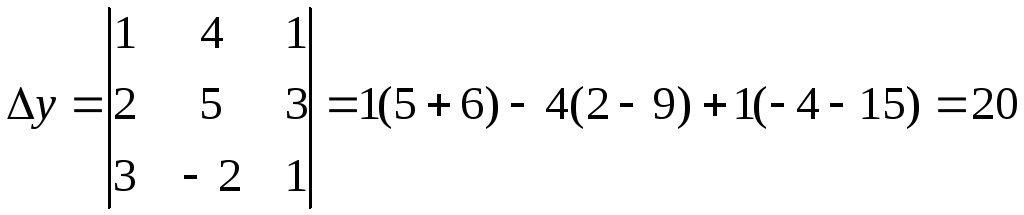 ;
;
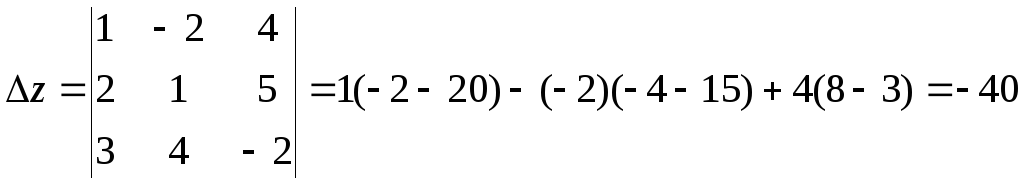 .
.
Воспользовавшись формулами Крамера, получим
![]()
Проверим правильность полученного решения, подставив его в каждое уравнение заданной системы:
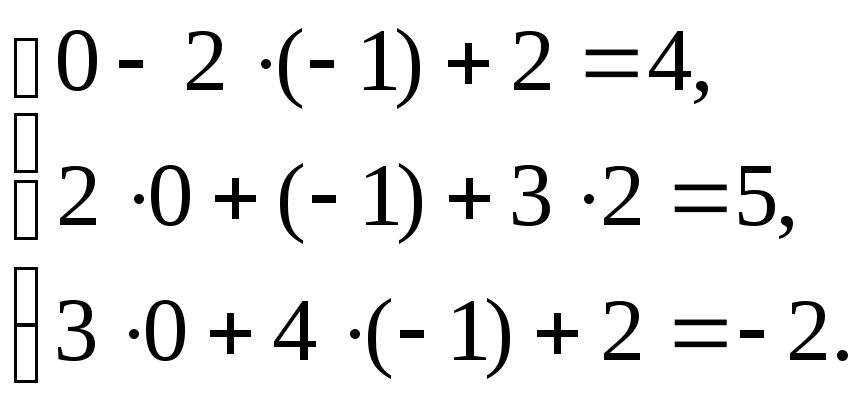
3.
Определить тип кривой
![]() ,
найти ее параметры; определить угловой
коэффициент прямой
,
найти ее параметры; определить угловой
коэффициент прямой
![]() .
Найти точки пересечения данных линий
и сделать чертеж.
.
Найти точки пересечения данных линий
и сделать чертеж.
Решение. Приведем
уравнение кривой
![]() к каноническому
виду
к каноническому
виду
![]() ,
разделив на 225. Получим уравнение эллипса
,
разделив на 225. Получим уравнение эллипса
![]() .Его большая
полуось
.Его большая
полуось
![]() ,
малая полуось
,
малая полуось![]() .
Центр совпадает с началом координат.
.
Центр совпадает с началом координат.
Уравнение прямой
![]() имеет вид «в отрезках»
имеет вид «в отрезках»![]() ,
что удобно для построения. Для нахождения
углового коэффициента прямой приведем
ее к виду
,
что удобно для построения. Для нахождения
углового коэффициента прямой приведем
ее к виду![]() ,
выразиму
через х:
,
выразиму
через х:
![]() .
.
Угловой коэффициент
![]() .
.
Для нахождения точек пересечения этих линий решим систему
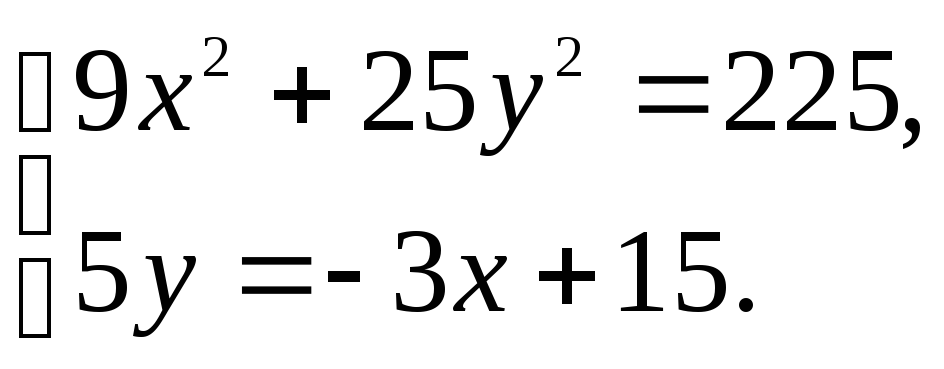
Возведем второе уравнение в квадрат
![]()
и подставим в первое уравнение:
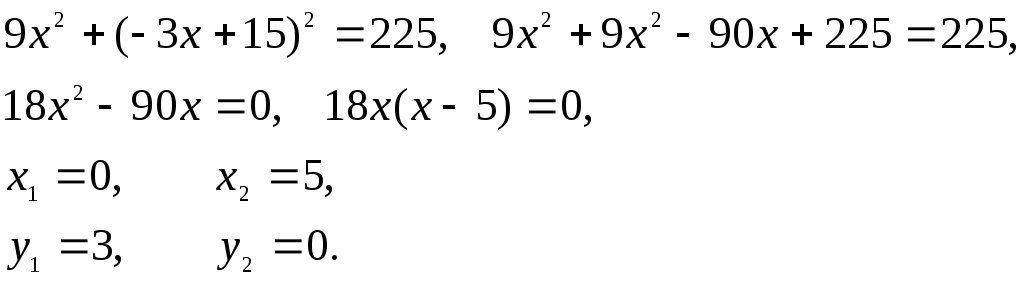
Нашли точки пересечения (0; 3) и (5; 0), что наглядно видно на чертеже.

 у
у
3


–5 0 5 х
–3
4.
Даны координаты вершин пирамиды АВСD:
![]()
![]() Требуется:
Требуется:
1) записать векторы
![]() в системе орт
в системе орт![]() и найти модули этих векторов;
и найти модули этих векторов;
2) найти угол между
векторами
![]() и
и
![]() ;
;
3) найти проекцию
вектора ![]() на вектор
на вектор ![]() ;
;
4) найти площадь грани АВС;
5) найти объем пирамиды АВСD;
6) составить уравнение ребра АС;
7) составить уравнение грани АВС.
Решение.
1) Произвольный
вектор
![]() представляется в системе орт
представляется в системе орт![]() по формуле
по формуле
![]() ,
,
где
![]() – координаты вектора
– координаты вектора![]() .
Если заданы точки
.
Если заданы точки![]() ,
,![]() ,
то для вектора
,
то для вектора![]()
![]() ,
,
то есть
![]() .
.
Воспользовавшись формулой и координатами заданных точек А, В, С, D, получим:
![]() ;
;
![]() ;
;
![]() .
.
Если вектор
![]() ,
то его модуль вычисляется по формуле:
,
то его модуль вычисляется по формуле:
![]() .
.
Модули найденных векторов
![]() ;
;
![]() ;
;
![]() .
.
2) Известна формула
![]() ,
,
где ![]() – скалярное произведение векторов
– скалярное произведение векторов
![]() и
и![]() ,
которое можно вычислить следующим
образом:
,
которое можно вычислить следующим
образом:
![]() .
.
У нас
![]() ,
,
то есть
![]() .
.
3) Известно, что
![]() ,
,
то есть в нашем случае
![]() .
.
4) Воспользуемся
формулой нахождения площади треугольника,
построенного на векторах
![]() и
и![]()
![]() ,
,
где ![]() – векторное произведение векторов,
которое можно вычислить по следующему
правилу:
– векторное произведение векторов,
которое можно вычислить по следующему
правилу:
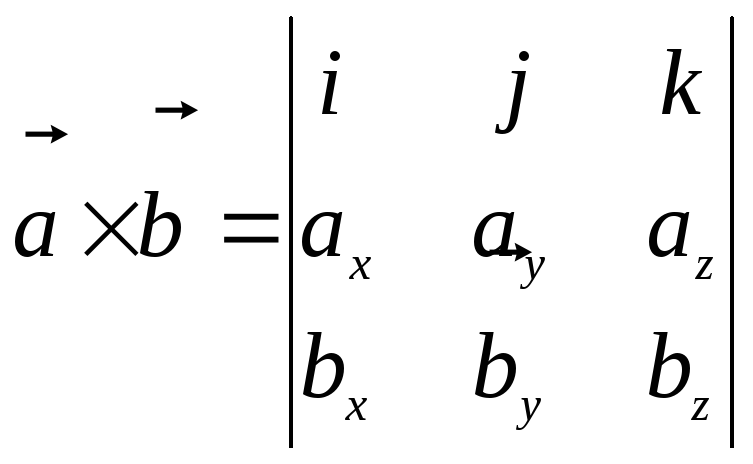 .
.
В нашем примере
![]() ,
причем
,
причем
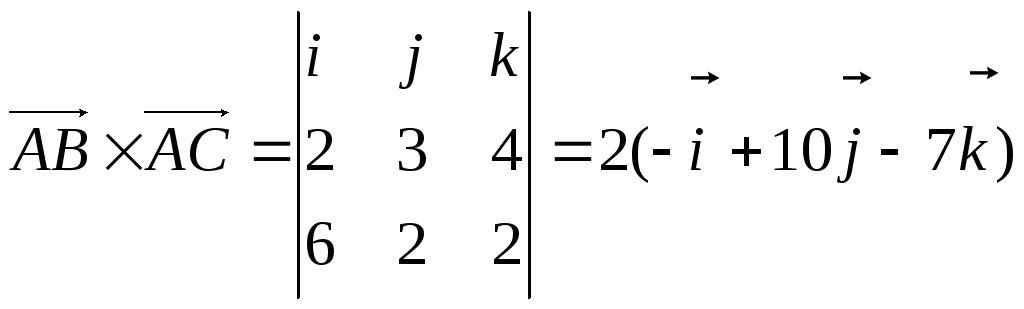 .
.
Таким образом,
![]() (кв. ед.).
(кв. ед.).
5) Объем пирамиды,
построенной на трех некомпланарных
векторах
![]() можно найти по формуле
можно найти по формуле
![]() ,
,
где ![]() – смешанное произведение векторов,
которое вычисляется следующим образом:
– смешанное произведение векторов,
которое вычисляется следующим образом:
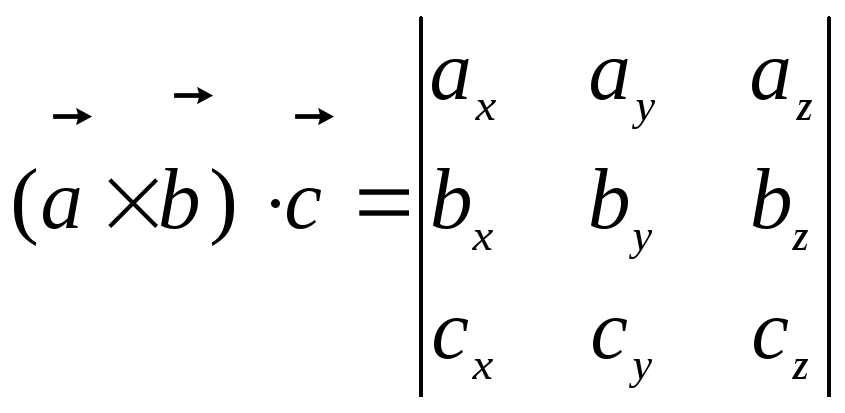 .
.
У нас
![]() ,
где
,
где
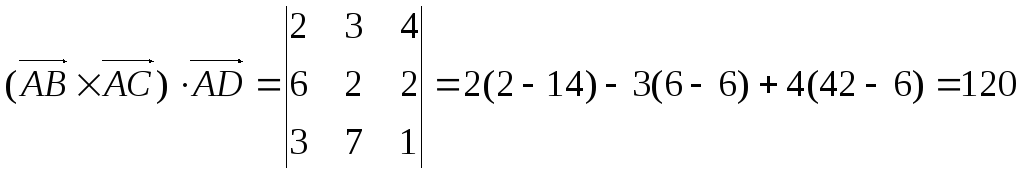 ,
,
то есть
![]() (куб. ед.).
(куб. ед.).
6) Известно, что
уравнение прямой, проходящей через две
заданные точки
![]() и
и![]() имеет вид:
имеет вид:
![]() .
.
Подставив координаты точек А и С, получим
![]() ,
,
то есть уравнение ребра АС окончательно запишется следующим образом:
![]() или
или![]() .
.
7) Уравнение
плоскости, проходящей через три заданные
точки
![]() ,
,![]() ,
,![]() можно записать в виде
можно записать в виде
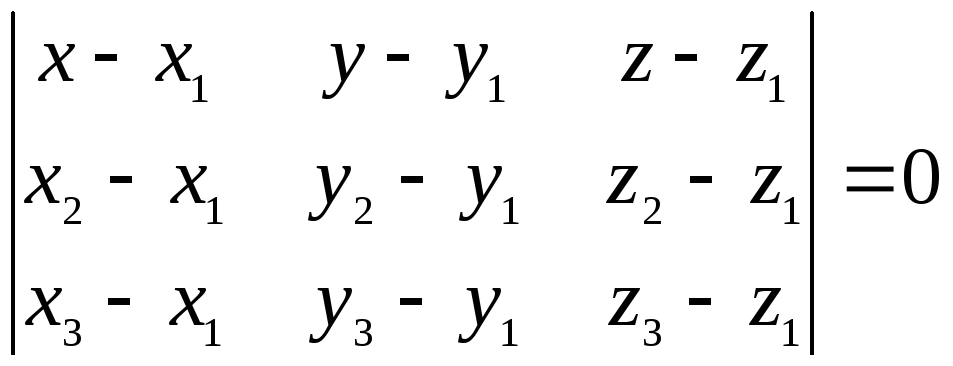 .
.
Подставляя в него координаты точек А, В, С, получим
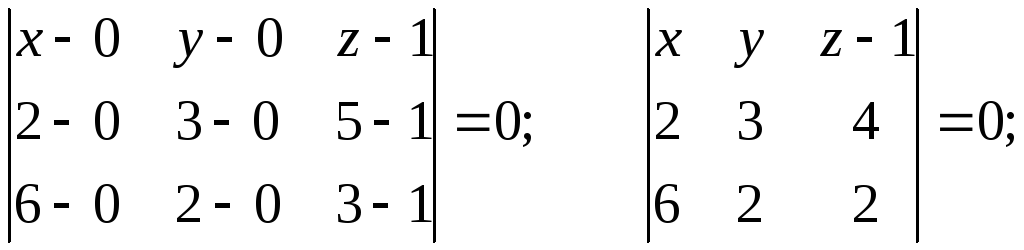
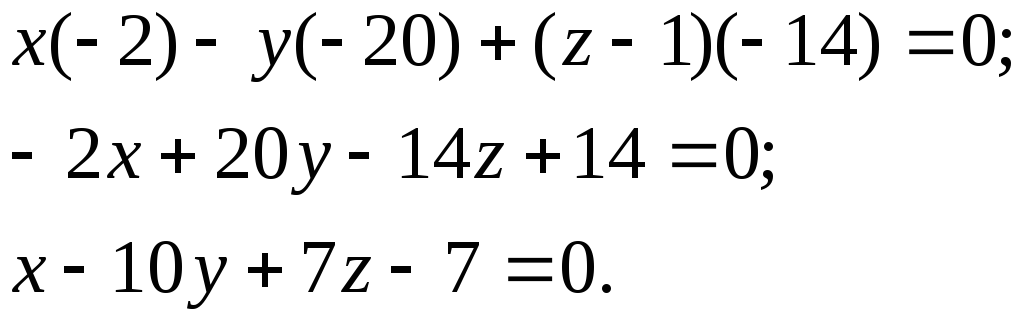
5. Провести
полное исследование функции
![]() методами
дифференциального исчисления и построить
ее график.
методами
дифференциального исчисления и построить
ее график.
Решение.
1) Область определения функции
![]() .
.
2) Исследование на непрерывность и классификация точек разрыва.
Заданная функция непрерывна всюду, кроме точки х = 4. Вычислим ее односторонние пределы в этой точке:
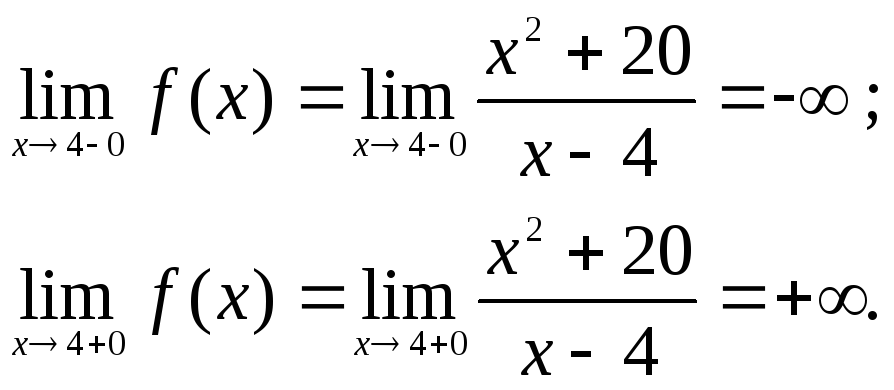
Таким образом, точка х = 4 является для заданной функции точкой разрыва второго рода, а прямая х = 4 – вертикальной асимптотой графика.
3) Исследование на экстремум и промежутки монотонности.
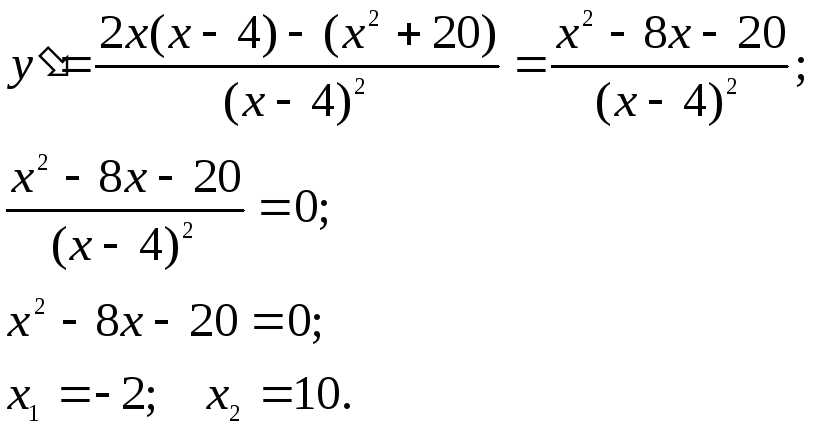
|
х |
|
–2 |
(–2; 4) |
4 |
(4; 10) |
10 |
|
|
|
+ |
+ |
– |
не сущ. |
– |
0 |
+ |
|
|
|
max |
|
|
|
min |
|
![]() .
.
4) Исследование графика на выпуклость, вогнутость, точки перегиба.
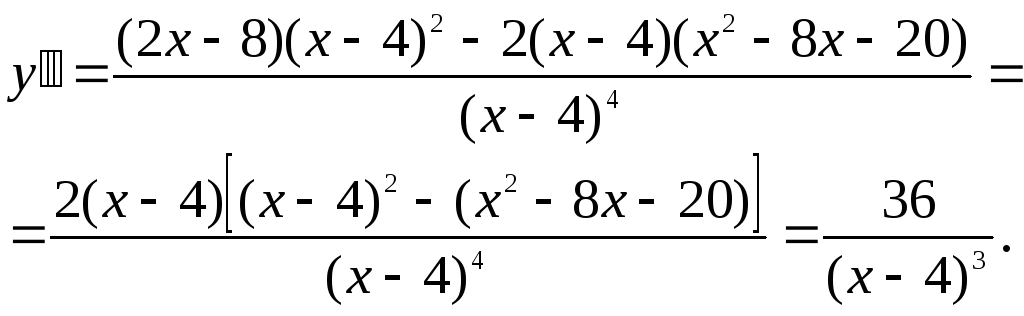
Так как
![]() ,
то график заданной функции точек перегиба
не имеет. Остается выяснить вопрос об
интервалах его выпуклости и вогнутости:
,
то график заданной функции точек перегиба
не имеет. Остается выяснить вопрос об
интервалах его выпуклости и вогнутости:
|
х |
|
4 |
|
|
|
– |
не сущ. |
+ |
|
|
|
|
|
5) Исследование графика на наличие наклонных асимптот.

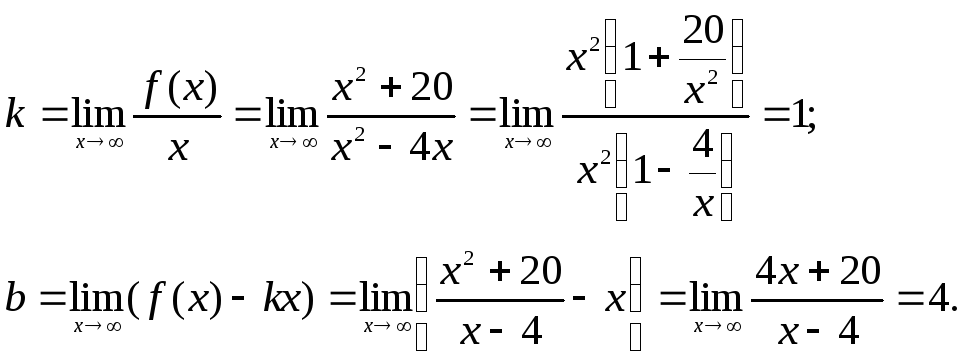
Таким образом,
прямая
![]() – наклонная асимптота графика.
– наклонная асимптота графика.
6) График заданной функции пересекает ось Оу в точке (0; –5).
По результатам исследования строим график.

 у
у
20
4

–4 0 4 х

6.
Решить систему двух линейных уравнений
в области комплексных чисел по формулам
Крамера. Найденные
![]() изобразить
на комплексной плоскости;
изобразить
на комплексной плоскости;![]() ,
,
![]() записать в показательной и тригонометрической
формах.
записать в показательной и тригонометрической
формах.
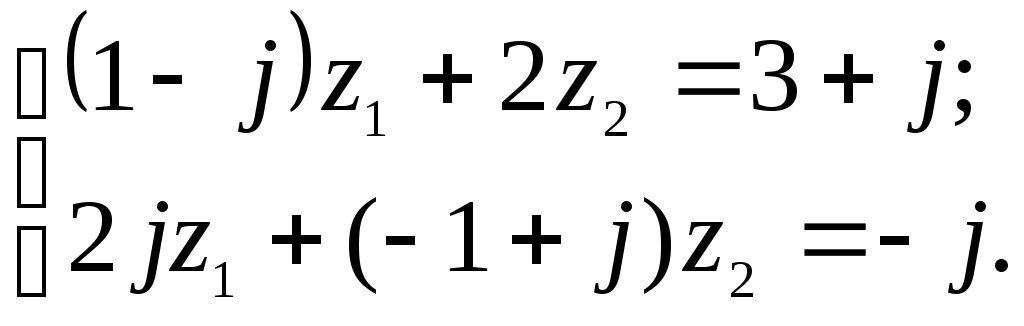
Решение. Найдем
решение системы линейных уравнений по
формулам Крамера
![]() .
Для этого вычислим главный определитель
системы
.
Для этого вычислим главный определитель
системы![]() и определители
и определители![]() ,
учитывая, что
,
учитывая, что![]() – комплексное число, где
– комплексное число, где![]() .
.
![]()
![]()
![]()
Находим ![]() :
:
![]() (т.к.
(т.к.![]() );
);
![]()
Таким образом, решение данной системы уравнений в алгебраической форме записи:
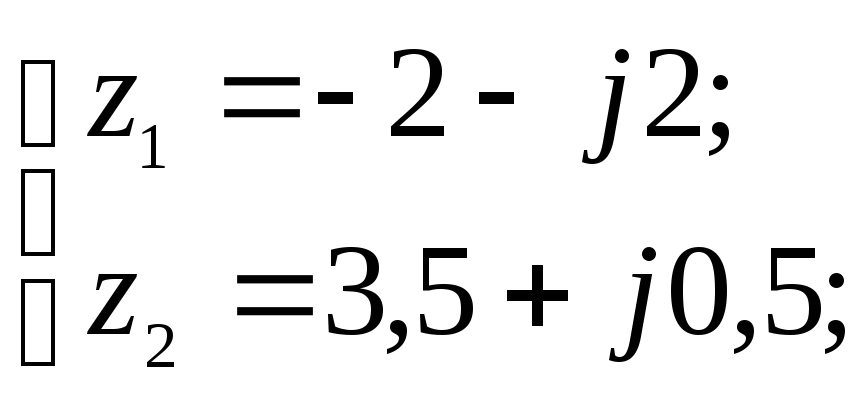
в векторной форме записи
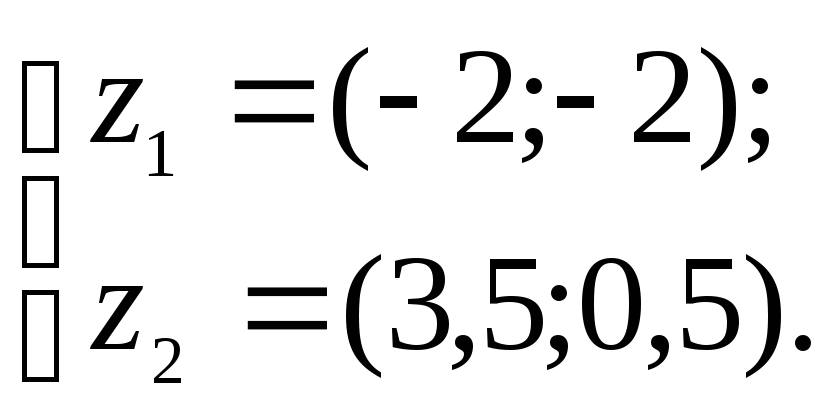
Для того, чтобы
найти
![]() в алгебраической форме, складываем
действительные и мнимые части чисел
в алгебраической форме, складываем
действительные и мнимые части чисел![]() :
:
![]() .
.
Вектор, соответствующий
числу
![]() ,
строим как сумму векторов по правилу
параллелограмма.
,
строим как сумму векторов по правилу
параллелограмма.
Для того, чтобы
найти
![]() в алгебраической форме, вычитаем
действительные и мнимые части чисел
в алгебраической форме, вычитаем
действительные и мнимые части чисел![]() :
:
![]() .
.
Вектор, соответствующий
числу
![]() ,
записываем как сумму векторов
,
записываем как сумму векторов![]() и
и![]() , строим его по правилу параллелограмма.
, строим его по правилу параллелограмма.
 у
у
–3,5 z2






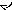
– z2–2 0 3,5 x
 z1z
z1z
 и
и
Найдем модуль
![]() и аргумент
и аргумент![]() комплексных чисел
комплексных чисел![]() (
(![]() или
или
![]() ;
;![]() в
1 и 4 четвертях;
в
1 и 4 четвертях;![]() во 2 и 3 четвертях, знак «+» или «–»
выбираем так, чтобы аргумент был
наименьшим по модулю).
во 2 и 3 четвертях, знак «+» или «–»
выбираем так, чтобы аргумент был
наименьшим по модулю).
Число ![]() принадлежит 3
четверти:
принадлежит 3
четверти:
![]() (аргумент
(аргумент
![]() );
);
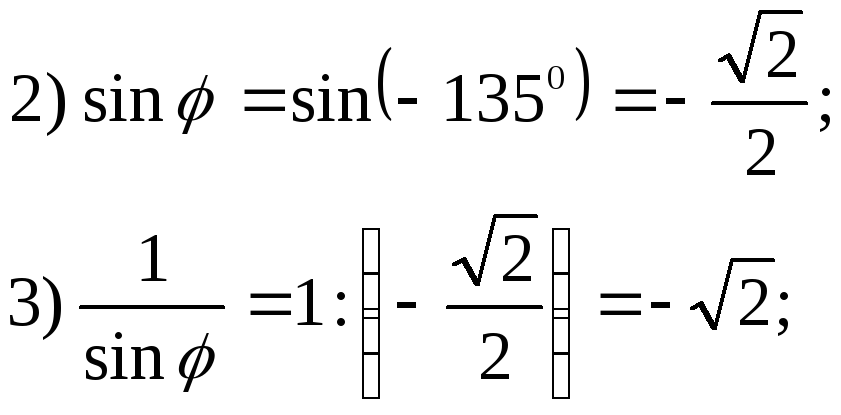
![]() (модуль
(модуль
![]() ).
).
Число ![]() принадлежит 1
четверти:
принадлежит 1
четверти:
![]() ;
;
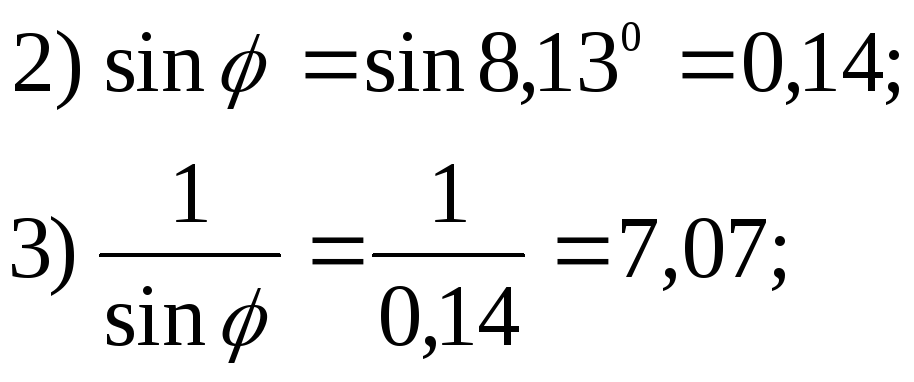
![]()
Запишем числа
![]() в показательной
в показательной![]() и тригонометрической
и тригонометрической![]() формах:
формах:
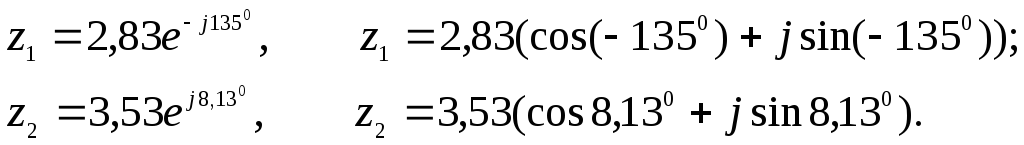
![]()
так как при умножении комплексных чисел их модули перемножаются, а аргументы складываются.
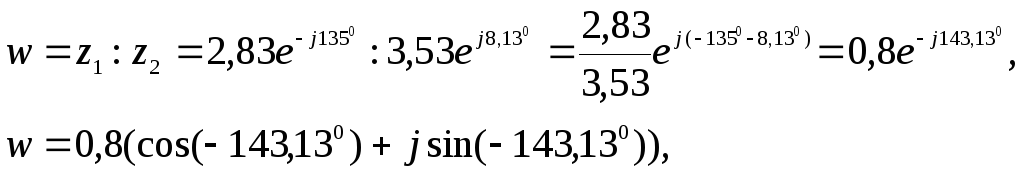
так как при делении комплексных чисел их модули делятся, а аргументы вычитаются.
7. а) Вычислить
площадь фигуры, ограниченной заданными
параболами
![]() .
.
б)
Найти объем тела, образованного
вращением вокруг оси Ох
фигуры,
расположенной в первом квадранте и
ограниченной заданными параболой ![]() ,
прямой
,
прямой
![]() и осью Ох.
и осью Ох.
Решение.
а) Найдем абсциссы точек пересечения заданных парабол. Для этого приравняем правые части их уравнений:
![]() .
.
Отсюда
![]()
![]() .
.
у

 1
1

–1 0 1 х

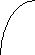



Площадь вычислим по формуле
![]() ,
,
где ![]() ,
,
![]() – кривые, ограничивающие фигуру (
– кривые, ограничивающие фигуру (![]() ).
).
В нашем случае
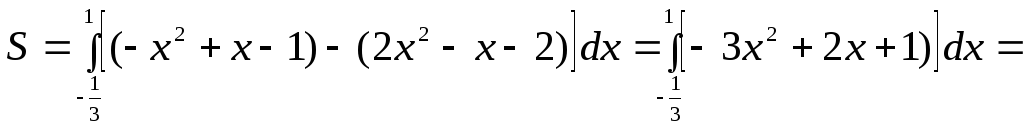
![]()
б) Найдем абсциссу точки пересечения параболы и прямой в первом квадранте. Для этого решим уравнение
![]() ,
,
![]() ,
,
![]() .
.
Первому квадранту
соответствует корень ![]() .
.
Найдем теперь
абсциссу точки пересечения прямой с
осью Ох,
решив уравнение
![]() ,
откуда
,
откуда![]() .
.
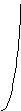
 Таким
образом, можно считать, что тело вращения
ограничено при
Таким
образом, можно считать, что тело вращения
ограничено при![]() поверхностью, образованной вращением
параболы
поверхностью, образованной вращением
параболы![]() вокруг осиОх,
а при
вокруг осиОх,
а при
![]() – вращением прямой
– вращением прямой![]() .
.
 у
у
8





0 2 х
Объем ищем по формуле
![]() .
.
 .
.
Для вычисления
второго интеграла используем подстановку
![]() .
Тогда
.
Тогда![]() и
и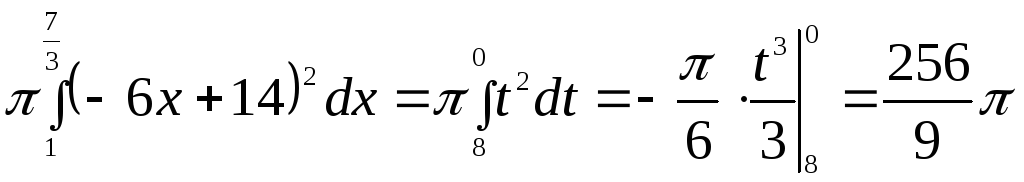 .
.
Отсюда
![]() .
.