Данные расчета приведены в таблице 6

Таблица 6

t	таб)	факт)
0	1,927	0,714
3	1,704	0,631
6	1,524	0,564
9	1,378	0,510
12	1,259	0,466
15	1,161	0,430
18	1,080	0,400
21	1,012	0,375
24	0,956	0,354
27	0,908	0,336
30	0,867	0,321

Продолжение таблицы 6

33	0,832	0,308
36	0,801	0,297
39	0,774	0,287
42	0,750	0,278
45	0,728	0,270
48	0,708	0,262
51	0,689	0,255
54	0,672	0,249
57	0,656	0,243
60	0,641	0,237
63	0,627	0,232
66	0,613	0,227
69	0,600	0,222
72	0,587	0,217
75	0,575	0,213
78	0,563	0,209
81	0,552	0,204
84	0,541	0,200
87	0,530	0,196
90	0,520	0,193
93	0,509	0,189
96	0,499	0,185
99	0,489	0,181
102	0,480	0,178
105	0,470	0,174
108	0,461	0,171
111	0,452	0,167
114	0,443	0,164
117	0,435	0,161
120	0,426	0,158

По данным таблицы 6 строится график (рис 3.)

Сравнивая графики суммарной девиации гирокомпаса “Курс – 4” для стандартного маневра и данного варианта определяем, что величина δj(таб.)> δj(факт.)

Задание 2.3

Произвести оценку максимально возможного значения результирующей инерционной девиации δj(мах), которая возникает в показаниях гирокомпаса в следствии её накопления при выполнении судном повторных манёвров, а также определить интервал времени между манёврами, при котором происходит максимально возможное накопление. Управление судном происходит по гирокомпасу “Курс-4”.

Управление судном происходит по гирокомпасу “Курс-4”.В силу сложившейся обстановки возникла необходимость двигаться переменными курсами и сделать последовательно несколько поворотов. Характеристики маневрирования определяются из таблицы (7).

Таблица 7

Широта места, φ	КК1	КК2	КК3	КК4	V1=V2=V3=V4, узлы
75	10	172	15	160	15

Предполагаем, что повороты делались достаточно быстро. При быстром манёвре оценивать его влияние на гирокомпас можно с помощью величины  VN

 VN =V2*cosKK2 – V1 * cosKK1

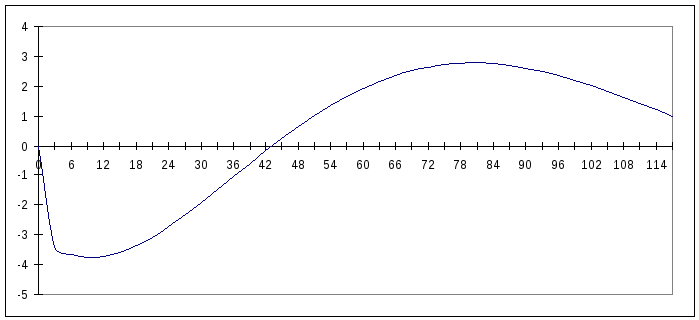
То есть, для оценки величины суммарной инерционной девиации при произвольном манёвре судна допустимо использовать её значение при равноускоренном движении судна в соответствующей широте места и длительностью манёвра t=1 мин. Используя таблицу (8) строим график суммарной инерционной девиации гирокомпаса “Курс-4” для стандартного манёвра на курсе 180⁰ (рис 4.), набор скорости от 0 до 25 узлов, т.е. для VN=25 узлов, широте места φ=75⁰ и времени t1=1мин.

Таблица 8

t				
0	0	0,000	0,000	0,000
3	-3,4	-2,073	2,053	-2,000
6	-3,66	-2,231	2,210	-2,153
9	-3,76	-2,292	2,270	-2,212
12	-3,73	-2,274	2,252	-2,194
15	-3,59	-2,189	2,168	-2,112
18	-3,37	-2,054	2,035	-1,982
21	-3,08	-1,878	1,860	-1,812
24	-2,73	-1,664	1,648	-1,606
27	-2,34	-1,427	1,413	-1,376
30	-1,92	-1,171	1,159	-1,129
33	-1,49	-0,908	0,900	-0,876

Продолжение таблицы 8

36	-1,05	-0,640	0,634	-0,618
39	-0,61	-0,372	0,368	-0,359
42	-0,18	0,146	-0,145	0,141
45	0,24	0,390	-0,386	0,376
48	0,64	0,616	-0,610	0,594
51	1,01	0,823	-0,815	0,794
54	1,35	1,012	-1,002	0,976
57	1,66	1,177	-1,165	1,135
60	1,93	1,323	-1,310	1,276
63	2,17	1,439	-1,425	1,388
66	2,36	1,536	-1,522	1,482
69	2,52	1,609	-1,594	1,553
72	2,64	1,658	-1,642	1,600
75	2,72	1,689	-1,673	1,629
78	2,77	1,695	-1,679	1,635
81	2,78	1,677	-1,660	1,618
84	2,75	1,646	-1,630	1,588
87	2,7	1,591	-1,576	1,535
90	2,61	1,524	-1,510	1,471
93	2,5	1,439	-1,425	1,388
96	2,36	1,341	-1,328	1,294
99	2,2	1,238	-1,226	1,194
102	2,03	1,122	-1,111	1,082
105	1,84	0,994	-0,984	0,959
108	1,63	0,866	-0,857	0,835
111	1,42	0,738	-0,731	0,712
114	1,21	0,604	-0,598	0,582
117	0,99	0,000	0,000	0,000

Перестраиваем стандартный график девиации на три новые графика. Для этого используем следующие формулы:

δj(факт)= - δj(таб)*ΔVN j (факт)

25

где ΔVN j (факт)=Vj+1*cos KK j+1 – V1 cos KK j ( j =1,2,3)

Данные расчетов для новых графиков приведены в таблице (8) в интервале от t=0 до t=117мин.

По данным таблицы (8) строим графики девиации и совмещаем их в общее начало координат (рис 5.). Далее раздвигая второй и третий графики по времени, определяем интервал времени между маневрами, при которых произойдет максимальное по величине накопление результирующей девиации. Далее строим график результирующей девиации (Рис 6.).

При маневрировании судна в показаниях гирокомпаса в общем случае возникают одновременно инерционные девиации первого и второго рода. Судоводителю приходится иметь дело с суммарной инерционной девиацией, которая может накапливаться при повторном маневрировании. В нашем случае, в момент времени t=81 мин., при повторном маневре, инерционная девиация (результирующая) достигает величины δ=2,78 , а в момент времени t =9 мин, при выполнении третьего маневра, результирующая инерционная девиация достигает δ= - 3.76 , что крайне отрицательно влияет на точность судовождения. В этом случае судоводителю следует считаться с тем, что в течение нескольких часов показания гирокомпаса будут неточны. Необходимо стремиться к тому, чтобы маневры делались быстро и последующие маневры выполнялись через равные промежутки времени.

Из графика результирующей девиации (рис 6.) выбираем два пиковых значения девиации δмах=3,76 и δмин= - 2,78.