Лекция 9

Равновесие плазмы в термоядерных установках. Импульсные системы. Z-пинчи.

Проблемы равновесия плазменных конфигураций, МГД-устойчивость плазмы, лежащей на магнитном поле, устойчивость скинированного пинча.

Важный круг задач, в которых с успехом применяется магнитная гидродинамика, связан со стационарными течениями плазмы, т.е. с такими, когда параметры течения явно не зависят от времени и частные производные по времени в уравнениях (3.4)  (3.10) можно опустить. Частным случаем стационарных процессов являются статические равновесия, когда скорость плазмы тождественно равна нулю. Это именно равновесия, так как из условия вытекает , а, следовательно, действующие на любой элементарный объем плазмы силы должны быть уравновешены. При этом, как это видно из уравнения движения (8.5), должно быть выполнено условие:

. (9.1)

Это условие и представляет собой уравнение равновесия плазмы в магнитной гидродинамике. Из него, очевидно, следует, что вектора и лежат на поверхностях, ортогональных к градиенту давления, то есть на поверхностях постоянного давления p=const. С другой стороны, если магнитной конфигурации сопоставить семейство магнитных поверхностей, на которых лежат силовые линии, то, очевидно, что именно на этих поверхностях давление плазмы должно быть постоянно. Таким образом, магнитные поверхности удерживающего плазму магнитного поля с необходимостью должны быть изобарическими для плазмы.

В простейшем случае, когда силовые линии магнитного поля являются прямолинейными и параллельными друг другу, их радиус кривизны равен бесконечности, то согласно выражению (8.16) можно записать

. (9.2)

Выбрав направление силовых линий за ось z системы координат, для единственной отличной от нуля компоненты поля B_z из уравнения соленоидальности магнитного поля

получим

,

и магнитная индукция может меняться только поперек направления силовых линий. Воспользовавшись представлением (9.2) для силы Ампера, из уравнения (9.1) получим

, ,

следовательно, давление плазмы также не меняется вдоль силовых линий, а поперек силовых линий должна быть постоянна сумма давления плазмы и магнитного давления:

.

Согласно этому условию вне области, занятой плазмой, магнитное поле является однородным, пусть здесь B_z=B₀. Тогда постоянную можно выбрать так, что во всем пространстве будет

. (9.3)

Видно, что в области, занятой плазмой, магнитное поле меньше внешнего. Можно сказать, что плазма «выталкивает» магнитное поле, как и любой другой диамагнетик.

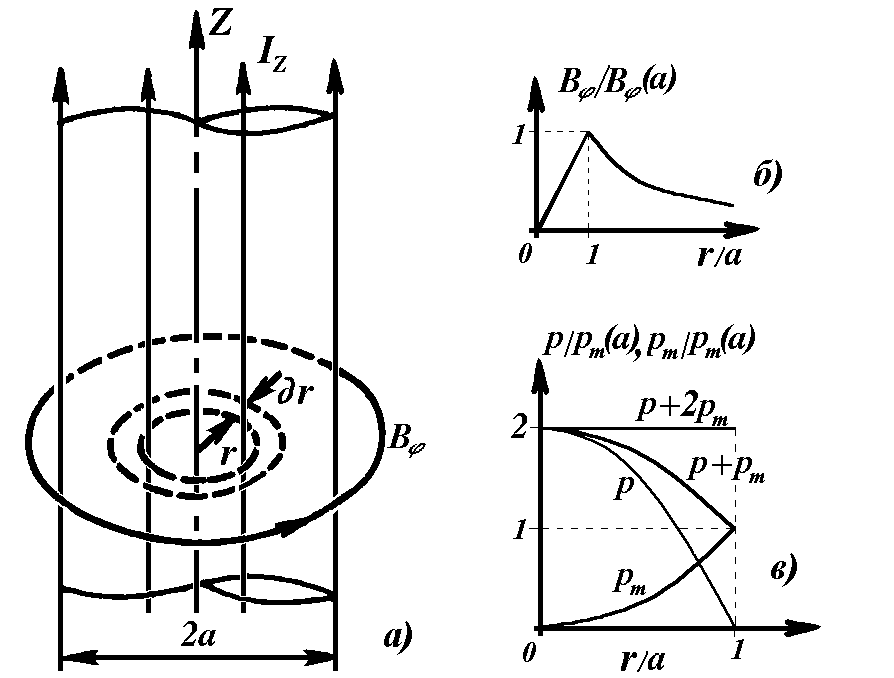
У

Рис.9.1. Плазменный Z-пинч: а  геометрия токового канала, б  распределение магнитного поля, в давления плазмы (р) и магнитного давления (p_m) по радиусу

равнение (9.3) для рассматриваемого частного случая устанавливает условие равновесного состояния системы “плазма  магнитное поле”, причем давление магнитного поля вне плазмы в равновесии должно быть больше магнитного давления внутреннего поля как раз на величину газокинетического давления плазмы, что наглядно демонстрирует идею удержания плазмы магнитным полем. Подчеркнем, что в уравнениях равновесия нет каких-либо ограничений на происхождение магнитного поля, поэтому оно может быть создано как внешними токами, так и током, протекающим по плазме. Вместе с тем условие (3.20) связывает две неизвестные величины. Поэтому для однозначного решения задачи равновесия необходимо привлекать дополнительные условия, в том числе условия поддержания тока в плазме.

Примером квазистационарного процесса может служить равновесное состояние самосжимающегося длинного цилиндрического столба плазмы с продольным током - так называемый Z-пинч^. В этом случае В и р зависят только от одной координаты - расстояния r от оси столба (рис.9.1). Уравнение равновесия примет вид:

.

Если считать ток пинча распределенным равномерно по его сечению, то j_z=const и , так как по теореме о циркуляции

,

где

 ток в цилиндре с радиусом r. Для области вне пинча, вновь воспользовавшись теоремой о циркуляции, получаем:

,

где I - полный ток пинча. Таким образом, распределение магнитного поля пинча следующее (рис. 9.1,б):

,

где

магнитное поле на границе плазмы.

Отметим попутно полезную практическую формулу для расчета величины этого поля:

.

Подстановка распределения поля в уравнение равновесия приводит к соотношению

.

Интегрируем и, учитывая, что на границе столба (при r=a) газокинетическое давление равно нулю (р=0), получаем

.

Подчеркнем, что сумма давлений магнитного поля и давления плазмы

теперь не является величиной постоянной (сравним с (9.3)). Очевидно, это связано с вкладом от натяжения силовых линий, которые здесь имеют форму окружностей с конечным радиусом кривизны. Постоянной теперь является величина

.

Вклад натяжения силовых линий приводит к тому, что давление плазмы в центре токового канала оказывается ровно вдвое больше магнитного давления на его границе. Распределение давлений в токовом канале показано на (рис. 9.1,в).

Так как p=2nT, то, вводя полное число частиц на единицу длины плазменного столба N (так называемое погонное число частиц) и считая температуру плазмы Т постоянной, определим

,

откуда получаем соотношение

,

известное как соотношение Беннета.

При выводе этого соотношения нами предполагалось, что температура плазмы постоянна. Однако проводимость реальной плазмы не бесконечна, и поэтому протекание тока будет сопровождаться выделением джоулева тепла и нагревом плазмы. Если этот процесс считать медленным, то условие равновесия можно считать, по крайней мере, приближенно справедливым. Следовательно, если при постоянном погонном числе частиц температура будет расти, то для обеспечения равновесия необходимо увеличивать ток.

К сожалению, в обсуждаемой выше геометрии разряда практически не удается довести плазменный столб до равновесного состояния, так как ряд процессов приводит к неустойчивости, и столб плазмы быстро разрушается.

Плазменный столб в Z-пинче опирается на электроды, значит вдоль столба уход частиц и потери энергии в области контакта неизбежны. Естественно желание свернуть столб плазмы в тор  создать замкнутую безэлектродную систему. Однако тороидальный виток с током стремится к расширению, потому что давление магнитного поля на внутреннюю поверхность витка больше, чем на наружную. Например, на любой участок витка ₁J действует отталкивающая сила от диаметрально противоположного участка витка ₂J (рис.9.2), поскольку, как известно, антипараллельные токи отталкиваются. Чтобы обеспечить равновесие плазменного витка, его можно было бы поместить в вертикальное магнитное поле В_z, направленное по оси z, перпендикулярной плоскости витка (плоскости рис.9.2). Тогда силы, растягивающие виток F₁J², могут быть скомпенсированы силами, сжимающими его, F₂JВ_z. Расчеты показывают, что при этом равновесие достигается, если

,

где J - полный ток в плазменном витке.

Равновесное состояние витка может быть получено также (на временах масштаба скиновых), если его поместить в хорошо проводящий металлический кожух. Смещение витка приводит к возникновению токов Фуко в кожухе, и магнитные поля этих токов играют роль поля В_z. В этом случае время существования равновесного состояния зависит от соотношения радиуса плазменного шнура a, радиуса камеры тора R, проводимости и толщины r проводящего кожуха.

Рис.9.2. Геометрия тороидального витка плазмы

Стабилизация положения плазменного витка с током вертикальным магнитным полем и проводящим массивным металлическим кожухом реально использовались в токамаках для обеспечения равновесия по большому радиусу тора. Равновесие по малому радиусу обеспечивается (в совокупности с полем тока) сильным тороидальным магнитным полем.

Магнитогидродинамический метод рассмотрения дает возможность качественно и наглядно представить условия равновесия плазменного шнура различной геометрии, а расчеты позволяют оценить необходимые соотношения макроскопических параметров.