Контрольные вопросы

1. Сформулировать основные уравнения динамики произвольного движения тел.

2. Какое движение тел называется плоским?

3. Сформулировать основные уравнения плоского движения тел.

4. Дать определение моменту инерции тела относительно произвольной оси.

5. Сформулировать закон сохранения полной механической энергии для тела, системы тел.

6. Измерения каких физических величин необходимо произвести, чтобы определить моменты инерции тел на маятнике Максвелла?

7. Измерения каких физических величин в данной лабораторной работе являются прямыми, каких — косвенными?

8. Указать возможные источники систематических погрешностей в настоящей лабораторной работе.

9. Если в результате выполнения п.9 задания настоящей лабораторной работы не удается сделать заключение об экспериментальном подтверждении закона сохранения полной механической энергии, какой вывод можно сделать?

Лабораторная работа 22(22а) изучение гироскопа

Цель: изучение свободного гироскопа и вынужденной прецессии гироскопа.

Введение

Гироскоп представляет собой массивное симметричное тело (ротор), вращающийся с большой скоростью вокруг оси симметрии. Обычно гироскоп подвешивается таким образом, что одна из точек его оси оказывается закрепленной (так называемая точка опоры гироскопа). Существуют разные способы закрепления гироскопа в одной точке. Один из них — карданов подвес (рис.22.1).

Рис.22.1

Подвес состоит из двух рамок: внутренней 1 и внешней 2. Внешняя рамка может вращаться относительно подставки 3 вокруг оси Z. Во внутренней рамке монтируются подшипники ротора 4, а она сама может вращаться относительно внешней рамки вокруг оси Y. Таким образом, ось ротора Х может занимать любое положение в пространстве. Сам гироскоп в кардановом подвесе имеет три степени свободы и может совершать любые повороты вокруг центра подвеса О (точки опоры гироскопа) — точки пересечения осей карданова подвеса.

В уравновешенном (астатическом) гироскопе центр масс гироскопа совпадает с центром подвеса О.

Если трение в подшипниках и трение ротора о воздух настолько малы, что их можно считать практически отсутствующими, то момент приложенных к гироскопу внешних сил относительно точки О равен нулю и момент импульса гироскопа остается постоянным. Такой гироскоп называется свободным. Способность сохранять неизменным направление своей оси в пространстве является одним из основных свойств свободного гироскопа.

Все явления, наблюдаемые при движении гироскопа под действием приложенных к нему внешних сил, — следствие основного закона динамики вращательного движения тел:

, (22.1)

причем момент импульса ротора гироскопа и суммарный момент внешних сил, приложенных к гироскопу, берутся относительно неподвижной точки опоры гироскопа О. В дальнейшем (и в тексте, и в рисунках) будем опускать значок О у величин и . Момент сил , приложенный к внешней рамке подвеса, вызывает вращение оси гироскопа вокруг оси внутренней рамки Y; момент ,приложенный к внутренней рамке, вызывает вращение оси гироскопа вокруг оси внешней рамки Z.

Пусть к какой-либо точке А гироскопа приложена постоянная сила ,например, подвешен небольшой грузик (рис.22.2). Момент этой силынаправлен вдоль оси Y. За время момент импульса гироскопа получит приращение

,

совпадающее по направлению с , и будет равен результирующей

,

лежащей в плоскости, перпендикулярной к оси Z. Направление вектора совпадает с новым направлением оси Х вращения гироскопа. Таким образом, ось гироскопа повернется на угол .

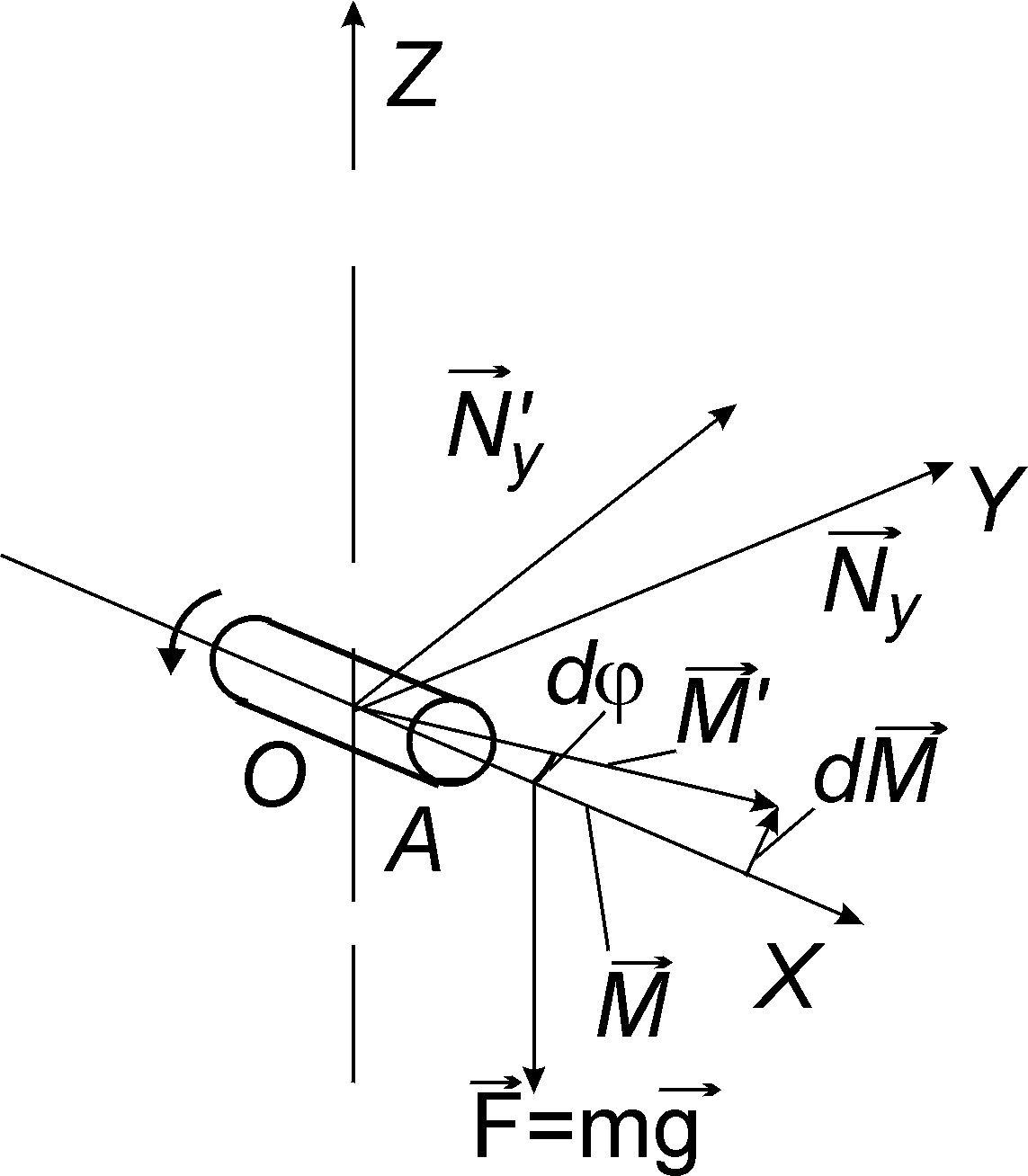
Рис.22.2

Одновременно на такой же угол повернется в плоскости хОу вектор . В результате, спустя время ,будет иметь место такое же взаимное расположение векторов и , как и в начальный момент. За последующий момент времени векторвновь получит приращение, перпендикулярное к и т.д. В итоге ось гироскопа будет поворачиваться вокруг оси Z. Такое движение гироскопа называется прецессией. Угловая скорость прецессии определяется отношением

.(22.2)

Важная особенность рассматриваемой модели гироскопа заключается в том, что момент импульса вращающегося гироскопа относительно точкиО можно с большой степенью точности положить равным его собственному моменту импульса:

,

где I — момент инерции гироскопа относительно оси Х ротора (см. введение, с. 3); — угловая скорость собственного вращения ротора гироскопа.

Это объясняется тем, что вращение гироскопа вокруг собственной оси совершается с угловой скоростью, исчисляемой тысячами оборотов в минуту, так что имеет место условие: .

В этом приближении

,(22.3)

где — поворот оси гироскопа за время.направлен по оси Z.

Подставляя (22.3) в (22.1), получим соотношение, связывающее момент внешних сил , момент импульса гироскопаи угловую скорость прецессии:

.(22.4)

Для изучения гироскопа в лаборатории есть две конструктивно различные установки (промышленная и учебная). Поэтому дальнейшее описание установок и заданий, выполняемых на этих установках, даются раздельно. В этом суть дальнейшего разделения работы на две — 22 и 22а.