Сценарии

ПРОВЕДЕНИЯ

ЛАБОРАТОРНЫХ ЗАНЯТИЙ

ЧАСТЬ 3 Работы №№ 16 - 24

Лабораторный практикум

«Механика твердого тела»

Москва 2008

С О Д Е Р Ж А Н И Е

Введение 3

Лабораторная работа 16

Определение ускорения свободного падения тел

с помощью оборотного маятника 5

Лабораторная работа 17(17а)

Изучение динамики вращательного движения физических тел 12

Лабораторная работа 18

Определение моментов инерции тел методом крутильных колебаний 33

Лабораторная работа 19

Определение эллипсоида инерции твердого тела

методом крутильных колебаний 41

Лабораторная работа 20

Изучение динамики поступательного движения тел

с помощью машины Атвуда 57

Лабораторная работа 21

Изучение динамики плоского движения физических тел 69

Лабораторная работа 22(22а)

Изучение гироскопа 79

Лабораторная работа 23

Экспериментальное определение коэффициента трения качения

с помощью наклонного маятника 95

Лабораторная работа 24

Определение скорости пули с помощью баллистического маятника 110

Основные правила работы в лаборатории кафедры общей физики 120

Измерение физических величин 123

Приложение 127

Введение

Работы, содержащиеся в данном пособии, связаны с изучением динамики вращательного движения твердого тела. Одним из центральных понятий этого раздела механики является понятие момента инерции тела относительно некоторой оси. Момент инерции тела относительно некоторой оси зависит от массы тела и распределения этой массы относительно оси. В простейшем случае материальной точки массы т момент инерции относительно произвольной оси Z равен произведению массы материальной точки на квадрат ее расстояния r до этой оси:

.

Момент инерции тела — величина аддитивная: момент инерции протяженного тела равен сумме моментов инерции его частей; момент инерции системы тел равен сумме моментов инерции отдельных тел системы. Момент инерции тела относительно произвольной оси Z определяется как сумма моментов инерции элементарных масс , на которые можно разбить тело:

,

где — расстояние от оси Z до i-й массы.

Совершив предельный переход , получим

,

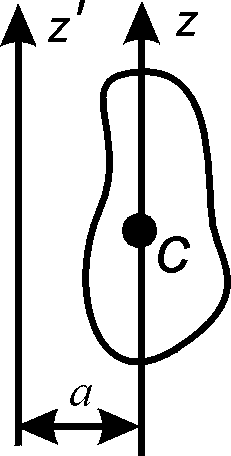
где — плотность тела, которая может изменяться в пределах тела; V — объем тела. Одно и то же тело обладает различными моментами инерции относительно разных осей. Согласно теореме Гюйгенса — Штейнера, момент инерции относительно произвольной оси равен сумме момента инерцииотносительно оси Z, параллельной данной оси Z' и проходящей через центр массы тела С, и произведения массы тела т на квадрат расстояния а между осями Z и Z' (рис.В1):

.

Рис.В1

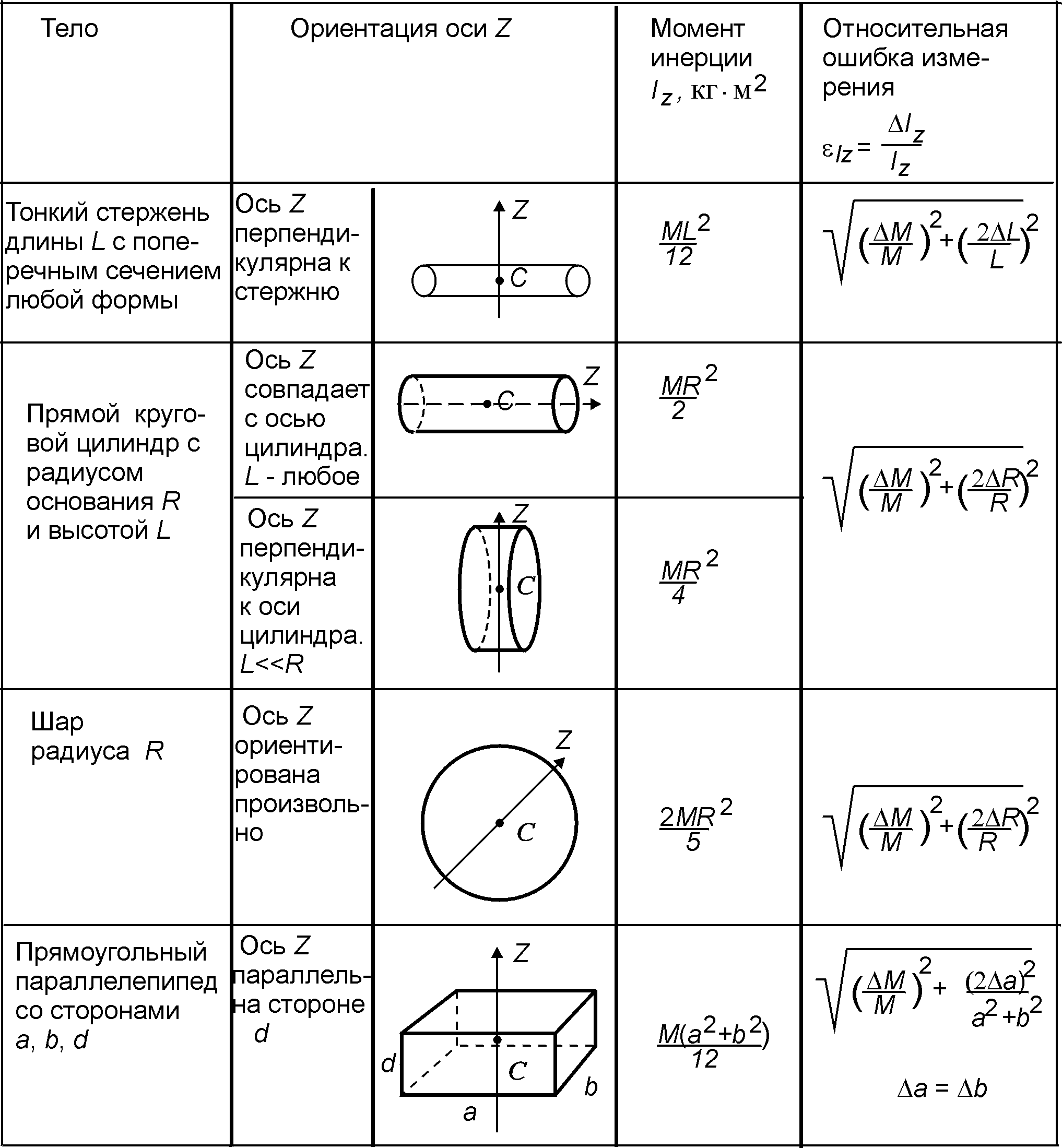
В табл.В1 приведены моменты инерции нескольких однородных (=const) тел правильной формы, использующихся в ряде лабораторных работ. Во всех случаях предполагается, что ось Z проходит через центр масс тела С и тело имеет массу М. В табл.В1 приведены также формулы для расчета погрешностей величин моментов инерции соответствующих тел. Под величинами понимаются приборные погрешности прямых измерений соответствующих величин .

Таблица В1

Предполагается, что при подготовке к выполнению лабораторной работы студент использует настоящий лабораторный практикум и первый том «Механика» курса общей физики И.В. Савельева.