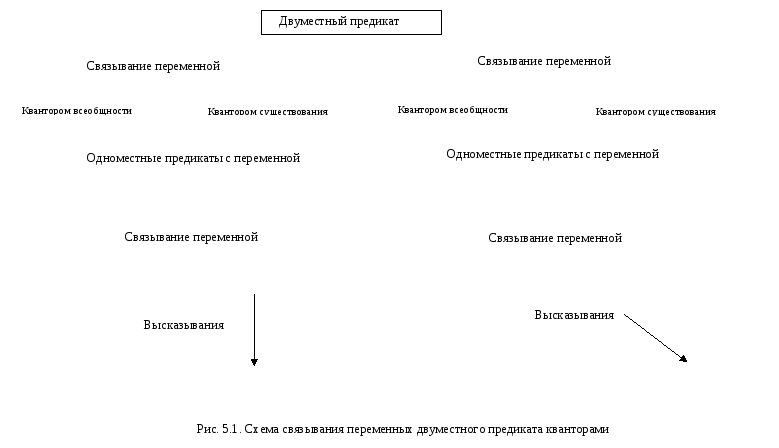
5.4. Применение языка логики предикатов в математике

Язык логики предикатов удобен для записи математических предложений. Он дает возможность выражать логические связи между понятиями, записывать определения, теоремы, доказательства.

Приведем примеры записи определений математического анализа в виде предикатных форму.

Примечание.

При записи определений используется символ "", который читается " по определению…, если… ".

1) Определение числовой последовательности:

, ("по определению число есть предел последовательности, если для любого положительного числанайдется такое натуральное число, что для всех натуральных чиселиз выполнения неравенстваследует, что"),

где ,,- член последовательности с номером, предикат– трехместный предикат, представляющий импликациюдвуместных предикатов,,.

2) Определение возрастающей функции.

Пусть . По определениюесть возрастающая на множествефункция, если, (…для любого числаиз множестваи любого числаиз этого же множества неравенствовлечет за собой неравенство).

Двуместный предикат есть импликация двуместных предикатови.

Многие теоремы математики допускают формулировку в виде условных предложений.

Примеры.

1. Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла.

2. Система линейных алгебраических уравнений имеет решение тогда и только тогда, когда ранг главной матрицы системы равен рангу ее расширенной матрицы.

3. Квадрат гипотенузы равен сумме квадратов катетов. Эту знаменитую теорему можно переформулировать так: " Для того, чтобы треугольник был прямоугольным, необходимо и достаточно, чтобы квадрат длины одной из его сторон был равен сумме квадратов длин других его сторон".

Такие формулировки являются импликациями или эквиваленциями предикатов, переменные в которых связаны кванторами.

Пусть импликация представляет условие и заключение некоторой теоремы. Рассмотрим еще три импликации, которые можно построить из предикатови:

–обратная импликация,

–противоположная импликация,

–импликация обратная противоположной.

Поскольку для эквиваленции справедливо равенство (см. табл. 5.5), то есть смысл рассматривать лишь противоположную ей эквиваленциюИз таблиц истинности импликации и эквиваленции (см. табл. 5.4, 5.5) получаем таблицы соответствующих высказываний.

Таблица 5.7 Таблица истинности импликаций и эквиваленций
0	0	1	1	1	1	1	1	1	1
0	1	1	0	1	0	0	1	0	0
1	0	0	1	0	1	1	0	0	0
1	1	0	0	1	1	1	1	1	1

Очевидны равносильности: ,(логический закон контрапозиции),,.

П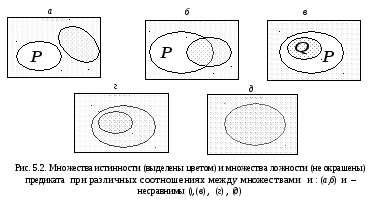усть,– множества истинности предикатовисоответственно,– множества ложности. В соответствии с таблицей истинности, импликацияложна лишь в том случае, если. Такое соотношение невозможно, если(см. рис. 5.2).

Пусть ("для любогоиз истинностиследует истинность", или "при любомистинностьявляется достаточным условием истинности") является теоремой. Назовем это утверждениипрямой теоремой. Тогда связанные с ней теоремы будут иметь следующие названия:

("для любого из истинностиследует истинность") –обратная теорема,

("для любого из ложностиследует ложность") –противоположная теорема,

("для любого из ложностиследует ложность") –теорема, обратная противоположной.

Если множество истинности условия импликации прямой теоремы есть подмножество множества истинности ее заключения, то импликация тождественно истинна во всей области определения переменных (см. рис. 5.2). Это означает, что высказываниеявляется истинным и следовательно, может быть доказано тогда и только тогда, когда.

В силу закона контрапозиции включение является также условием истинности высказыванияили, что то же самое,.

Высказывания иистинны при условии. Если же, но(см. рис 5.2г), то истинность является необходимым, но не достаточным условием истинности.

Таким образом, теорема может быть прочитана так: "при любомистинностьявляется достаточным условием истинности, а истинность– необходимым условием истинности"

Теорема будет доказана, если доказать включение. Теорема также будет доказана, если доказать включение, т.е доказать теорему, обратную противоположной. Такой метод доказательства носит название "метод от противного".

Чтобы опровергнуть теорему достаточно привести единственныйконтрпример, в котором истинность импликации нарушена. В самом деле, представив отрицание импликации конъюнктивной нормальной формой, получаем. Высказываниеистинно, если найдется хотя бы один, при котором– истина, а– ложь.

Высказывания иистинны, когда выполняются оба включенияи, т.е..

Теорема, содержащая необходимые и достаточные условия, формулируется в виде эквиваленции: . Прочитать такое высказывание можно одним из следующих способов: "при любомистинно тогда и только тогда, когда истинным является", " при любомистинностьявляется необходимым и достаточным условием истинности". Для доказательства такой теоремы приходится доказывать прямуюи обратную теоремы. Доказательство прямой теоремы, служит доказательством достаточности условия, доказательство обратной – необходимости этого условия. В силу эквивалентности теоремидоказательством необходимости и достаточности условия может являться любой из следующих вариантов:

и – доказательство прямой и обратной теорем,

и – доказательство прямой и противоположной теорем,

и – доказательство теоремы обратной и теоремы противоположной обратной,

и – доказательство теоремы противоположной и теоремы противоположной обратной.

Примеры.

1. Диагонали ромба взаимно перпендикулярны.

Переформулируем теорему в виде условного предложения: "Пусть – плоский выпуклый четырехугольник,и– отрезки. Если– ромб и,– диагонали, тоивзаимно перпендикулярны".

Первое предложение в этой формулировке является описанием множеств значений переменных: ,, где– множество плоских выпуклых четырехугольников,– множество отрезков. Это предложение называютпреамбулой теоремы.

Условие теоремы представляет собой конъюнкцию одноместного и двуместных предикатов: , где: "– ромб",: "– диагональ",: "– "диагональ". Предикатзадан на множестве. Заключение теоремы предикат: "ивзаимно перпендикулярны", заданный на множестве.

Прямая теоремаимеет вид:.

Обратная теорема:–"из перпендикулярности отрезковиследует, что они являются диагоналями ромба". Утверждение неверное, легко привести контрпример ложности импликации.

Противоположная теорема:–"если четырехугольникне является ромбом, или отрезкиине есть диагонали, тоине перпендикулярны друг другу". Утверждение неверное, легко привести контрпример, ложности импликации.

Теорема противоположная обратной:–"если отрезкиине перпендикулярны друг другу, то либо четырехугольник, диагоналями которого они являются, – не ромб, либо хотя бы один из них не является диагональю". Утверждение истинное.

Условие прямой теоремы является условием достаточным, но не является необходимым. Условие обратной теоремы является условием необходимым, но не достаточным.

2. Система линейных алгебраических уравнений имеет решение тогда и только тогда, когда ранг главной матрицы системы равен рангу ее расширенной матрицы.

Преамбула теоремы:, – матрица,– ее подматрица,–-мерный вектор столбец,– ранг матрицы,– ранг матрицы.

Введем предикаты:

: "",

: "".

Прямая теорема:, истинное высказывание,

Обратная теорема:– "если найдется вектор, такой что, то", истинное высказывание.

Противоположная теорема:– "если ранги матриц не равны, то решения системы не существует", истинное высказывание.

Теорема, обратная противоположной:– "если система не имеет решения, то ранги матриц не равны", истинное высказывание.

99